2020-2021学年北师大版九年级数学下册1.6 利用三角函数测高 教学课件(20张PPT)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册1.6 利用三角函数测高 教学课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 07:02:21 | ||
图片预览






文档简介
(共20张PPT)
1.6
测量物体的高度
1.能熟练运用解直角三角形测量物体的高度;
2.注意解题格式及细节.
学习目标:(1分钟)
(一)看P22活动一的内容,了解:
1.测倾器的构造;
2.测倾器测量倾斜角的方法步骤.
自学指导1:(2+3分钟)
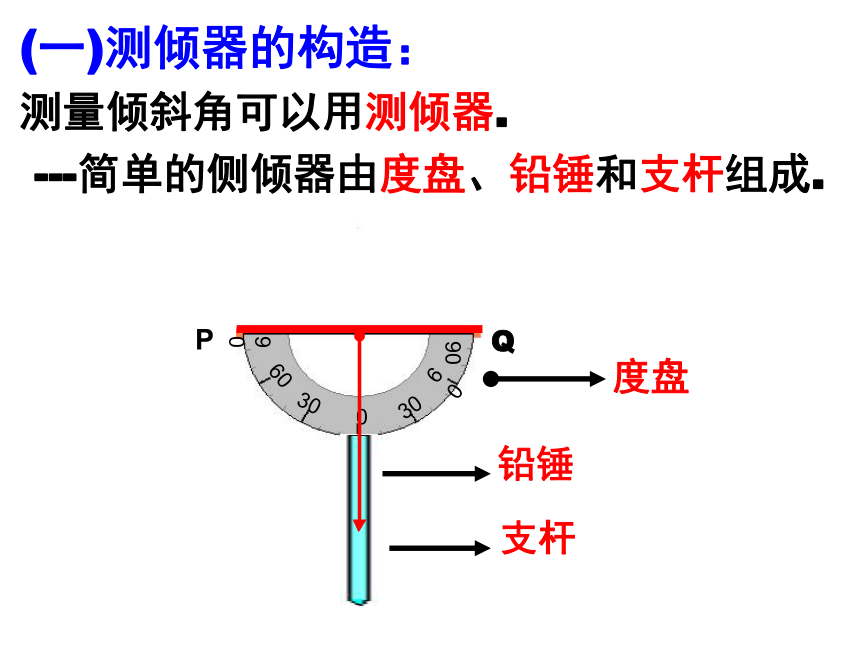
(一)测倾器的构造:
测量倾斜角可以用测倾器.
---简单的侧倾器由度盘、铅锤和支杆组成.
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
0
30
30
60
60
90
90
M
30°
P
Q
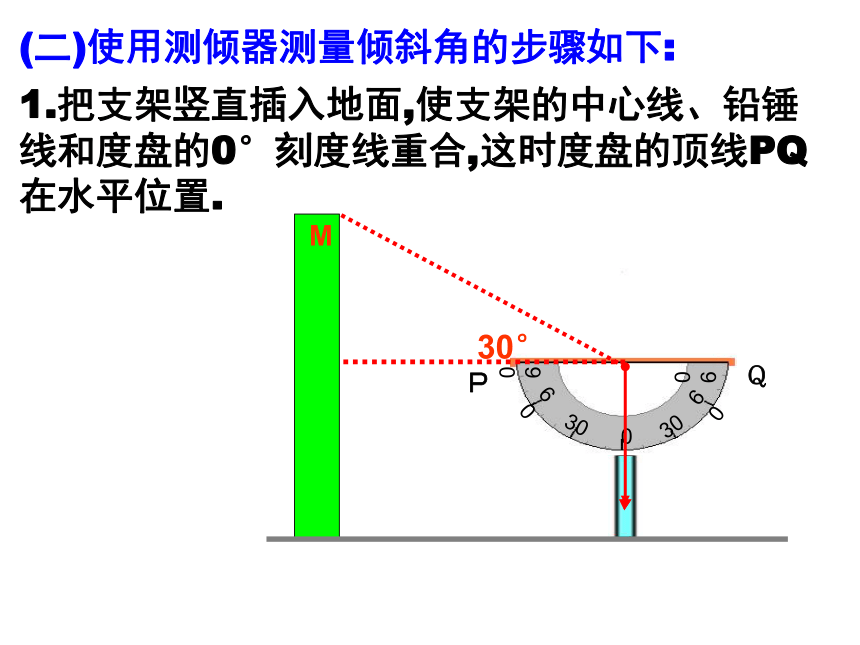
(二)使用测倾器测量倾斜角的步骤如下:
1.把支架竖直插入地面,使支架的中心线、铅锤线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
M
30°
0
30
30
60
60
90
90
P
Q
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的读数.
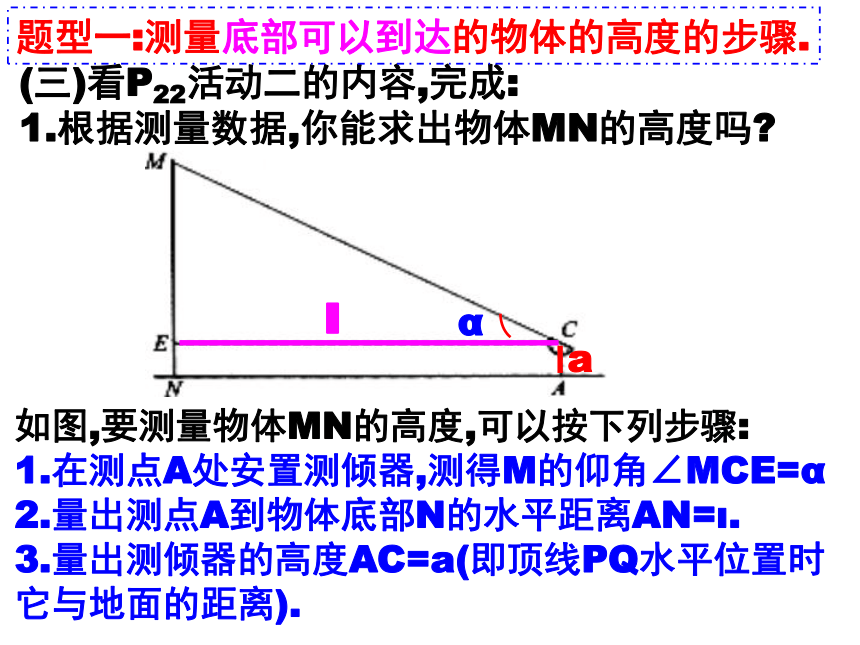
如图,要测量物体MN的高度,可以按下列步骤:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α
2.量出测点A到物体底部N的水平距离AN=ι.
3.量出测倾器的高度AC=a(即顶线PQ水平位置时它与地面的距离).
(三)看P22活动二的内容,完成:
1.根据测量数据,你能求出物体MN的高度吗?
α
ι
a
题型一:测量底部可以到达的物体的高度的步骤.
1.实践:提供选用的测量工具有:①皮尺一根;
②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪一架.请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案中,选用的测量工具是
(用工具的序号填写)
.
(2)在右图中画出你的测量方案示意图;
(3)你需要测得示意图中的哪些数据,并分别用a、b、c、
等表示测得的数据:
(4)写出求树高的算式:AB=
.
A
B
应用:测量如图所示的树的高度(底部可以到达)
a
中考连接:(6分钟)
(结果保留整数)
1.(2020?衡阳)如图,小方在五月一日假期中到郊外放风筝,风筝飞到C
处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度.
2.(2019?四川)如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
)
自学指导2:(3分钟)
题型2:测量底部不可以直接到达的物体的高度
提醒:所谓“底部不可以到达”---就是在地面上不可以直接测得测点与被测物体之间的距离.
B
D
A
C
M
N
E
α
β
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
a
b
如图,要测量物体MN的高度,可按下列步骤进行:
2.在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
1.(2019?云南)如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取
≈1.73,结果保留整数).
中考链接:(12分钟)
2.(2020?毕节)如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.
(精确到0.1米,
≈1.732)
3.(2015?山东)观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是
m.
4.(2020?钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米).
(参考数据:
1.414,
1.732)
测量底部不可以直接到达的物体的高度,如下图
测量底部可以到达的
物体的高度,如下图
小结:测量物体高度的方法有哪几种?
自学指导3:(5分钟)
例:(2019?广安)如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
中考链接:(5分钟)
1.(2019?眉山)如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:
.
(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米?
(结果保留根号)
1.6
测量物体的高度
1.能熟练运用解直角三角形测量物体的高度;
2.注意解题格式及细节.
学习目标:(1分钟)
(一)看P22活动一的内容,了解:
1.测倾器的构造;
2.测倾器测量倾斜角的方法步骤.
自学指导1:(2+3分钟)
(一)测倾器的构造:
测量倾斜角可以用测倾器.
---简单的侧倾器由度盘、铅锤和支杆组成.
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
0
30
30
60
60
90
90
M
30°
P
Q
(二)使用测倾器测量倾斜角的步骤如下:
1.把支架竖直插入地面,使支架的中心线、铅锤线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
M
30°
0
30
30
60
60
90
90
P
Q
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的读数.
如图,要测量物体MN的高度,可以按下列步骤:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α
2.量出测点A到物体底部N的水平距离AN=ι.
3.量出测倾器的高度AC=a(即顶线PQ水平位置时它与地面的距离).
(三)看P22活动二的内容,完成:
1.根据测量数据,你能求出物体MN的高度吗?
α
ι
a
题型一:测量底部可以到达的物体的高度的步骤.
1.实践:提供选用的测量工具有:①皮尺一根;
②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪一架.请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案中,选用的测量工具是
(用工具的序号填写)
.
(2)在右图中画出你的测量方案示意图;
(3)你需要测得示意图中的哪些数据,并分别用a、b、c、
等表示测得的数据:
(4)写出求树高的算式:AB=
.
A
B
应用:测量如图所示的树的高度(底部可以到达)
a
中考连接:(6分钟)
(结果保留整数)
1.(2020?衡阳)如图,小方在五月一日假期中到郊外放风筝,风筝飞到C
处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度.
2.(2019?四川)如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
)
自学指导2:(3分钟)
题型2:测量底部不可以直接到达的物体的高度
提醒:所谓“底部不可以到达”---就是在地面上不可以直接测得测点与被测物体之间的距离.
B
D
A
C
M
N
E
α
β
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
a
b
如图,要测量物体MN的高度,可按下列步骤进行:
2.在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
1.(2019?云南)如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取
≈1.73,结果保留整数).
中考链接:(12分钟)
2.(2020?毕节)如图,小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高.
(精确到0.1米,
≈1.732)
3.(2015?山东)观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是
m.
4.(2020?钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米).
(参考数据:
1.414,
1.732)
测量底部不可以直接到达的物体的高度,如下图
测量底部可以到达的
物体的高度,如下图
小结:测量物体高度的方法有哪几种?
自学指导3:(5分钟)
例:(2019?广安)如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
中考链接:(5分钟)
1.(2019?眉山)如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:
.
(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米?
(结果保留根号)
