2020-2021学年华东师大版数学七年级下册6.2.1等式的性质与方程的简单变形教案
文档属性
| 名称 | 2020-2021学年华东师大版数学七年级下册6.2.1等式的性质与方程的简单变形教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 51.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 18:54:01 | ||
图片预览


文档简介
等式的性质与方程的简单变形(教学设计)
教学目标:
通过实验,让学生直观感受等式的基本性质及方程的变形规则;
在观察思考的基础上,体会方程的两种变形及解方程的两个基本步骤;
让学生经历知识的形成过程,使学生体会到在动手的过程中可以促进动脑的能力;
激发学生浓厚的学习兴趣,培养学生独立思考、勇于探索、敢于创新的精神,同时与养成学生心中有规则,按客观规律办事的良好习惯。
教学重点:
移项法则及其应用;
系数化为1的应用。
教学难点:
解方程的两个基本步骤的熟练应用
教学过程:
通过实验,得出等式的基本性质
演示a=b
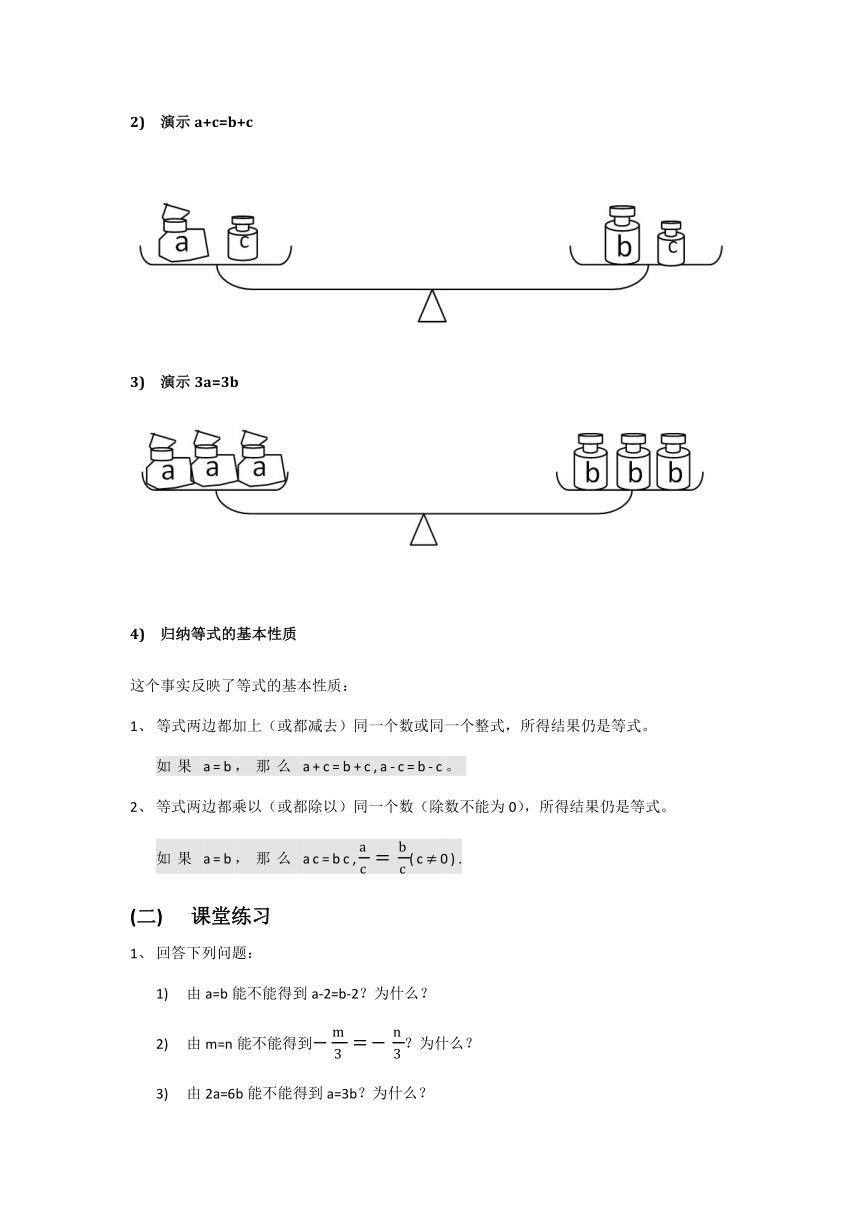
演示a+c=b+c
演示3a=3b
归纳等式的基本性质
这个事实反映了等式的基本性质:
等式两边都加上(或都减去)同一个数或同一个整式,所得结果仍是等式。
如果a=b,那么a+c=b+c,a-c=b-c。
等式两边都乘以(或都除以)同一个数(除数不能为0),所得结果仍是等式。
如果a=b,那么ac=bc,(c0).
课堂练习
回答下列问题:
由a=b能不能得到a-2=b-2?为什么?
由m=n能不能得到?为什么?
由2a=6b能不能得到a=3b?为什么?
由能不能得到3x=2y?为什么?
答案:
能,根据等式性质1,由a=b两边都减去2就能得到a-2=b-2。
能,根据等式性质2,由m=n两边都除以-3就能得到。
能,根据等式性质2,由2a=6b两边都除以2就能得到a=3b。
能,根据等式性质2,由两边都乘以6就能得到3x=2y。
填空,使所得结果仍是等式,并说明是根据哪一条等式的性质得到的:
如果x-2=5,那么x=5+
;(2)
如果3x=10-2x,那么3x+
=10;(2x)
如果2x=7,那么x=
;()
如果=3,那么x-1=
.
(6)
方程的变形规则及其应用
方程的变形规则
由等式的基本性质,可以得到方程的变形规则:
方程两边都加上(或都减去)同一个数或同一个整式,方程的解不变;
方程两边都乘以(或都除以)同一个不等于0的数,方程的解不变。
根据这些规则,我们可以对方程进行适当的变形,求得方程的解。
方程的变形规则的应用一:移项
例1
解下列方程
x-5=7
4x=3x-4
分析:因为解方程就是把方程变形为x=a的形式,所以通过观察发现x-5=7中-5是“多余”
的。经过思考,我们可以依据方程的变形规则1在方程的两边同时都加上5就可以把这个“多余”
的-5给去掉了。同理,我们也可以通过观察发现4x=3x-4发现中3x也是“多余”
的。经过思考,我们可以依据方程的变形规则1我们们在方程的两边同时减去3x就可以把这个“多余”的3x给去掉了。
解:1)x-5=7
x-5+5=7+5
x=12
2)4x=3x-4
4x-3x=3x-4-3x
X=-4
归纳总结新知识:
以上两个方程的解法,都依据了方程的变形规则1.这里的变形,相当于将方程中的某些项改变符号后,从方程的一边移到另一边。像这样的变形叫做移项。
方程的变形规则的应用二:系数化成1
例2解下列方程
-5x=2
=
分析:因为解方程就是把方程变形为x=a的形式,所以通过观察发现-5x=2
中-5是“多余”
的。经过思考,我们可以依据方程的变形规则2在方程的两边同时都除以-5就可以把这个“多余”
的-5给去掉了。同理,我们也可以通过观察发现=发现中也是“多余”
的。经过思考,我们可以依据方程的变形规则2我们们在方程的两边同时除以就可以把这个“多余”的给去掉了。
解:1)-5x=2
=
X=-
2)=
÷=÷
X=
归纳总结新知识:
这两个方程的解法,都依据了方程的变形规则2.将方程的两边都除以未知数的系数。。像这样的变形通常称作“将未知数的系数化成1”。
以上例1和例2解方程的过程,都是讲方程进行适当的变形,得到x=a的形式。
课堂练习
下列方程的变形是否正确?为什么?
由3+x=5,得x=5+3;
由7x=-4,得x=-;
由=0,得y=2;
由3=x-2,得x=-2-3
2、(口答)求下列方程的解:
x-6=6
7x=6x-4
-5x=60
本课小结
这节课,我们学习了解方程的两个基本步骤移项和将未知数的系数化成1。移项的依据是方程的变形规则1,将未知数的系数化成1的依据是方程的变形规则2。我们要在具体的做题当中去理解它们,更重要的是在实际中去熟练应用它们。
作业布置
教材第9页习题第1题
(
例题讲解区
练习讲解区
)
(
6.2.1等式的性质与方程的简单变形
等式的基本性质
如果a=b,那么a+c=b+c,a-c=b-c。
如果a=b,那么ac=bc,
(c
0)
.
方程的变形规则
由等式的基本性质,可以得到方程的变形规则:
方程两边都加上(或都减去)同一个数或同一个整式,方程的解不变;
方程两边都乘以(或都除以)同一个不等于0的数,方程的解不变。
解方程的两个基本步骤:
移项和将未知数的系数化成1
)板书设计
课后反思
经过这节课的实际讲授,我觉得前面的等式的基本性质这部分学生很好理解,加上在小学已经渗透了许多方程的知识,所以我觉得在前半部分等式的基本性质和方程的变形规则上可以压缩一下,把主要精力放在移项和将未知数的系数化成1的讲解,尤其是训练上,用以提高学生们应用的熟练程度上。
教学目标:
通过实验,让学生直观感受等式的基本性质及方程的变形规则;
在观察思考的基础上,体会方程的两种变形及解方程的两个基本步骤;
让学生经历知识的形成过程,使学生体会到在动手的过程中可以促进动脑的能力;
激发学生浓厚的学习兴趣,培养学生独立思考、勇于探索、敢于创新的精神,同时与养成学生心中有规则,按客观规律办事的良好习惯。
教学重点:
移项法则及其应用;
系数化为1的应用。
教学难点:
解方程的两个基本步骤的熟练应用
教学过程:
通过实验,得出等式的基本性质
演示a=b
演示a+c=b+c
演示3a=3b
归纳等式的基本性质
这个事实反映了等式的基本性质:
等式两边都加上(或都减去)同一个数或同一个整式,所得结果仍是等式。
如果a=b,那么a+c=b+c,a-c=b-c。
等式两边都乘以(或都除以)同一个数(除数不能为0),所得结果仍是等式。
如果a=b,那么ac=bc,(c0).
课堂练习
回答下列问题:
由a=b能不能得到a-2=b-2?为什么?
由m=n能不能得到?为什么?
由2a=6b能不能得到a=3b?为什么?
由能不能得到3x=2y?为什么?
答案:
能,根据等式性质1,由a=b两边都减去2就能得到a-2=b-2。
能,根据等式性质2,由m=n两边都除以-3就能得到。
能,根据等式性质2,由2a=6b两边都除以2就能得到a=3b。
能,根据等式性质2,由两边都乘以6就能得到3x=2y。
填空,使所得结果仍是等式,并说明是根据哪一条等式的性质得到的:
如果x-2=5,那么x=5+
;(2)
如果3x=10-2x,那么3x+
=10;(2x)
如果2x=7,那么x=
;()
如果=3,那么x-1=
.
(6)
方程的变形规则及其应用
方程的变形规则
由等式的基本性质,可以得到方程的变形规则:
方程两边都加上(或都减去)同一个数或同一个整式,方程的解不变;
方程两边都乘以(或都除以)同一个不等于0的数,方程的解不变。
根据这些规则,我们可以对方程进行适当的变形,求得方程的解。
方程的变形规则的应用一:移项
例1
解下列方程
x-5=7
4x=3x-4
分析:因为解方程就是把方程变形为x=a的形式,所以通过观察发现x-5=7中-5是“多余”
的。经过思考,我们可以依据方程的变形规则1在方程的两边同时都加上5就可以把这个“多余”
的-5给去掉了。同理,我们也可以通过观察发现4x=3x-4发现中3x也是“多余”
的。经过思考,我们可以依据方程的变形规则1我们们在方程的两边同时减去3x就可以把这个“多余”的3x给去掉了。
解:1)x-5=7
x-5+5=7+5
x=12
2)4x=3x-4
4x-3x=3x-4-3x
X=-4
归纳总结新知识:
以上两个方程的解法,都依据了方程的变形规则1.这里的变形,相当于将方程中的某些项改变符号后,从方程的一边移到另一边。像这样的变形叫做移项。
方程的变形规则的应用二:系数化成1
例2解下列方程
-5x=2
=
分析:因为解方程就是把方程变形为x=a的形式,所以通过观察发现-5x=2
中-5是“多余”
的。经过思考,我们可以依据方程的变形规则2在方程的两边同时都除以-5就可以把这个“多余”
的-5给去掉了。同理,我们也可以通过观察发现=发现中也是“多余”
的。经过思考,我们可以依据方程的变形规则2我们们在方程的两边同时除以就可以把这个“多余”的给去掉了。
解:1)-5x=2
=
X=-
2)=
÷=÷
X=
归纳总结新知识:
这两个方程的解法,都依据了方程的变形规则2.将方程的两边都除以未知数的系数。。像这样的变形通常称作“将未知数的系数化成1”。
以上例1和例2解方程的过程,都是讲方程进行适当的变形,得到x=a的形式。
课堂练习
下列方程的变形是否正确?为什么?
由3+x=5,得x=5+3;
由7x=-4,得x=-;
由=0,得y=2;
由3=x-2,得x=-2-3
2、(口答)求下列方程的解:
x-6=6
7x=6x-4
-5x=60
本课小结
这节课,我们学习了解方程的两个基本步骤移项和将未知数的系数化成1。移项的依据是方程的变形规则1,将未知数的系数化成1的依据是方程的变形规则2。我们要在具体的做题当中去理解它们,更重要的是在实际中去熟练应用它们。
作业布置
教材第9页习题第1题
(
例题讲解区
练习讲解区
)
(
6.2.1等式的性质与方程的简单变形
等式的基本性质
如果a=b,那么a+c=b+c,a-c=b-c。
如果a=b,那么ac=bc,
(c
0)
.
方程的变形规则
由等式的基本性质,可以得到方程的变形规则:
方程两边都加上(或都减去)同一个数或同一个整式,方程的解不变;
方程两边都乘以(或都除以)同一个不等于0的数,方程的解不变。
解方程的两个基本步骤:
移项和将未知数的系数化成1
)板书设计
课后反思
经过这节课的实际讲授,我觉得前面的等式的基本性质这部分学生很好理解,加上在小学已经渗透了许多方程的知识,所以我觉得在前半部分等式的基本性质和方程的变形规则上可以压缩一下,把主要精力放在移项和将未知数的系数化成1的讲解,尤其是训练上,用以提高学生们应用的熟练程度上。
