离散型随机变量的期望与方差.ppt
图片预览




文档简介
(共25张PPT)
2、离散型随机变量分布列的性质:
(1)pi≥0,i=1,2,…;
(2)p1+p2+…=1.
1、离散型随机变量的分布列
3、求离散型随机变量分布列的步骤:
①离散型随机变量ξ可能取的值为x1,x2,…,
②求ξ取每一个值xi(i=1,2,…)的概率 P(ξ=xi)=pi,
③列出分布列表
回顾旧知
1.2 离散型随机变量的期望与方差
同时分别掷骰子,各押赌注32个金币
规定谁先掷出3次“6点”就算赢对方,
赌博进行了一段时间,A赌徒已掷出了2次“6点”,
B赌友也掷出了1次“6点”,
发生意外,赌博中断。
A赌徒
B赌徒
实力相当
按3:2:1的比例混合
18
混合糖果中每一粒糖果的质量都相等
教学过程
24
36
定价为混合糖果的平均价格才合理
新 授 课
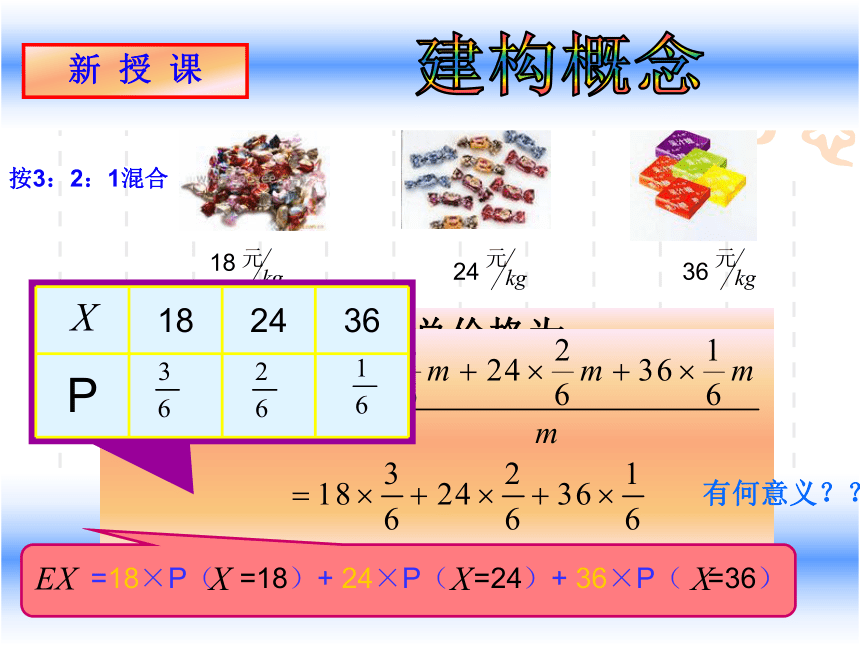
按3:2:1混合
24
36
18
教学过程
m千克混合糖果的总价格为
18× + 24× + 36×
平均价格为
18 24 36
P
=18×P( =18)+ 24×P( =24)+ 36×P( =36)
新 授 课
有何意义??
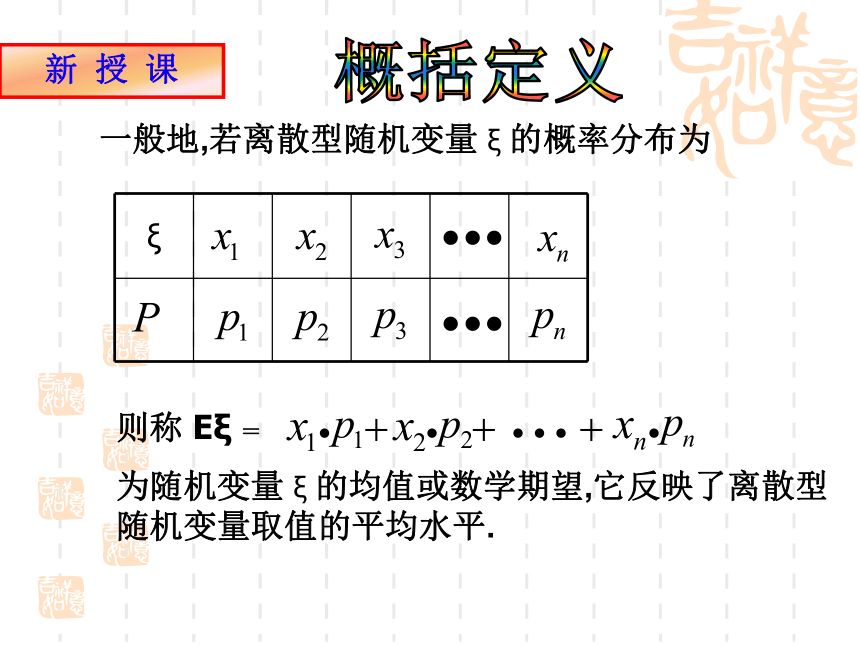
一般地,若离散型随机变量 ξ 的概率分布为
ξ
则称 Eξ =
为随机变量 ξ 的均值或数学期望,它反映了离散型随机变量取值的平均水平.
新 授 课
设η=aξ+b,其中a,b为常数,则η也是随机变量.
(1) η分布列是什么?
(2) Eη=?
问 题
新 授 课
1.2 离散型随机变量的期望与方差
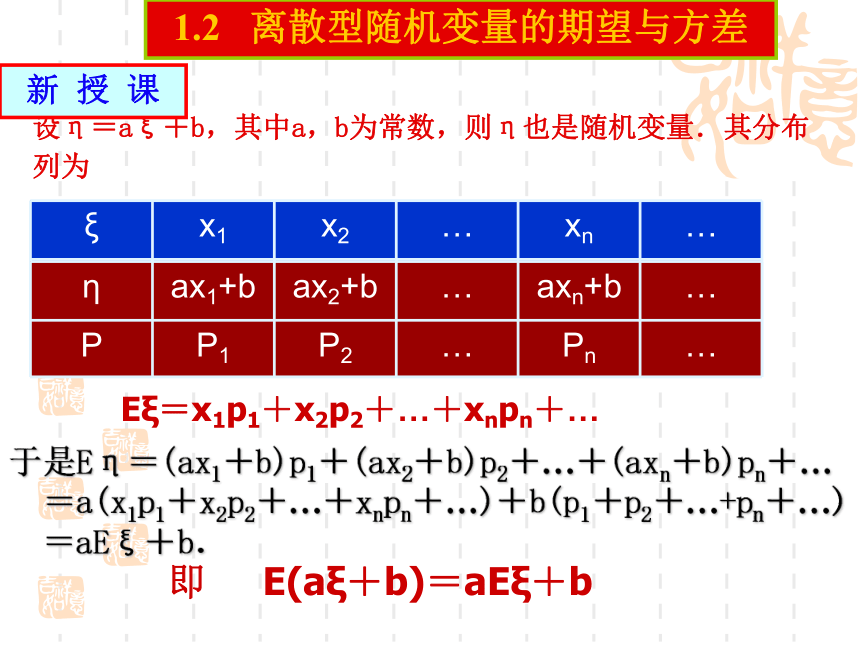
设η=aξ+b,其中a,b为常数,则η也是随机变量.其分布列为
Eξ=x1p1+x2p2+…+xnpn+…
ξ x1 x2 … xn …
η ax1+b ax2+b … axn+b …
P P1 P2 … Pn …
于是Eη=(ax1+b)p1+(ax2+b)p2+…+(axn+b)pn+…
=a(x1p1+x2p2+…+xnpn+…)+b(p1+p2+…+pn+…)
=aEξ+b.
即 E(aξ+b)=aEξ+b
η ax1+b ax2+b … axn+b …
P P1 P2 … Pn …
新 授 课
1.2 离散型随机变量的期望与方差
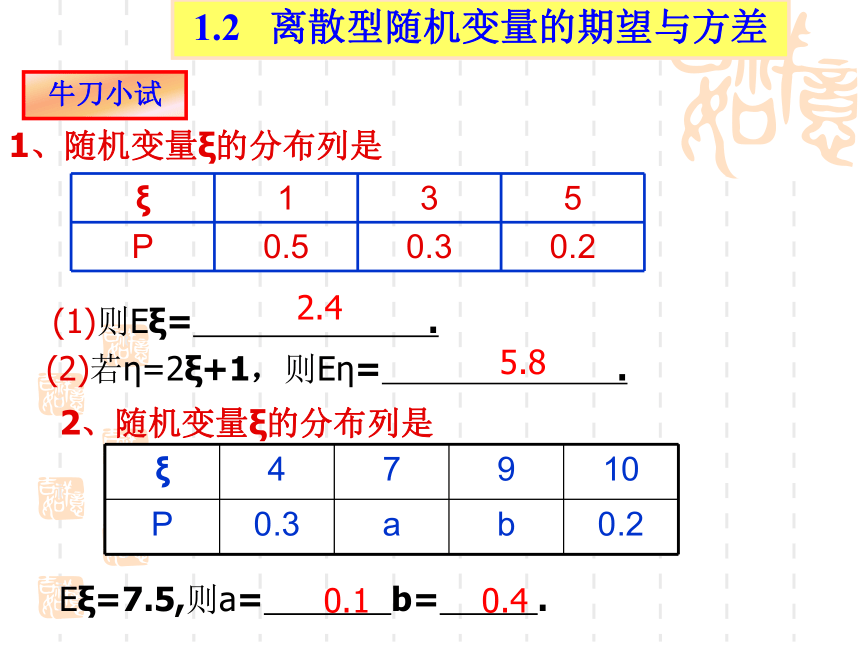
1、随机变量ξ的分布列是
ξ 1 3 5
P 0.5 0.3 0.2
(1)则Eξ= .
2、随机变量ξ的分布列是
ξ 4 a 9 10
P 0.3 0.1 b 0.2
2.4
(2)若η=2ξ+1,则Eη= .
5.8
ξ 4 7 9 10
P 0.3 a b 0.2
Eξ=7.5,则a= b= .
0.4
0.1
牛刀小试
1.2 离散型随机变量的期望与方差
1.2 离散型随机变量的期望与方差
投石问路
例1、篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,求他罚球一次的得分 的期望
解:因为 , ,所以
例2、甲、乙两名射手射击的环数为两个相互独立的随机变量X与Y ,且X ,Y的分布列为
甲、乙两名射手谁的射击水平高
X 1 2 3
P 0.3 0.1 0.6
Y 1 2 3
P 0.3 0.4 0.3
所以,甲射手比乙射手的射击水平高。
解:
投石问路
1.2 离散型随机变量的期望与方差
1.2 离散型随机变量的期望与方差
例3、随机抛掷一个骰子,求所得骰子的点数 的期望
解:投掷骰子所得点数 的概率分布为
6
5
4
3
2
1
所以
投石问路
求离散型随机变量的期望的步骤:
①离散型随机变量ξ可能取的值为x1,x2,…,
②求ξ取每一个值xi(i=1,2,…)的概率 P(ξ=xi)=pi,
③列出分布列表
④计算:Eξ=x1p1+x2p2+…+xnpn+…
1.2 离散型随机变量的期望与方差
金钥匙
1.一个袋子里装有大小相同的3 个红球和2个黄球,从中同时取2个,则其中含红球个数的数学期望是
ξ 0 1 2
P 1/10 6/10 3/10
1.2 离散型随机变量的期望与方差
快乐套餐1
2、某商场的促销决策:
统计资料表明,每年国庆节商场内促销活动可获利2万元;商场外促销活动如不遇下雨可获利10万元;如遇下雨可则损失4万元。9月30日气象预报国庆节下雨的概率为40%,商场应选择哪种促销方式?
1.2
P
10
-4
0.6
0.4
所以E =10×0.6+(-4) ×0.4=4.4
因为4.4>2,
所以商场应选择在商场外进行促销.
解:因为商场内的促销活动可获效益2万元
设商场外的促销活动可获效益 万元,则 的分布列
1.2 离散型随机变量的期望与方差
大显身手
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值
(元)的概率分布列和期望
1.2 离散型随机变量的期望与方差
大显身手
(1)
,即该顾客中奖的概率为
(2)
的所有可能值为:0,10,20,50,60(元),
,
,
故
有分布列:
1.2 离散型随机变量的期望与方差
大显身手
0 10 20 50 60
P
从而期望
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值
=2×8=16(元).
32个金币
32个金币
A已掷出了2次“6点”
B也掷出了1次“6点”
输
赢
输
赢
A的胜败
胜
败
胜
A赌赢的概率
32个金币
32个金币
64 0
P
64 0
P
A赌徒获得48个金币,B赌徒获得16个金币。
解: X,Y 分别表示A、B赌徒获得的奖金
一般地,若离散型随机变量ξ的概率分布为
则ξ的数学期望(或平均数、均值)
一、离散型随机变量取值的平均水平——数学期望
Eξ=x1p1+x2p2+…+xnpn+…
二、数学期望的性质
即 E(aξ+b)=aEξ+b
点金帚
1.2 离散型随机变量的期望与方差
2、离散型随机变量分布列的性质:
(1)pi≥0,i=1,2,…;
(2)p1+p2+…=1.
1、离散型随机变量的分布列
3、求离散型随机变量分布列的步骤:
①离散型随机变量ξ可能取的值为x1,x2,…,
②求ξ取每一个值xi(i=1,2,…)的概率 P(ξ=xi)=pi,
③列出分布列表
回顾旧知
1.2 离散型随机变量的期望与方差
同时分别掷骰子,各押赌注32个金币
规定谁先掷出3次“6点”就算赢对方,
赌博进行了一段时间,A赌徒已掷出了2次“6点”,
B赌友也掷出了1次“6点”,
发生意外,赌博中断。
A赌徒
B赌徒
实力相当
按3:2:1的比例混合
18
混合糖果中每一粒糖果的质量都相等
教学过程
24
36
定价为混合糖果的平均价格才合理
新 授 课
按3:2:1混合
24
36
18
教学过程
m千克混合糖果的总价格为
18× + 24× + 36×
平均价格为
18 24 36
P
=18×P( =18)+ 24×P( =24)+ 36×P( =36)
新 授 课
有何意义??
一般地,若离散型随机变量 ξ 的概率分布为
ξ
则称 Eξ =
为随机变量 ξ 的均值或数学期望,它反映了离散型随机变量取值的平均水平.
新 授 课
设η=aξ+b,其中a,b为常数,则η也是随机变量.
(1) η分布列是什么?
(2) Eη=?
问 题
新 授 课
1.2 离散型随机变量的期望与方差
设η=aξ+b,其中a,b为常数,则η也是随机变量.其分布列为
Eξ=x1p1+x2p2+…+xnpn+…
ξ x1 x2 … xn …
η ax1+b ax2+b … axn+b …
P P1 P2 … Pn …
于是Eη=(ax1+b)p1+(ax2+b)p2+…+(axn+b)pn+…
=a(x1p1+x2p2+…+xnpn+…)+b(p1+p2+…+pn+…)
=aEξ+b.
即 E(aξ+b)=aEξ+b
η ax1+b ax2+b … axn+b …
P P1 P2 … Pn …
新 授 课
1.2 离散型随机变量的期望与方差
1、随机变量ξ的分布列是
ξ 1 3 5
P 0.5 0.3 0.2
(1)则Eξ= .
2、随机变量ξ的分布列是
ξ 4 a 9 10
P 0.3 0.1 b 0.2
2.4
(2)若η=2ξ+1,则Eη= .
5.8
ξ 4 7 9 10
P 0.3 a b 0.2
Eξ=7.5,则a= b= .
0.4
0.1
牛刀小试
1.2 离散型随机变量的期望与方差
1.2 离散型随机变量的期望与方差
投石问路
例1、篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,求他罚球一次的得分 的期望
解:因为 , ,所以
例2、甲、乙两名射手射击的环数为两个相互独立的随机变量X与Y ,且X ,Y的分布列为
甲、乙两名射手谁的射击水平高
X 1 2 3
P 0.3 0.1 0.6
Y 1 2 3
P 0.3 0.4 0.3
所以,甲射手比乙射手的射击水平高。
解:
投石问路
1.2 离散型随机变量的期望与方差
1.2 离散型随机变量的期望与方差
例3、随机抛掷一个骰子,求所得骰子的点数 的期望
解:投掷骰子所得点数 的概率分布为
6
5
4
3
2
1
所以
投石问路
求离散型随机变量的期望的步骤:
①离散型随机变量ξ可能取的值为x1,x2,…,
②求ξ取每一个值xi(i=1,2,…)的概率 P(ξ=xi)=pi,
③列出分布列表
④计算:Eξ=x1p1+x2p2+…+xnpn+…
1.2 离散型随机变量的期望与方差
金钥匙
1.一个袋子里装有大小相同的3 个红球和2个黄球,从中同时取2个,则其中含红球个数的数学期望是
ξ 0 1 2
P 1/10 6/10 3/10
1.2 离散型随机变量的期望与方差
快乐套餐1
2、某商场的促销决策:
统计资料表明,每年国庆节商场内促销活动可获利2万元;商场外促销活动如不遇下雨可获利10万元;如遇下雨可则损失4万元。9月30日气象预报国庆节下雨的概率为40%,商场应选择哪种促销方式?
1.2
P
10
-4
0.6
0.4
所以E =10×0.6+(-4) ×0.4=4.4
因为4.4>2,
所以商场应选择在商场外进行促销.
解:因为商场内的促销活动可获效益2万元
设商场外的促销活动可获效益 万元,则 的分布列
1.2 离散型随机变量的期望与方差
大显身手
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值
(元)的概率分布列和期望
1.2 离散型随机变量的期望与方差
大显身手
(1)
,即该顾客中奖的概率为
(2)
的所有可能值为:0,10,20,50,60(元),
,
,
故
有分布列:
1.2 离散型随机变量的期望与方差
大显身手
0 10 20 50 60
P
从而期望
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值
=2×8=16(元).
32个金币
32个金币
A已掷出了2次“6点”
B也掷出了1次“6点”
输
赢
输
赢
A的胜败
胜
败
胜
A赌赢的概率
32个金币
32个金币
64 0
P
64 0
P
A赌徒获得48个金币,B赌徒获得16个金币。
解: X,Y 分别表示A、B赌徒获得的奖金
一般地,若离散型随机变量ξ的概率分布为
则ξ的数学期望(或平均数、均值)
一、离散型随机变量取值的平均水平——数学期望
Eξ=x1p1+x2p2+…+xnpn+…
二、数学期望的性质
即 E(aξ+b)=aEξ+b
点金帚
1.2 离散型随机变量的期望与方差
同课章节目录
