9.4菱形的性质与判定-2020-2021学年苏科版八年级数学下册专题复习提升训练(机构)(含答案)
文档属性
| 名称 | 9.4菱形的性质与判定-2020-2021学年苏科版八年级数学下册专题复习提升训练(机构)(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 663.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览


文档简介
专题复习提升训练卷9.4菱形的性质与判定-20-21苏科版八年级数学下册
一、选择题
1、下列性质中,菱形具有而平行四边形不一定具有( )
A.对角线互相平分 B.两组对角相等 C.对角线互相垂直 D.两组对边平行
2、若四边形ABCD为菱形,则下列结论中不一定成立的是( )
A.AC=BD B.AC⊥BD C.AB∥CD D.AB=CD
3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
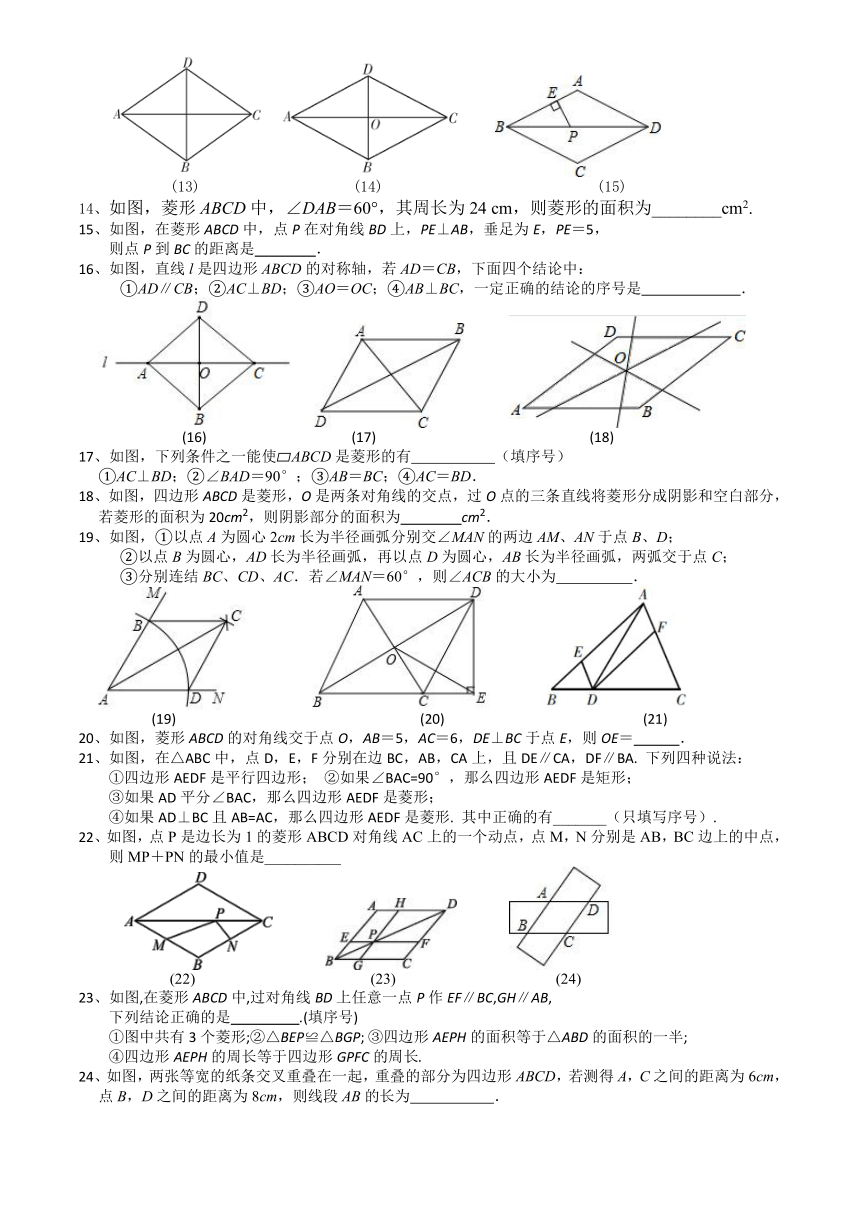
4、如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
(5) (6)
5、如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
A.4 B.8 C.16 D.24
6、如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是 ( )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
7、如图,在菱形ABCD中,AB=2,∠B=60°,E,F分别是边BC,CD的中点,则△AEF的周长为( )
A.2 B.3 C.4 D.3
(8) (9) (10)
8、如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,
∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40 B.24 C.20 D.15
9、如图所示,在?ABCD中,AE平分∠DAB交CD于点E,EF∥AD交AB于点F.若AB=9,CE=4,AE=8,
则DF的长为 ( )
A.4 B.8 C.6 D.9
10、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
11、如图,AC、BD是菱形ABCD的对角线,E、F分别是边AB、AD的中点,连接EF,EO,FO,则下列结论错误的是( )
A.EF=DO B.EF⊥AO C.四边形EOFA是菱形 D.四边形EBOF是菱形
(12)
12、如图,分别以直角三角形ABC的斜边AB,直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;
②四边形ADFE为菱形;③AD=4AG;④FH=BD.其中正确的结论是 ( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
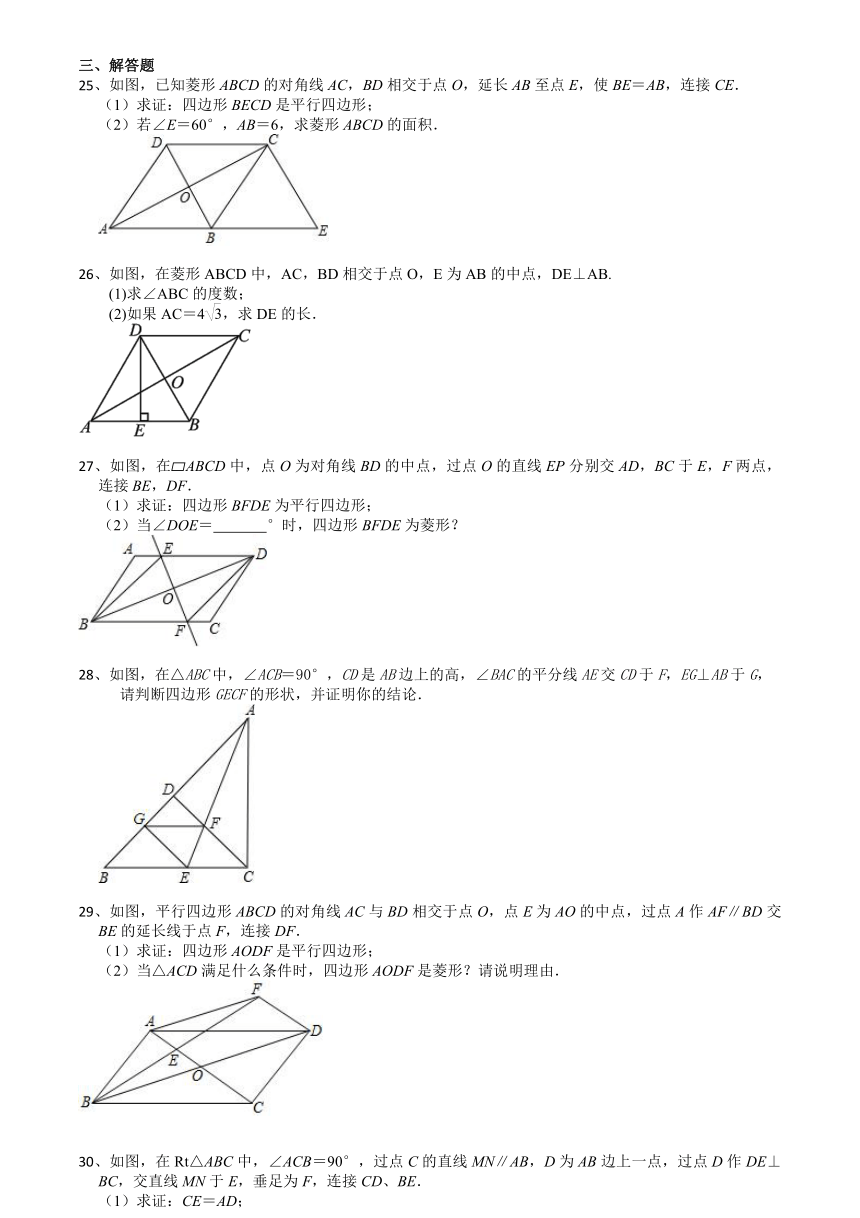
13、如图,在菱形ABCD中,若AC=8,BD=6,则菱形ABCD的面积是____.
(13) (14) (15)
14、如图,菱形ABCD中,∠DAB=60°,其周长为24 cm,则菱形的面积为________cm2.
15、如图,在菱形ABCD中,点P在对角线BD上,PE⊥AB,垂足为E,PE=5,
则点P到BC的距离是 .
16、如图,直线l是四边形ABCD的对称轴,若AD=CB,下面四个结论中:
①AD∥CB;②AC⊥BD;③AO=OC;④AB⊥BC,一定正确的结论的序号是 .
(17) (18)
17、如图,下列条件之一能使?ABCD是菱形的有 (填序号)
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
18、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm2,则阴影部分的面积为 cm2.
19、如图,①以点A为圆心2cm长为半径画弧分别交∠MAN的两边AM、AN于点B、D;
②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;
③分别连结BC、CD、AC.若∠MAN=60°,则∠ACB的大小为 .
(20) (21)
20、如图,菱形ABCD的对角线交于点O,AB=5,AC=6,DE⊥BC于点E,则OE= .
21、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA. 下列四种说法:
①四边形AEDF是平行四边形; ②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形. 其中正确的有_______(只填写序号).
22、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是__________
(23) (24)
23、如图,在菱形ABCD中,过对角线BD上任意一点P作EF∥BC,GH∥AB,
下列结论正确的是 .(填序号)
①图中共有3个菱形;②△BEP≌△BGP; ③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
24、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
三、解答题
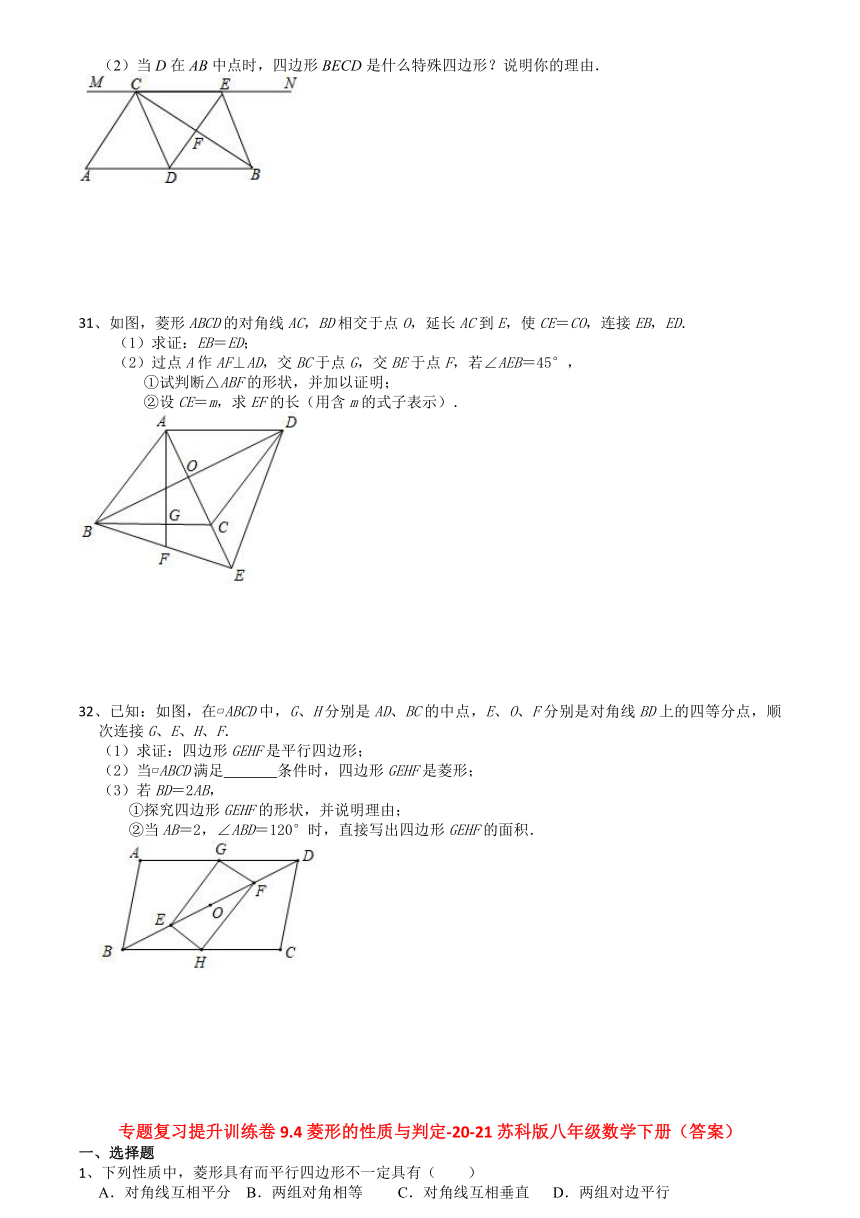
25、如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AB=6,求菱形ABCD的面积.
26、如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4,求DE的长.
27、如图,在?ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
28、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,
请判断四边形GECF的形状,并证明你的结论.
29、如图,平行四边形ABCD的对角线AC与BD相交于点O,点E为AO的中点,过点A作AF∥BD交BE的延长线于点F,连接DF.
(1)求证:四边形AODF是平行四边形;
(2)当△ACD满足什么条件时,四边形AODF是菱形?请说明理由.
30、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
31、如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
32、已知:如图,在?ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当?ABCD满足 条件时,四边形GEHF是菱形;
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由;
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
专题复习提升训练卷9.4菱形的性质与判定-20-21苏科版八年级数学下册(答案)
一、选择题
1、下列性质中,菱形具有而平行四边形不一定具有( )
A.对角线互相平分 B.两组对角相等 C.对角线互相垂直 D.两组对边平行
解:A、菱形、平行四边形的对角线互相平分,故A选项不符合题意;
B、菱形、平行四边形的两组对角分别相等,故B选项不符合题意;
C、菱形的对角线互相垂直平分,平行四边形的对角线互相平分,故C选项符合题意;
D、菱形、平行四边形的两组对边分别平行,故D选项不符合题意;
故选:C.
2、若四边形ABCD为菱形,则下列结论中不一定成立的是( )
A.AC=BD B.AC⊥BD C.AB∥CD D.AB=CD
解:如图所示:∵四边形ABCD是菱形,∴AB∥CD,AB=CD,AC⊥BD;
故选项B、C、D不符合题意;
∵菱形的对角线不一定相等, ∴AC=BD,不一定成立,故选项A符合题意;
故选:A.
3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
解:∵四边形ABCD是菱形,AC=12,BD=16,
∴菱形ABCD的面积=AC×BD=×12×16=96;
故选:C.
4、如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( A )
A.8 B.7 C.4 D.3
5、如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
A.4 B.8 C.16 D.24
解:∵四边形ABCD是菱形,∴AC⊥BD,AB=BC=CD=AD,
∵点P是AB的中点,∴AB=2OP,
∵PO=2,∴AB=4,
∴菱形ABCD的周长是:4×4=16,
故选:C.
6、如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是 (D )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
7、如图,在菱形ABCD中,AB=2,∠B=60°,E,F分别是边BC,CD的中点,则△AEF的周长为( B )
A.2 B.3 C.4 D.3
8、如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40 B.24 C.20 D.15
【解析】解:∵AB=AD,点O是BD的中点,∴AC⊥BD,∠BAO=∠DAO,
∵∠ABD=∠CDB,∴AB∥CD,∴∠BAC=∠ACD,∴∠DAC=∠ACD,
∴AD=CD,∴AB=CD,∴四边形ABCD是菱形,
∵AB=5,BO=BD=4,∴AO=3,∴AC=2AO=6,
∴四边形ABCD的面积=×6×8=24,
故选:B.
9、如图所示,在?ABCD中,AE平分∠DAB交CD于点E,EF∥AD交AB于点F.若AB=9,CE=4,AE=8,
则DF的长为 ( C )
A.4 B.8 C.6 D.9
10、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
解:∵菱形ABCD的顶点A(3,0),B(﹣2,0),∴CD=AD=AB=5,OA=3,
∴OD===4
∵AB∥CD,∴点C的坐标为(﹣5,4) 故选:D.
11、如图,AC、BD是菱形ABCD的对角线,E、F分别是边AB、AD的中点,连接EF,EO,FO,则下列结论错误的是( )
A.EF=DO B.EF⊥AO
C.四边形EOFA是菱形 D.四边形EBOF是菱形
【解析】解:∵菱形ABCD,∴BO=OD,BD⊥AC,
∵E、F分别是边AB、AD的中点,∴2EF=BD=BO+OD,EF∥BD,∴EF=DO,EF⊥AO,
∵E是AB的中点,O是BD的中点,∴2EO=AD,
同理可得:2FO=AB,
∵AB=AD,∴AE=OE=OF=AF,∴四边形EOFA是菱形,
∵AB≠BD,∴四边形EBOF是平行四边形,不是菱形,
故选:D.
12、如图,分别以直角三角形ABC的斜边AB,直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;
②四边形ADFE为菱形;③AD=4AG;④FH=BD.其中正确的结论是 ( C )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
13、如图,在菱形ABCD中,若AC=8,BD=6,则菱形ABCD的面积是__24__.
14、如图,菱形ABCD中,∠DAB=60°,其周长为24 cm,则菱形的面积为________cm2.
图8
【解析】 ∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,
∵∠DAB=60°,∴△ABD是等边三角形,
又∵周长为24 cm,即BD=AB=6 cm,
在Rt△AOD中,OD=BD=3 cm,
∴AO===3 cm,
∴AC=2AO=6,菱形的面积=AC·BD=×6×6=18 cm.
15、如图,在菱形ABCD中,点P在对角线BD上,PE⊥AB,垂足为E,PE=5,
则点P到BC的距离是 .
【解析】∵四边形ABCD是菱形,
∴BD平分∠ABC,
∵PE⊥AB,PE=5,
∴点P到BC的距离等于5,
故答案为:5.
16、如图,直线l是四边形ABCD的对称轴,若AD=CB,下面四个结论中:
①AD∥CB;②AC⊥BD;③AO=OC;④AB⊥BC,一定正确的结论的序号是 .
【解析】解:∵直线l是四边形ABCD的对称轴,∴AD=AB,CD=CB,
∵AD=BC,∴AD=CD=AB=CD,∴四边形ABCD是菱形,∴①AD∥CB,正确;
②AC⊥BD,正确;
③AO=OC,正确;
④AB不一定垂直于BC,错误.
故正确的是①②③. 故答案为:①②③.
17、如图,下列条件之一能使?ABCD是菱形的有 (填序号)
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
解:因为一组邻边相等的平行四边形是菱形;对角线互相垂直平分的四边形是菱形.
则能使?ABCD是菱形的有①或③.
18、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm2,则阴影部分的面积为 cm2.
【解析】∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,
∴△OEG≌△OFH,四边形OMAH≌四边形ONCG,四边形OEDM≌四边形OFBN,
∴阴影部分的面积=S菱形ABCD=×20=10(cm2).
故答案为:10.
19、如图,①以点A为圆心2cm长为半径画弧分别交∠MAN的两边AM、AN于点B、D;
②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;
③分别连结BC、CD、AC.若∠MAN=60°,则∠ACB的大小为 .
【解析】解:由题意可得:AB=BC=CD=AD=2cm,∴四边形ABCD是菱形,
∴BC∥DA,∠CAB=∠CAD=∠MAN=30°,
∴∠ACB=∠CAD=30°, 故答案为:30°.
20、如图,菱形ABCD的对角线交于点O,AB=5,AC=6,DE⊥BC于点E,则OE= .
【解析】∵四边形ABCD是菱形,∴AD=AB=5,AC⊥BD,AO=AC=×6=3,OB=OD,
在Rt△AOD中,由勾股定理得:OD4,
∴BD=2OD=8,
∵DE⊥BC,∴∠DEB=90°,
∵OD=OB,∴OE=BD=×8=4,
故答案为:4.
21、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA. 下列四种说法:
①四边形AEDF是平行四边形; ②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形. 其中正确的有___①②③④____(只填写序号).
22、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是______1_______
23、如图,在菱形ABCD中,过对角线BD上任意一点P作EF∥BC,GH∥AB,
下列结论正确的是 ①②④ .(填序号)
①图中共有3个菱形;②△BEP≌△BGP; ③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
24、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
【解析】解:如图,作AR⊥BC于R,AS⊥CD于S,连接AC,BD交于点O,
由题意知,AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.
∵两张纸条等宽,∴AR=AS.
∵AR?BC=AS?CD,∴BC=CD,∴平行四边形ABCD是菱形,∴AC⊥BD.
在Rt△AOB中,OA=3cm,OB=4cm,∴AB==5(cm).
故答案是:5cm.
三、解答题
25、如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AB=6,求菱形ABCD的面积.
解答:(1)证明:∵四边形ABCD是菱形,∴AB=CD=BC,AB∥CD,
又∵BE=AB,∴BE=CD,BE∥CD,∴四边形BECD是平行四边形;
(2)解:∵四边形BECD是平行四边形,∴BD∥CE,BE=CD,BD=CE,
∵四边形ABCD是菱形,∴AC⊥BD,AB=CD=6,
∴CE⊥AC,BE=AB=BC=CD=6,∴AE=AB+BE=12,
∵AC⊥CE,∴∠ACE=90°,
∵∠E=60°,∴△BCE是等边三角形,∠CAE=30°,
∴BD=CE=BC=6,AC=CE=6,
∴菱形ABCD的面积=AC?BD=×6×6=18.
26、如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4,求DE的长.
解:(1)易证△ABD为等边三角形.∴∠DAB=60°.
∵菱形ABCD的边AD∥BC,
∴∠ABC=180°-∠DAB=180°-60°=120°,即∠ABC=120°
(2)∵四边形ABCD是菱形,∴BD⊥AC于O,
AO=AC=×4=2,由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=2
27、如图,在?ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
解答:(1)证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC, ∴∠EDB=∠FBO,
在△EOD和△FOB中,, ∴△DOE≌△BOF(ASA),∴DE=BF,
又∵DE∥BF,∴四边形BFDE为平行四边形;
(2)解:∠DOE=90°时,四边形BFDE为菱形;理由如下:
由(1)得:四边形BFDE是平行四边形,
若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形; 故答案为:90.
28、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,
请判断四边形GECF的形状,并证明你的结论.
解答:四边形GECF是菱形,
证明:∵∠ACB=90°,∴AC⊥EC.
又∵EG⊥AB,AE是∠BAC的平分线,∴GE=CE.
在Rt△AEG与Rt△AEC中,,∴Rt△AEG≌Rt△AEC(HL);∴GE=EC,
∵CD是AB边上的高,∴CD⊥AB.
又∵EG⊥AB,∴EG∥CD,∴∠CFE=∠GEA.
∵Rt△AEG≌Rt△AEC,∴∠GEA=∠CEA,
∴∠CEA=∠CFE,即∠CEF=∠CFE,∴CE=CF,∴GE=EC=FC.
又∵EG∥CD,即GE∥FC,∴四边形GECF是菱形.
29、如图,平行四边形ABCD的对角线AC与BD相交于点O,点E为AO的中点,过点A作AF∥BD交BE的延长线于点F,连接DF.
(1)求证:四边形AODF是平行四边形;
(2)当△ACD满足什么条件时,四边形AODF是菱形?请说明理由.
解答:((1)证明:∵四边形ABCD是平行四边形,∴OB=OD,OA=OC,
∵AF∥BD,∴∠EAF=∠EOB,
∵点E为AO的中点,∴AE=OE,
在△AEF和△OEB中,,∴△AEF≌△OEB(ASA),∴AF=OB,∴AF=OD,
又∵AF∥OD,∴四边形AODF是平行四边形;
(2)解:△ACD是直角三角形,∠ADC=90°时,四边形AODF是菱形;理由如下:
∵∠ADC=90°,OA=OC, ∴OD=AC=OA,
∵四边形AODF是平行四边形, ∴四边形AODF是菱形.
30、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
解答:(1)证明:∵DE⊥BC,∴∠DFB=90°,
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,∴AD=BD,
∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形.
31、如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
解答:(1)证明:∵四边形ABCD是菱形,∴EA⊥BD,OB=OD,∴EB=ED
(2)解:①结论:△ABF是等腰三角形(AB=AF);
理由:∵∠AEB=45°,EO⊥OB,∴△BOE是等腰直角三角形,∴∠OBE=∠OEB=45°,
∵AG⊥BC,∴∠AGB=∠BOC=90°,∴∠GAC+∠ACB=90°,∠ACB+∠OBC=90°,
∴∠CAG=∠CBO=∠ABO,
∵∠ABF=∠ABO+∠OBE=∠ABO+45°,∠AFB=∠CAG+∠AEB=∠CAG+45°,
∴∠AFB=∠ABF,∴AB=AF,∴△ABF是等腰三角形.
②作EH⊥AF交AF的延长线于H.
由题意CE=OC=OA=m,OB=AC═OD=2m,AE=3m,AB=AF=m,
tan∠CBO=tan∠CAG==, ∴EH=m,AH=m,
∴FH=AH﹣AF=m,
在Rt△EFH中,EF===m.
32、已知:如图,在?ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当?ABCD满足 条件时,四边形GEHF是菱形;
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由;
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
解答:(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,∴E、F分别为OB、OD的中点,
∵G是AD的中点,∴GF为△AOD的中位线,∴GF∥OA,GF=OA,
同理:EH∥OC,EH=OC,∴EH=GF,EH∥GF,∴四边形GEHF是平行四边形;
(2)解:当?ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:则AG=BH,AG∥BH,∴四边形ABHG是平行四边形,∴AB∥GH,
∵AB⊥BD,∴GH⊥BD,∴GH⊥EF,∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:①四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,∴GH=AB,
∵BD=2AB,∴AB=BD=EF,∴GH=EF,∴四边形GEHF是矩形;
②作AM⊥BD于M,GN⊥BD于N,如图3所示:则AM∥GN,
∵G是AD的中点,∴GN是△ADM的中位线,∴GN=AM,
∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,
∴BM=AB=1,AM=BM=,∴GN=,
∵BD=2AB=4,∴EF=BD=2,
∴△EFG的面积=EF×GN=×2×=,
∴四边形GEHF的面积=2△EFG的面积=.
一、选择题
1、下列性质中,菱形具有而平行四边形不一定具有( )
A.对角线互相平分 B.两组对角相等 C.对角线互相垂直 D.两组对边平行
2、若四边形ABCD为菱形,则下列结论中不一定成立的是( )
A.AC=BD B.AC⊥BD C.AB∥CD D.AB=CD
3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
4、如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
(5) (6)
5、如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
A.4 B.8 C.16 D.24
6、如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是 ( )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
7、如图,在菱形ABCD中,AB=2,∠B=60°,E,F分别是边BC,CD的中点,则△AEF的周长为( )
A.2 B.3 C.4 D.3
(8) (9) (10)
8、如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,
∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40 B.24 C.20 D.15
9、如图所示,在?ABCD中,AE平分∠DAB交CD于点E,EF∥AD交AB于点F.若AB=9,CE=4,AE=8,
则DF的长为 ( )
A.4 B.8 C.6 D.9
10、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
11、如图,AC、BD是菱形ABCD的对角线,E、F分别是边AB、AD的中点,连接EF,EO,FO,则下列结论错误的是( )
A.EF=DO B.EF⊥AO C.四边形EOFA是菱形 D.四边形EBOF是菱形
(12)
12、如图,分别以直角三角形ABC的斜边AB,直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;
②四边形ADFE为菱形;③AD=4AG;④FH=BD.其中正确的结论是 ( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
13、如图,在菱形ABCD中,若AC=8,BD=6,则菱形ABCD的面积是____.
(13) (14) (15)
14、如图,菱形ABCD中,∠DAB=60°,其周长为24 cm,则菱形的面积为________cm2.
15、如图,在菱形ABCD中,点P在对角线BD上,PE⊥AB,垂足为E,PE=5,
则点P到BC的距离是 .
16、如图,直线l是四边形ABCD的对称轴,若AD=CB,下面四个结论中:
①AD∥CB;②AC⊥BD;③AO=OC;④AB⊥BC,一定正确的结论的序号是 .
(17) (18)
17、如图,下列条件之一能使?ABCD是菱形的有 (填序号)
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
18、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm2,则阴影部分的面积为 cm2.
19、如图,①以点A为圆心2cm长为半径画弧分别交∠MAN的两边AM、AN于点B、D;
②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;
③分别连结BC、CD、AC.若∠MAN=60°,则∠ACB的大小为 .
(20) (21)
20、如图,菱形ABCD的对角线交于点O,AB=5,AC=6,DE⊥BC于点E,则OE= .
21、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA. 下列四种说法:
①四边形AEDF是平行四边形; ②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形. 其中正确的有_______(只填写序号).
22、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是__________
(23) (24)
23、如图,在菱形ABCD中,过对角线BD上任意一点P作EF∥BC,GH∥AB,
下列结论正确的是 .(填序号)
①图中共有3个菱形;②△BEP≌△BGP; ③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
24、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
三、解答题
25、如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AB=6,求菱形ABCD的面积.
26、如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4,求DE的长.
27、如图,在?ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
28、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,
请判断四边形GECF的形状,并证明你的结论.
29、如图,平行四边形ABCD的对角线AC与BD相交于点O,点E为AO的中点,过点A作AF∥BD交BE的延长线于点F,连接DF.
(1)求证:四边形AODF是平行四边形;
(2)当△ACD满足什么条件时,四边形AODF是菱形?请说明理由.
30、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
31、如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
32、已知:如图,在?ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当?ABCD满足 条件时,四边形GEHF是菱形;
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由;
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
专题复习提升训练卷9.4菱形的性质与判定-20-21苏科版八年级数学下册(答案)
一、选择题
1、下列性质中,菱形具有而平行四边形不一定具有( )
A.对角线互相平分 B.两组对角相等 C.对角线互相垂直 D.两组对边平行
解:A、菱形、平行四边形的对角线互相平分,故A选项不符合题意;
B、菱形、平行四边形的两组对角分别相等,故B选项不符合题意;
C、菱形的对角线互相垂直平分,平行四边形的对角线互相平分,故C选项符合题意;
D、菱形、平行四边形的两组对边分别平行,故D选项不符合题意;
故选:C.
2、若四边形ABCD为菱形,则下列结论中不一定成立的是( )
A.AC=BD B.AC⊥BD C.AB∥CD D.AB=CD
解:如图所示:∵四边形ABCD是菱形,∴AB∥CD,AB=CD,AC⊥BD;
故选项B、C、D不符合题意;
∵菱形的对角线不一定相等, ∴AC=BD,不一定成立,故选项A符合题意;
故选:A.
3、在菱形ABCD中,AC=12,BD=16,则该菱形的面积是( )
A.10 B.40 C.96 D.192
解:∵四边形ABCD是菱形,AC=12,BD=16,
∴菱形ABCD的面积=AC×BD=×12×16=96;
故选:C.
4、如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( A )
A.8 B.7 C.4 D.3
5、如图,在菱形ABCD中,AC与BD相交于点O,点P是AB的中点,PO=2,则菱形ABCD的周长是( )
A.4 B.8 C.16 D.24
解:∵四边形ABCD是菱形,∴AC⊥BD,AB=BC=CD=AD,
∵点P是AB的中点,∴AB=2OP,
∵PO=2,∴AB=4,
∴菱形ABCD的周长是:4×4=16,
故选:C.
6、如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是 (D )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
7、如图,在菱形ABCD中,AB=2,∠B=60°,E,F分别是边BC,CD的中点,则△AEF的周长为( B )
A.2 B.3 C.4 D.3
8、如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.40 B.24 C.20 D.15
【解析】解:∵AB=AD,点O是BD的中点,∴AC⊥BD,∠BAO=∠DAO,
∵∠ABD=∠CDB,∴AB∥CD,∴∠BAC=∠ACD,∴∠DAC=∠ACD,
∴AD=CD,∴AB=CD,∴四边形ABCD是菱形,
∵AB=5,BO=BD=4,∴AO=3,∴AC=2AO=6,
∴四边形ABCD的面积=×6×8=24,
故选:B.
9、如图所示,在?ABCD中,AE平分∠DAB交CD于点E,EF∥AD交AB于点F.若AB=9,CE=4,AE=8,
则DF的长为 ( C )
A.4 B.8 C.6 D.9
10、如图,平面直角坐标系中,菱形ABCD的顶点A(3,0),B(﹣2,0),顶点D在y轴正半轴上,
则点C的坐标为( )
A.(﹣3,4) B.(﹣4,5) C.(﹣5,5) D.(﹣5,4)
解:∵菱形ABCD的顶点A(3,0),B(﹣2,0),∴CD=AD=AB=5,OA=3,
∴OD===4
∵AB∥CD,∴点C的坐标为(﹣5,4) 故选:D.
11、如图,AC、BD是菱形ABCD的对角线,E、F分别是边AB、AD的中点,连接EF,EO,FO,则下列结论错误的是( )
A.EF=DO B.EF⊥AO
C.四边形EOFA是菱形 D.四边形EBOF是菱形
【解析】解:∵菱形ABCD,∴BO=OD,BD⊥AC,
∵E、F分别是边AB、AD的中点,∴2EF=BD=BO+OD,EF∥BD,∴EF=DO,EF⊥AO,
∵E是AB的中点,O是BD的中点,∴2EO=AD,
同理可得:2FO=AB,
∵AB=AD,∴AE=OE=OF=AF,∴四边形EOFA是菱形,
∵AB≠BD,∴四边形EBOF是平行四边形,不是菱形,
故选:D.
12、如图,分别以直角三角形ABC的斜边AB,直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;
②四边形ADFE为菱形;③AD=4AG;④FH=BD.其中正确的结论是 ( C )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题
13、如图,在菱形ABCD中,若AC=8,BD=6,则菱形ABCD的面积是__24__.
14、如图,菱形ABCD中,∠DAB=60°,其周长为24 cm,则菱形的面积为________cm2.
图8
【解析】 ∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,
∵∠DAB=60°,∴△ABD是等边三角形,
又∵周长为24 cm,即BD=AB=6 cm,
在Rt△AOD中,OD=BD=3 cm,
∴AO===3 cm,
∴AC=2AO=6,菱形的面积=AC·BD=×6×6=18 cm.
15、如图,在菱形ABCD中,点P在对角线BD上,PE⊥AB,垂足为E,PE=5,
则点P到BC的距离是 .
【解析】∵四边形ABCD是菱形,
∴BD平分∠ABC,
∵PE⊥AB,PE=5,
∴点P到BC的距离等于5,
故答案为:5.
16、如图,直线l是四边形ABCD的对称轴,若AD=CB,下面四个结论中:
①AD∥CB;②AC⊥BD;③AO=OC;④AB⊥BC,一定正确的结论的序号是 .
【解析】解:∵直线l是四边形ABCD的对称轴,∴AD=AB,CD=CB,
∵AD=BC,∴AD=CD=AB=CD,∴四边形ABCD是菱形,∴①AD∥CB,正确;
②AC⊥BD,正确;
③AO=OC,正确;
④AB不一定垂直于BC,错误.
故正确的是①②③. 故答案为:①②③.
17、如图,下列条件之一能使?ABCD是菱形的有 (填序号)
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
解:因为一组邻边相等的平行四边形是菱形;对角线互相垂直平分的四边形是菱形.
则能使?ABCD是菱形的有①或③.
18、如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm2,则阴影部分的面积为 cm2.
【解析】∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,
∴△OEG≌△OFH,四边形OMAH≌四边形ONCG,四边形OEDM≌四边形OFBN,
∴阴影部分的面积=S菱形ABCD=×20=10(cm2).
故答案为:10.
19、如图,①以点A为圆心2cm长为半径画弧分别交∠MAN的两边AM、AN于点B、D;
②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;
③分别连结BC、CD、AC.若∠MAN=60°,则∠ACB的大小为 .
【解析】解:由题意可得:AB=BC=CD=AD=2cm,∴四边形ABCD是菱形,
∴BC∥DA,∠CAB=∠CAD=∠MAN=30°,
∴∠ACB=∠CAD=30°, 故答案为:30°.
20、如图,菱形ABCD的对角线交于点O,AB=5,AC=6,DE⊥BC于点E,则OE= .
【解析】∵四边形ABCD是菱形,∴AD=AB=5,AC⊥BD,AO=AC=×6=3,OB=OD,
在Rt△AOD中,由勾股定理得:OD4,
∴BD=2OD=8,
∵DE⊥BC,∴∠DEB=90°,
∵OD=OB,∴OE=BD=×8=4,
故答案为:4.
21、如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA. 下列四种说法:
①四边形AEDF是平行四边形; ②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形. 其中正确的有___①②③④____(只填写序号).
22、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是______1_______
23、如图,在菱形ABCD中,过对角线BD上任意一点P作EF∥BC,GH∥AB,
下列结论正确的是 ①②④ .(填序号)
①图中共有3个菱形;②△BEP≌△BGP; ③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
24、如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为 .
【解析】解:如图,作AR⊥BC于R,AS⊥CD于S,连接AC,BD交于点O,
由题意知,AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.
∵两张纸条等宽,∴AR=AS.
∵AR?BC=AS?CD,∴BC=CD,∴平行四边形ABCD是菱形,∴AC⊥BD.
在Rt△AOB中,OA=3cm,OB=4cm,∴AB==5(cm).
故答案是:5cm.
三、解答题
25、如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AB=6,求菱形ABCD的面积.
解答:(1)证明:∵四边形ABCD是菱形,∴AB=CD=BC,AB∥CD,
又∵BE=AB,∴BE=CD,BE∥CD,∴四边形BECD是平行四边形;
(2)解:∵四边形BECD是平行四边形,∴BD∥CE,BE=CD,BD=CE,
∵四边形ABCD是菱形,∴AC⊥BD,AB=CD=6,
∴CE⊥AC,BE=AB=BC=CD=6,∴AE=AB+BE=12,
∵AC⊥CE,∴∠ACE=90°,
∵∠E=60°,∴△BCE是等边三角形,∠CAE=30°,
∴BD=CE=BC=6,AC=CE=6,
∴菱形ABCD的面积=AC?BD=×6×6=18.
26、如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4,求DE的长.
解:(1)易证△ABD为等边三角形.∴∠DAB=60°.
∵菱形ABCD的边AD∥BC,
∴∠ABC=180°-∠DAB=180°-60°=120°,即∠ABC=120°
(2)∵四边形ABCD是菱形,∴BD⊥AC于O,
AO=AC=×4=2,由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=2
27、如图,在?ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.
(1)求证:四边形BFDE为平行四边形;
(2)当∠DOE= °时,四边形BFDE为菱形?
解答:(1)证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC, ∴∠EDB=∠FBO,
在△EOD和△FOB中,, ∴△DOE≌△BOF(ASA),∴DE=BF,
又∵DE∥BF,∴四边形BFDE为平行四边形;
(2)解:∠DOE=90°时,四边形BFDE为菱形;理由如下:
由(1)得:四边形BFDE是平行四边形,
若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形; 故答案为:90.
28、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,
请判断四边形GECF的形状,并证明你的结论.
解答:四边形GECF是菱形,
证明:∵∠ACB=90°,∴AC⊥EC.
又∵EG⊥AB,AE是∠BAC的平分线,∴GE=CE.
在Rt△AEG与Rt△AEC中,,∴Rt△AEG≌Rt△AEC(HL);∴GE=EC,
∵CD是AB边上的高,∴CD⊥AB.
又∵EG⊥AB,∴EG∥CD,∴∠CFE=∠GEA.
∵Rt△AEG≌Rt△AEC,∴∠GEA=∠CEA,
∴∠CEA=∠CFE,即∠CEF=∠CFE,∴CE=CF,∴GE=EC=FC.
又∵EG∥CD,即GE∥FC,∴四边形GECF是菱形.
29、如图,平行四边形ABCD的对角线AC与BD相交于点O,点E为AO的中点,过点A作AF∥BD交BE的延长线于点F,连接DF.
(1)求证:四边形AODF是平行四边形;
(2)当△ACD满足什么条件时,四边形AODF是菱形?请说明理由.
解答:((1)证明:∵四边形ABCD是平行四边形,∴OB=OD,OA=OC,
∵AF∥BD,∴∠EAF=∠EOB,
∵点E为AO的中点,∴AE=OE,
在△AEF和△OEB中,,∴△AEF≌△OEB(ASA),∴AF=OB,∴AF=OD,
又∵AF∥OD,∴四边形AODF是平行四边形;
(2)解:△ACD是直角三角形,∠ADC=90°时,四边形AODF是菱形;理由如下:
∵∠ADC=90°,OA=OC, ∴OD=AC=OA,
∵四边形AODF是平行四边形, ∴四边形AODF是菱形.
30、如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
解答:(1)证明:∵DE⊥BC,∴∠DFB=90°,
∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,
∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,∴AD=BD,
∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形.
31、如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
解答:(1)证明:∵四边形ABCD是菱形,∴EA⊥BD,OB=OD,∴EB=ED
(2)解:①结论:△ABF是等腰三角形(AB=AF);
理由:∵∠AEB=45°,EO⊥OB,∴△BOE是等腰直角三角形,∴∠OBE=∠OEB=45°,
∵AG⊥BC,∴∠AGB=∠BOC=90°,∴∠GAC+∠ACB=90°,∠ACB+∠OBC=90°,
∴∠CAG=∠CBO=∠ABO,
∵∠ABF=∠ABO+∠OBE=∠ABO+45°,∠AFB=∠CAG+∠AEB=∠CAG+45°,
∴∠AFB=∠ABF,∴AB=AF,∴△ABF是等腰三角形.
②作EH⊥AF交AF的延长线于H.
由题意CE=OC=OA=m,OB=AC═OD=2m,AE=3m,AB=AF=m,
tan∠CBO=tan∠CAG==, ∴EH=m,AH=m,
∴FH=AH﹣AF=m,
在Rt△EFH中,EF===m.
32、已知:如图,在?ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当?ABCD满足 条件时,四边形GEHF是菱形;
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由;
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
解答:(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,∴E、F分别为OB、OD的中点,
∵G是AD的中点,∴GF为△AOD的中位线,∴GF∥OA,GF=OA,
同理:EH∥OC,EH=OC,∴EH=GF,EH∥GF,∴四边形GEHF是平行四边形;
(2)解:当?ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:则AG=BH,AG∥BH,∴四边形ABHG是平行四边形,∴AB∥GH,
∵AB⊥BD,∴GH⊥BD,∴GH⊥EF,∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:①四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,∴GH=AB,
∵BD=2AB,∴AB=BD=EF,∴GH=EF,∴四边形GEHF是矩形;
②作AM⊥BD于M,GN⊥BD于N,如图3所示:则AM∥GN,
∵G是AD的中点,∴GN是△ADM的中位线,∴GN=AM,
∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,
∴BM=AB=1,AM=BM=,∴GN=,
∵BD=2AB=4,∴EF=BD=2,
∴△EFG的面积=EF×GN=×2×=,
∴四边形GEHF的面积=2△EFG的面积=.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
