2020-2021学年人教版七年级数学下册 课件-9.2 一元一次不等式(24张PPT)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 课件-9.2 一元一次不等式(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 07:18:34 | ||
图片预览





文档简介
(共24张PPT)
9.2
一元一次不等式
同学们,你能根据上图对话片断估计出这头大象的体重范围吗?请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
若设大象的体重为x吨,请用不等式的知识分别表示上
面两位同学所谈话的内容:
两个含相同未知数的一元一次不等式合在一起,就得到一个一元一次不等式组.
不等式组中几个不等式的解集的公共部分,叫做这个不等式组的解集.
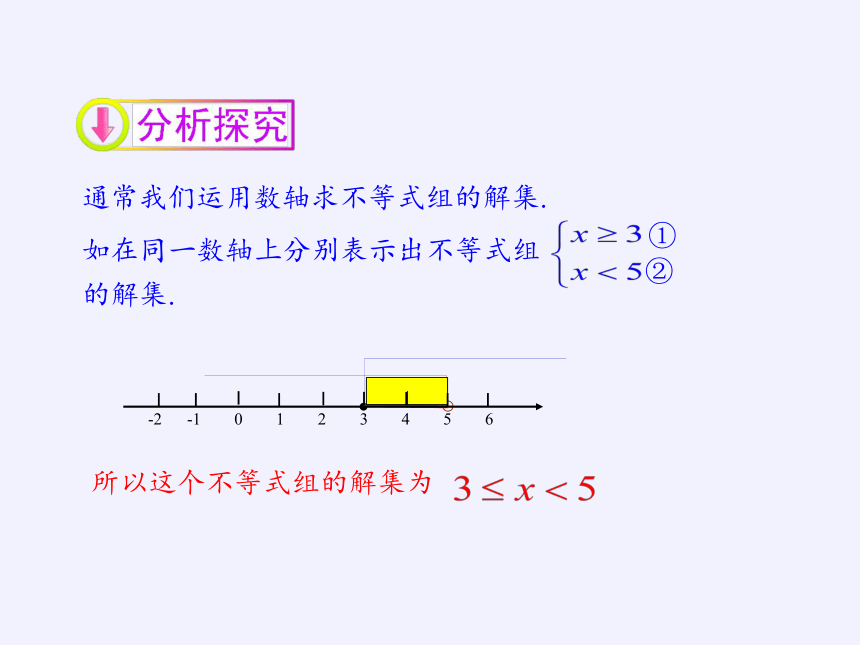
通常我们运用数轴求不等式组的解集.
②
①
如在同一数轴上分别表示出不等式组
的解集.
所以这个不等式组的解集为
-2
-1 0 1 2 3 4 5 6
例1
解不等式组
3x-1
>
2x+3
x-1<
2x+1
②
①
解:
解不等式①
,得
解不等式②
,得
x
>
4
x
>
-2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
x
>
4
(观察:数轴上解集的公共部分)
-
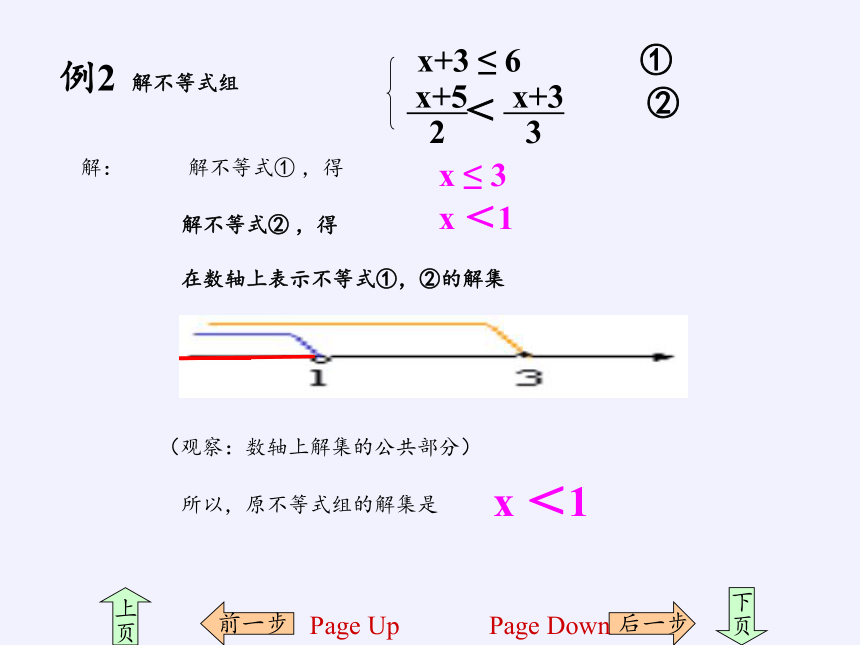
例2
解不等式组
x+3
≤
6
①
解:
解不等式①
,得
解不等式②
,得
x
≤
3
x
<1
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
(观察:数轴上解集的公共部分)
②
x
<1
x+5
2
<
x+3
3
前一步
后一步
Page
Up
Page
Down
上页
下页
例3
解不等式组
2x+3
<5
3x-2
>4
②
①
解:
解不等式①
,得
解不等式②
,得
x
<
1
x
>
2
在数轴上表示不等式①,②的解集
所以,原不等组无解
(观察:数轴上有无公共部分)
前一步
后一步
Page
Up
Page
Down
上页
下页
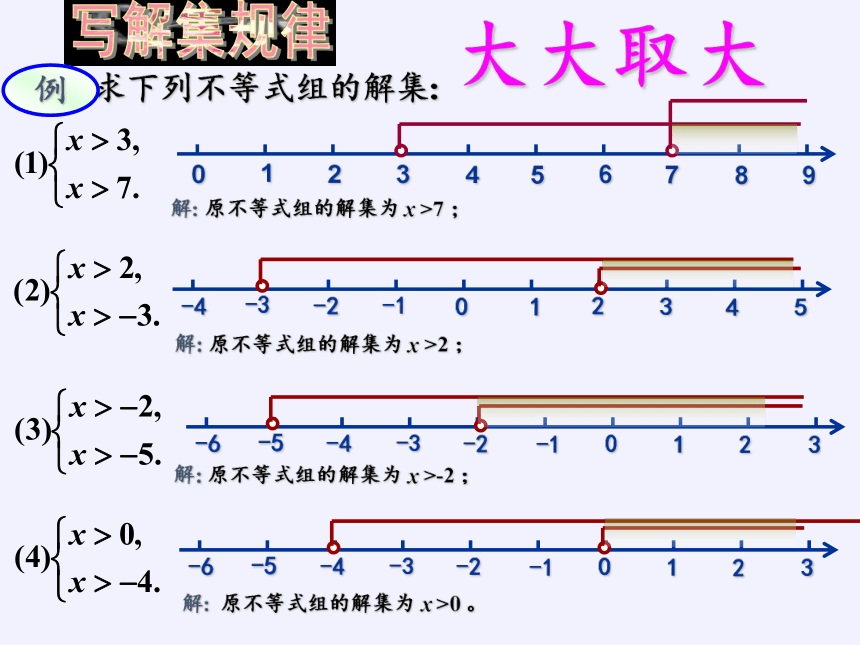
例1.
求下列不等式组的解集:
解:
原不等式组的解集为
x
>7
;
解:
原不等式组的解集为
x
>2
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解:
原不等式组的解集为
x
>-2
;
-6
1
0
-1
-2
-4
-5
-3
2
3
解:
原不等式组的解集为
x
>0
。
-6
1
0
-1
-2
-4
-5
-3
2
3
大大取大
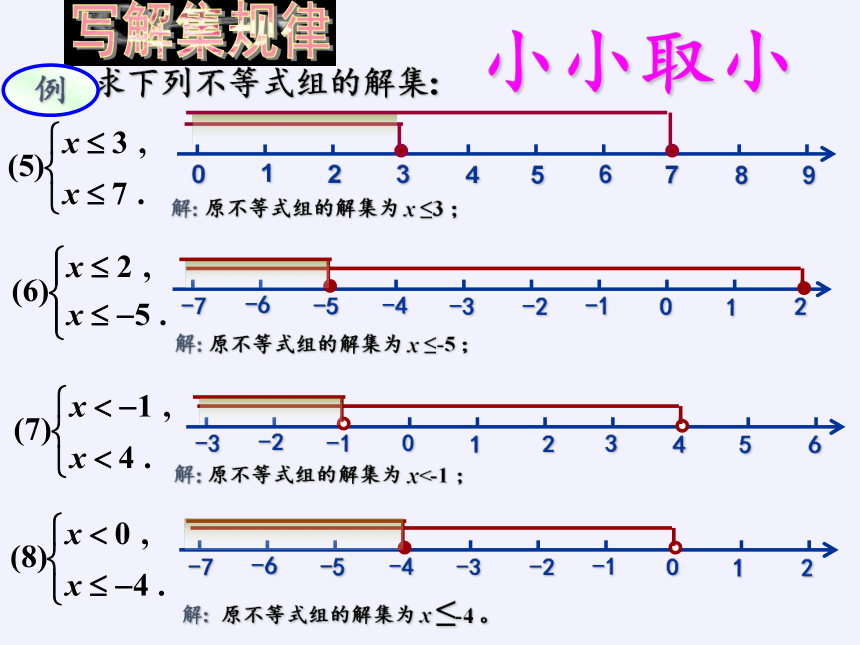
例1.
求下列不等式组的解集:
解:
原不等式组的解集为
x
≤3
;
解:
原不等式组的解集为
x
≤-5
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解:
原不等式组的解集为
x<-1
;
-3
4
3
2
1
-1
-2
0
5
6
解:
原不等式组的解集为
x
≤-4
。
-7
0
-1
-2
-3
-5
-6
-4
1
2
小小取小
例1.
求下列不等式组的解集:
解:
原不等式组的解集为
3
<
x
<
7
;
解:
原不等式组的解集为
-5<
x
<-2
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解:
原不等式组的解集为
-1≤x
<
4
;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解:
原不等式组的解集为
-4≤0
.
大小小大取中间
例1.
求下列不等式组的解集:
解:
原不等式组无解
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解:
原不等式组无解
;
解:
原不等式组无解
;
解:
原不等式组无解
;
大大小小是无解
一元一次不等式组的解集
1.大大取大
2.小小取小
3.
4.
大大
小小是无解
大小小大取中间
第一次尝试:说出下列各不等式组中,每两个不
等式解集的公共部分。
x>2
x>3
{
x<2
x<3
{
x>2
x<3
{
x<2
x>3
{
④
①
②
③
(x>3)
(x<2)
(2(无解)
例
解不等式组
5x
-2>
3x+3
①
解:
解不等式①
,得
解不等式②
,得
x
>
2.5
x
≤
4
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
2.5
<
x
≤
4
(观察:数轴上解集的公共部分)
②
x-1
≤
7
-
x
2.探究新知
40
50
用每分钟可抽30
t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1
200
t而不足
1
500
t,那么将污水抽完所用时间
x(分钟)的范围是什么?
例2、解不等式组
解:解不等式①,得x>-1
②
①
解不等式②
得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
尝试:解不列不等式组
5x
<
0
x+3
<
6
{
①
2x+3
<
5
3x-2
>
4
{
②
2x+3
≥
-1
4x-2
<
8(x+10)
{
③
x<0
无解
x
≥-2
0
8
0
2 3
你会了吗?试试看
例1:解下列不等式组
解:
解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
⑴
②
①
⑵
②
①
所以不等式组的解集:
解:
解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
0
1
2
3
4
比一比,看谁又快又好
解下列不等式组
⑴
②
①
⑵
②
①
解:解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
所以不等式的解集:
0
1
2
解:解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
所以不等式的解集:
课
后
可
要
努
力
做
练
习
!
练习一:课本129页
练习
一.练习
1.已知关于x不等式组
无解,则a的取值范围是___
a>3
2.若不等式组
无解,则m的取值范围是__________。
m
≥1.5
能
力
提
升
2、关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3
B、a≤-3
C、a>-3
D、a<-3
A
例2(1
).若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为 -1<x<2
所以, m=1
, n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1 ,
n
+
1
=
2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
谢
谢
9.2
一元一次不等式
同学们,你能根据上图对话片断估计出这头大象的体重范围吗?请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
若设大象的体重为x吨,请用不等式的知识分别表示上
面两位同学所谈话的内容:
两个含相同未知数的一元一次不等式合在一起,就得到一个一元一次不等式组.
不等式组中几个不等式的解集的公共部分,叫做这个不等式组的解集.
通常我们运用数轴求不等式组的解集.
②
①
如在同一数轴上分别表示出不等式组
的解集.
所以这个不等式组的解集为
-2
-1 0 1 2 3 4 5 6
例1
解不等式组
3x-1
>
2x+3
x-1<
2x+1
②
①
解:
解不等式①
,得
解不等式②
,得
x
>
4
x
>
-2
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
x
>
4
(观察:数轴上解集的公共部分)
-
例2
解不等式组
x+3
≤
6
①
解:
解不等式①
,得
解不等式②
,得
x
≤
3
x
<1
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
(观察:数轴上解集的公共部分)
②
x
<1
x+5
2
<
x+3
3
前一步
后一步
Page
Up
Page
Down
上页
下页
例3
解不等式组
2x+3
<5
3x-2
>4
②
①
解:
解不等式①
,得
解不等式②
,得
x
<
1
x
>
2
在数轴上表示不等式①,②的解集
所以,原不等组无解
(观察:数轴上有无公共部分)
前一步
后一步
Page
Up
Page
Down
上页
下页
例1.
求下列不等式组的解集:
解:
原不等式组的解集为
x
>7
;
解:
原不等式组的解集为
x
>2
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解:
原不等式组的解集为
x
>-2
;
-6
1
0
-1
-2
-4
-5
-3
2
3
解:
原不等式组的解集为
x
>0
。
-6
1
0
-1
-2
-4
-5
-3
2
3
大大取大
例1.
求下列不等式组的解集:
解:
原不等式组的解集为
x
≤3
;
解:
原不等式组的解集为
x
≤-5
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解:
原不等式组的解集为
x<-1
;
-3
4
3
2
1
-1
-2
0
5
6
解:
原不等式组的解集为
x
≤-4
。
-7
0
-1
-2
-3
-5
-6
-4
1
2
小小取小
例1.
求下列不等式组的解集:
解:
原不等式组的解集为
3
<
x
<
7
;
解:
原不等式组的解集为
-5<
x
<-2
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解:
原不等式组的解集为
-1≤x
<
4
;
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解:
原不等式组的解集为
-4
.
大小小大取中间
例1.
求下列不等式组的解集:
解:
原不等式组无解
;
写解集规律
例
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
-6
1
0
-1
-2
-4
-5
-3
2
3
解:
原不等式组无解
;
解:
原不等式组无解
;
解:
原不等式组无解
;
大大小小是无解
一元一次不等式组的解集
1.大大取大
2.小小取小
3.
4.
大大
小小是无解
大小小大取中间
第一次尝试:说出下列各不等式组中,每两个不
等式解集的公共部分。
x>2
x>3
{
x<2
x<3
{
x>2
x<3
{
x<2
x>3
{
④
①
②
③
(x>3)
(x<2)
(2
例
解不等式组
5x
-2>
3x+3
①
解:
解不等式①
,得
解不等式②
,得
x
>
2.5
x
≤
4
在数轴上表示不等式①,②的解集
所以,原不等式组的解集是
2.5
<
x
≤
4
(观察:数轴上解集的公共部分)
②
x-1
≤
7
-
x
2.探究新知
40
50
用每分钟可抽30
t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1
200
t而不足
1
500
t,那么将污水抽完所用时间
x(分钟)的范围是什么?
例2、解不等式组
解:解不等式①,得x>-1
②
①
解不等式②
得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
尝试:解不列不等式组
5x
<
0
x+3
<
6
{
①
2x+3
<
5
3x-2
>
4
{
②
2x+3
≥
-1
4x-2
<
8(x+10)
{
③
x<0
无解
x
≥-2
0
8
0
2 3
你会了吗?试试看
例1:解下列不等式组
解:
解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
⑴
②
①
⑵
②
①
所以不等式组的解集:
解:
解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解。
0
1
2
3
4
比一比,看谁又快又好
解下列不等式组
⑴
②
①
⑵
②
①
解:解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
所以不等式的解集:
0
1
2
解:解不等式①,得,
解不等式②,得,
把不等式①和
②的解集在数轴上表示出来:
所以不等式的解集:
课
后
可
要
努
力
做
练
习
!
练习一:课本129页
练习
一.练习
1.已知关于x不等式组
无解,则a的取值范围是___
a>3
2.若不等式组
无解,则m的取值范围是__________。
m
≥1.5
能
力
提
升
2、关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3
B、a≤-3
C、a>-3
D、a<-3
A
例2(1
).若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为 -1<x<2
所以, m=1
, n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1 ,
n
+
1
=
2
这里是一个含x的一元一次不等式组,将m,n看作两个已知数,求不等式的解集
谢
谢
