贵州省施秉县第二中学2020--2021学年度第二学期九年级开学检测试卷(word版无答案)
文档属性
| 名称 | 贵州省施秉县第二中学2020--2021学年度第二学期九年级开学检测试卷(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 150.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 00:00:00 | ||
图片预览

文档简介
九年级数学(下)施秉二中2020—2021学年度第二学期开学检测试卷
班级
学号
姓名
得分
一、选择题(每小题4分,共40分)
1.下列运算正确的是(
)
A.
(a3)4=a12
B.
a3·a4=a12
C.
a2·a2=a4
D.
(ab)2=ab2
2.某学校九年级1班九名同学参加定点投篮测试.每人投篮六次,投中的次数统计如下:
4,3,5,5,3,2,5,4,1.这组数据的中位数、众数分别为(
)
A.
4,5
B.
5,4
C.
4,4
D.
5,5
3.如图,正六边形ABCDEF内接于于⊙O,连接BD,则∠CBD的度数是(
)
A.
300
B.
450
C.
600
D.
900
4.圆锥的底面半径是5cm,侧面展开图的圆心角是1800
,圆锥的高是(
)
A.
cm
B.
10cm
C.
6cm
D.
5cm
5.若点A(-4,y1),B(-2,y2),C(2,y3)都在反比例函数
的图像上,则y1,
y2,
y3的大小关系是(
)
A.
y1>
y2>
y3
B.
y3>
y2>
y1
C.
y2>
y1>
y3
D.
y1>
y3>
y2
6.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为(
)
A.
B.
C.
D.
7.如图,小颖在围棋盘两个格点上任意摆放黑、白两个棋子,且两个棋子不在同一条网格线上,其中恰好摆放成如图所示位置的概率是(
)
A.
B.
C.
D.
8.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F.连接PB,PD,若AE=2,PF=8.则图中阴影部分的面积为(
)
A.
10
B.
12
C.
16
D.
18
9.已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图像沿x轴翻折到x轴的下方,图像的其余部分不变,得到一个新图像(如图所示).当直线y=-x+m与新图像有4个交点时,m的取值范围是(
)
A.
B.
C.
D.
10.
已知二次函数y=ax2+bx+c的图像与x轴分别交于A、B两点,与y轴交于C点,OA=OC,则由抛物线的特征写出如下结论:①abc>0
②
4ac-b2>0
③
a-b+c>0
④ac+b+1=0.其中正确的个数是(
)
A.
4个
B.
3个
C.
2个
D.
1个
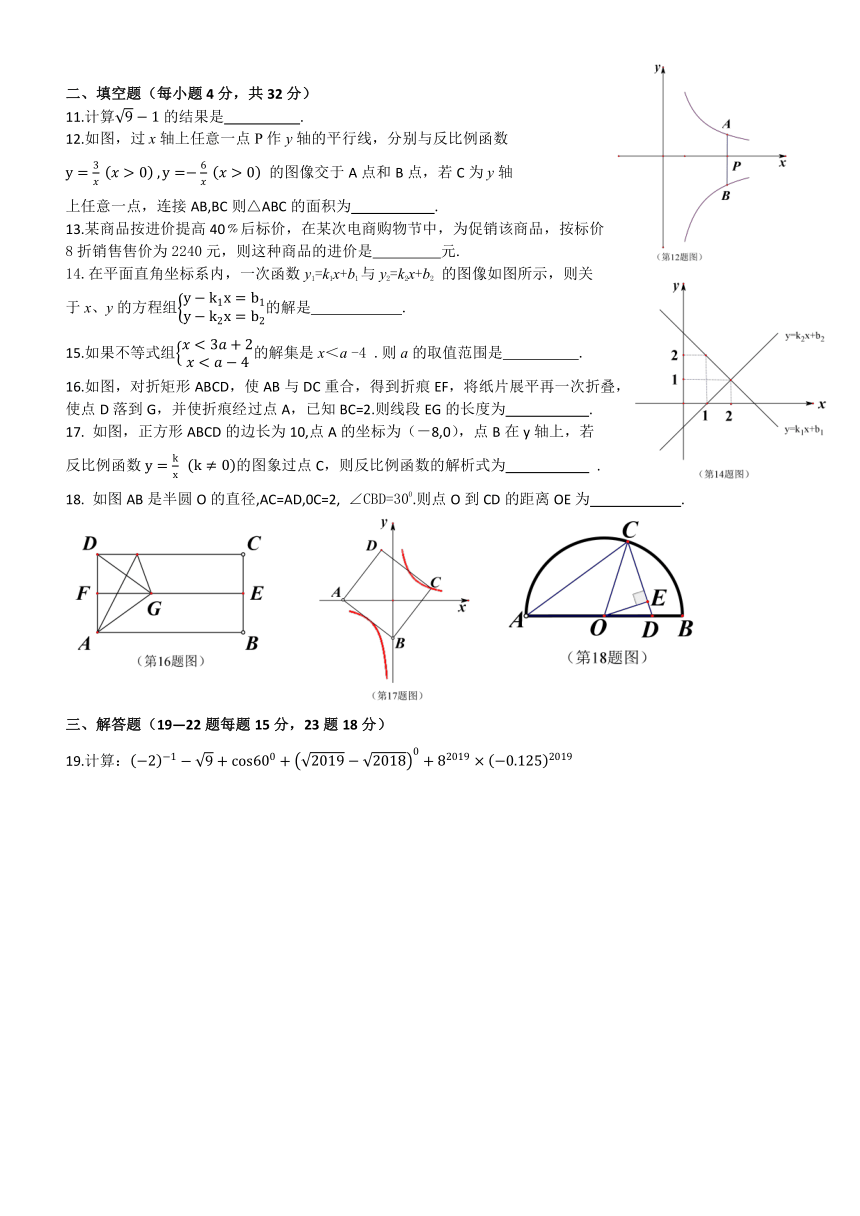
二、填空题(每小题4分,共32分)
11.计算的结果是
.
12.如图,过x轴上任意一点P作y轴的平行线,分别与反比例函数
的图像交于A点和B点,若C为y轴
上任意一点,连接AB,BC则△ABC的面积为
.
13.某商品按进价提高40﹪后标价,在某次电商购物节中,为促销该商品,按标价
8折销售售价为2240元,则这种商品的进价是
元.
14.在平面直角坐标系内,一次函数y1=k1x+b1与y2=k2x+b2
的图像如图所示,则关
于x、y的方程组的解是
.
15.如果不等式组的解集是x<a
-4
.则a的取值范围是
.
16.如图,对折矩形ABCD,使AB与DC重合,得到折痕EF,将纸片展平再一次折叠,
使点D落到G,并使折痕经过点A,已知BC=2.则线段EG的长度为
.
17.
如图,正方形ABCD的边长为10,点A的坐标为(-8,0),点B在y轴上,若
反比例函数的图象过点C,则反比例函数的解析式为
.
18.
如图AB是半圆O的直径,AC=AD,0C=2,
∠CBD=300.则点O到CD的距离OE为
.
三、解答题(19—22题每题15分,23题18分)
19.计算:
20.先化简
,再从不等式组
的整数解中选一个合适的x的值代入求值.
21.
如图,有一铁塔A、B,为了测量其高度,在水平面选取C、D两点,在C处测得A的仰角为45度,距C点10米D处测得A的仰角为60度,且C、D、B在同一水平直线上.求铁塔AB的高(结果精确到0.1米,).
22.如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过C点作⊙O的切线,交AP的延长线于点D,∠P=900,DP=1,求⊙O的直径.
23.
如图,抛物线与直线分别交于A、B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(-3,0)
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点,使|MB-MC|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA,交y轴于点Q,问是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似.若存在,求出所有符合条件的点P;若不存在,请说明理由。
班级
学号
姓名
得分
一、选择题(每小题4分,共40分)
1.下列运算正确的是(
)
A.
(a3)4=a12
B.
a3·a4=a12
C.
a2·a2=a4
D.
(ab)2=ab2
2.某学校九年级1班九名同学参加定点投篮测试.每人投篮六次,投中的次数统计如下:
4,3,5,5,3,2,5,4,1.这组数据的中位数、众数分别为(
)
A.
4,5
B.
5,4
C.
4,4
D.
5,5
3.如图,正六边形ABCDEF内接于于⊙O,连接BD,则∠CBD的度数是(
)
A.
300
B.
450
C.
600
D.
900
4.圆锥的底面半径是5cm,侧面展开图的圆心角是1800
,圆锥的高是(
)
A.
cm
B.
10cm
C.
6cm
D.
5cm
5.若点A(-4,y1),B(-2,y2),C(2,y3)都在反比例函数
的图像上,则y1,
y2,
y3的大小关系是(
)
A.
y1>
y2>
y3
B.
y3>
y2>
y1
C.
y2>
y1>
y3
D.
y1>
y3>
y2
6.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为(
)
A.
B.
C.
D.
7.如图,小颖在围棋盘两个格点上任意摆放黑、白两个棋子,且两个棋子不在同一条网格线上,其中恰好摆放成如图所示位置的概率是(
)
A.
B.
C.
D.
8.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F.连接PB,PD,若AE=2,PF=8.则图中阴影部分的面积为(
)
A.
10
B.
12
C.
16
D.
18
9.已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图像沿x轴翻折到x轴的下方,图像的其余部分不变,得到一个新图像(如图所示).当直线y=-x+m与新图像有4个交点时,m的取值范围是(
)
A.
B.
C.
D.
10.
已知二次函数y=ax2+bx+c的图像与x轴分别交于A、B两点,与y轴交于C点,OA=OC,则由抛物线的特征写出如下结论:①abc>0
②
4ac-b2>0
③
a-b+c>0
④ac+b+1=0.其中正确的个数是(
)
A.
4个
B.
3个
C.
2个
D.
1个
二、填空题(每小题4分,共32分)
11.计算的结果是
.
12.如图,过x轴上任意一点P作y轴的平行线,分别与反比例函数
的图像交于A点和B点,若C为y轴
上任意一点,连接AB,BC则△ABC的面积为
.
13.某商品按进价提高40﹪后标价,在某次电商购物节中,为促销该商品,按标价
8折销售售价为2240元,则这种商品的进价是
元.
14.在平面直角坐标系内,一次函数y1=k1x+b1与y2=k2x+b2
的图像如图所示,则关
于x、y的方程组的解是
.
15.如果不等式组的解集是x<a
-4
.则a的取值范围是
.
16.如图,对折矩形ABCD,使AB与DC重合,得到折痕EF,将纸片展平再一次折叠,
使点D落到G,并使折痕经过点A,已知BC=2.则线段EG的长度为
.
17.
如图,正方形ABCD的边长为10,点A的坐标为(-8,0),点B在y轴上,若
反比例函数的图象过点C,则反比例函数的解析式为
.
18.
如图AB是半圆O的直径,AC=AD,0C=2,
∠CBD=300.则点O到CD的距离OE为
.
三、解答题(19—22题每题15分,23题18分)
19.计算:
20.先化简
,再从不等式组
的整数解中选一个合适的x的值代入求值.
21.
如图,有一铁塔A、B,为了测量其高度,在水平面选取C、D两点,在C处测得A的仰角为45度,距C点10米D处测得A的仰角为60度,且C、D、B在同一水平直线上.求铁塔AB的高(结果精确到0.1米,).
22.如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过C点作⊙O的切线,交AP的延长线于点D,∠P=900,DP=1,求⊙O的直径.
23.
如图,抛物线与直线分别交于A、B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(-3,0)
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点,使|MB-MC|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA,交y轴于点Q,问是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似.若存在,求出所有符合条件的点P;若不存在,请说明理由。
同课章节目录
