2020-2021学年华东师大版九年级下册数学第26章 二次函数单元测试卷(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年华东师大版九年级下册数学第26章 二次函数单元测试卷(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 22:09:29 | ||
图片预览

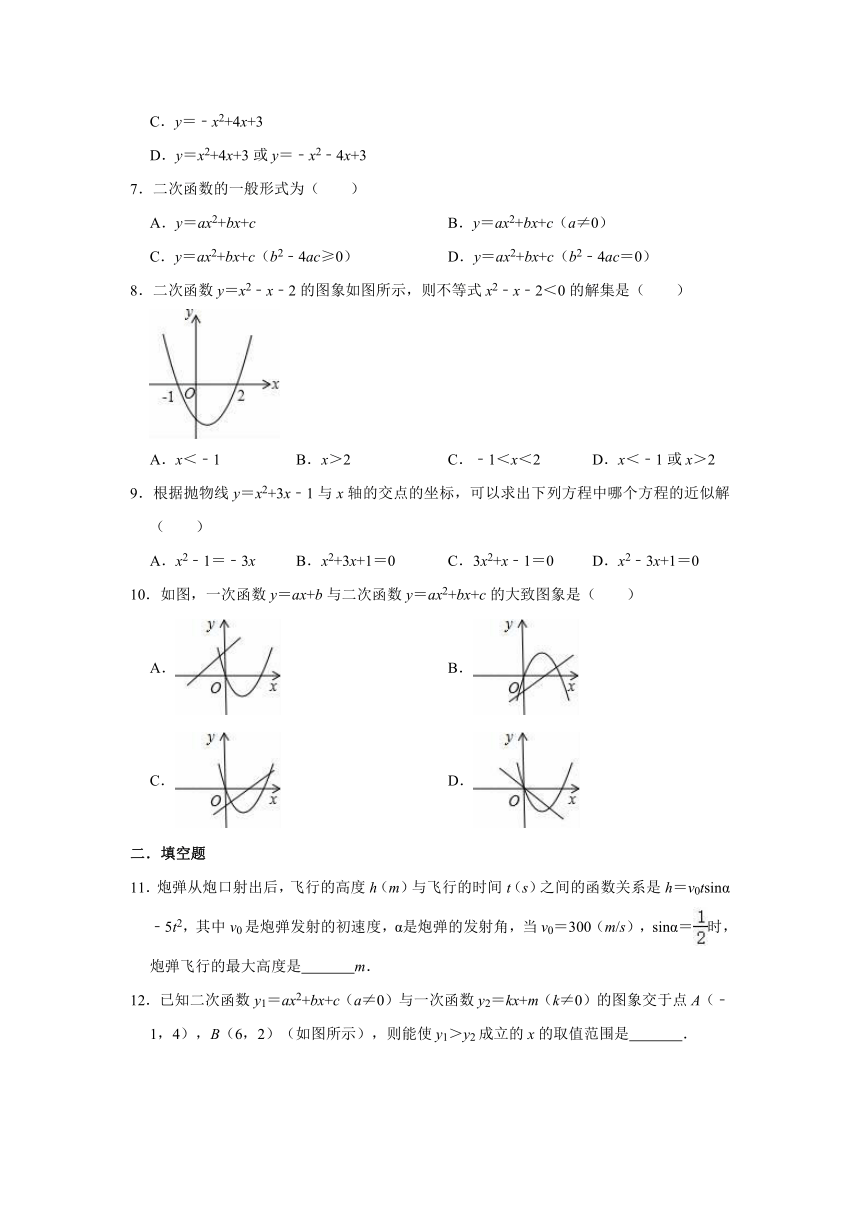
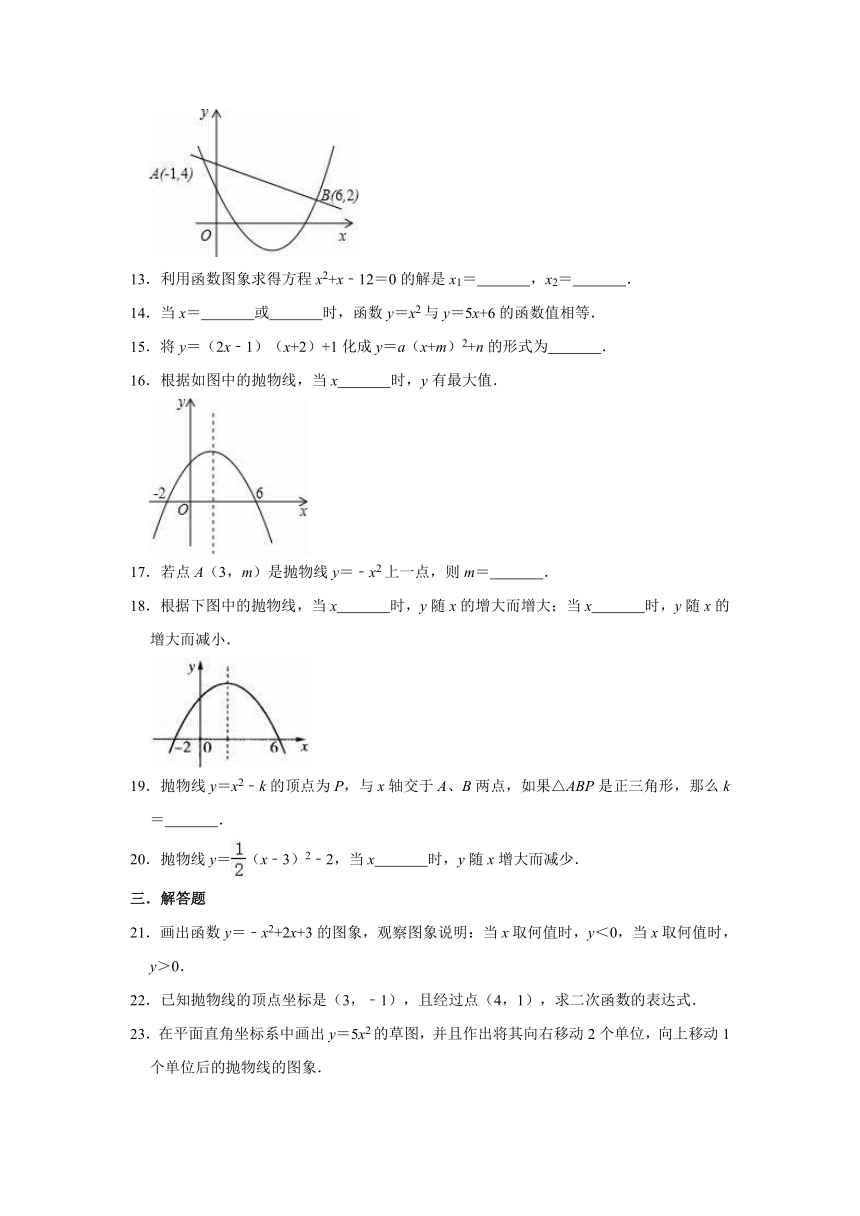


文档简介
2020-2021学年华东师大新版九年级下册数学《第26章
二次函数》单元测试卷
一.选择题
1.下列各式中,y是关于x的二次函数的是( )
A.x2y+x=1
B.x2﹣xy=5
C.y2=x2+2
D.x2+y+2=0
2.如图,已知二次函数y=x2+bx+c的图象的对称轴为过点(2,0)且与y轴平行的直线,点A、B均在图象上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3)
B.(3,2)
C.(3,3)
D.(4,3)
3.二次函数y=mx2+(6﹣2m)x+m﹣3的图象如图所示,则m的取值范围是( )
A.m>3
B.m<3
C.0≤m≤3
D.0<m<3
4.下列各点不在抛物线y=﹣x2+4x﹣1上的是( )
A.(﹣2,﹣13)
B.(﹣1,﹣4)
C.(﹣1,﹣6)
D.(2,3)
5.在平面直角坐标系中,抛物线关于x轴对称的抛物线的解析式为( )
A.
B.
C.
D.
6.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
7.二次函数的一般形式为( )
A.y=ax2+bx+c
B.y=ax2+bx+c(a≠0)
C.y=ax2+bx+c(b2﹣4ac≥0)
D.y=ax2+bx+c(b2﹣4ac=0)
8.二次函数y=x2﹣x﹣2的图象如图所示,则不等式x2﹣x﹣2<0的解集是( )
A.x<﹣1
B.x>2
C.﹣1<x<2
D.x<﹣1或x>2
9.根据抛物线y=x2+3x﹣1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A.x2﹣1=﹣3x
B.x2+3x+1=0
C.3x2+x﹣1=0
D.x2﹣3x+1=0
10.如图,一次函数y=ax+b与二次函数y=ax2+bx+c的大致图象是( )
A.
B.
C.
D.
二.填空题
11.炮弹从炮口射出后,飞行的高度h(m)与飞行的时间t(s)之间的函数关系是h=v0tsinα﹣5t2,其中v0是炮弹发射的初速度,α是炮弹的发射角,当v0=300(m/s),sinα=时,炮弹飞行的最大高度是
m.
12.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(﹣1,4),B(6,2)(如图所示),则能使y1>y2成立的x的取值范围是
.
13.利用函数图象求得方程x2+x﹣12=0的解是x1=
,x2=
.
14.当x=
或
时,函数y=x2与y=5x+6的函数值相等.
15.将y=(2x﹣1)(x+2)+1化成y=a(x+m)2+n的形式为
.
16.根据如图中的抛物线,当x
时,y有最大值.
17.若点A(3,m)是抛物线y=﹣x2上一点,则m=
.
18.根据下图中的抛物线,当x
时,y随x的增大而增大;当x
时,y随x的增大而减小.
19.抛物线y=x2﹣k的顶点为P,与x轴交于A、B两点,如果△ABP是正三角形,那么k=
.
20.抛物线y=(x﹣3)2﹣2,当x
时,y随x增大而减少.
三.解答题
21.画出函数y=﹣x2+2x+3的图象,观察图象说明:当x取何值时,y<0,当x取何值时,y>0.
22.已知抛物线的顶点坐标是(3,﹣1),且经过点(4,1),求二次函数的表达式.
23.在平面直角坐标系中画出y=5x2的草图,并且作出将其向右移动2个单位,向上移动1个单位后的抛物线的图象.
24.已知是x的二次函数,求出它的解析式.
25.已知抛物线y=x2+3x﹣1.变换式子,指出抛物线的开口方向、对称轴和顶点坐标.
26.如图甲所示,已知抛物线经过原点O和x轴上另一点E,顶点M的坐标为(2,4);
(1)求抛物线函数关系式;
(2)矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3,将矩形ABCD以每秒1个单位长度的速度从图甲所示的位置沿x轴的正方向匀速平移,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图乙所示).
①当时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
③现将甲图中的抛物线向右平移m(m>0)个单位,所得抛物线与x轴交于G、F两点,与原抛物线交于点Q,设△FGQ的面积为S,求S关于m的函数关系式.
27.已知二次函数y=x2+mx+m﹣5,
(1)求证:不论m取何值时,抛物线总与x轴有两个交点;
(2)求当m取何值时,抛物线与x轴两交点之间的距离最短.
参考答案与试题解析
一.选择题
1.解:A、整理后,不符合二次函数的一般形式,错误;
B、整理后,不符合二次函数的一般形式,错误;
C、这里,y的指数是2,不是函数,错误;
D、整理为y=﹣x2﹣2,是二次函数,正确.
故选:D.
2.解:∵二次函数y=x2+bx+c的图象的对称轴为过点(2,0)且与y轴平行的直线,
∴对称轴为x=2,
∵点A的坐标为(0,3),
∴点B的坐标为(4,3),
故选:D.
3.解:∵抛物线的开口向上,
∴m>0,①
∵对称轴在y轴的左侧,
∴x=﹣<0,②
∵二次函数与y轴交于负半轴,
∴m﹣3<0,③
∵抛物线与x轴有两个交点(b2﹣4ac>0),
∴(6﹣2m)2﹣4m(m﹣3)>0,④,
联立①②③④解之得:0<m<3.
∴m的取值范围是0<m<3.
故选:D.
4.解:A、把(﹣2,﹣13)中x=﹣2代入得y=﹣4﹣8﹣1=﹣13,不成立;
B、把(﹣1,﹣4)中x=﹣1代入得y=﹣1﹣4﹣1=﹣6≠﹣4,成立;
C、把(﹣1,﹣2)中x=﹣1代入得y=﹣1﹣4﹣1=﹣6,不成立;
D、把(2,3)中x=2代入得y=﹣4+8﹣1=3,不成立.
故选:B.
5.解:∵抛物线关于x轴对称的抛物线为﹣,
∴所求解析式为:y=﹣(x+)2+.
故选:D.
6.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
7.解:根据一元二次方程的一般形式的概念知,应为y=ax2+bx+c(a≠0,a、b、c为常数),
故选:B.
8.解:由图可知,抛物线与x轴的交点为(﹣1,0)、(2,0),
所以,不等式x2﹣x﹣2<0的解集是﹣1<x<2.
故选:C.
9.解:∵抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根,
∴可以求出方程x2+3x﹣1=0的根,
方程x2﹣1=﹣3x与方程x2+3x﹣1=0等价,
∴可以求出方程x2﹣1=﹣3x的根.
故选:A.
10.解:A、由一次函数y=kx+b的图象可得:a>0,b>0,此时二次函数y=ax2+bx+c的图象应该开口向上,对称轴x=﹣<0,错误;
B、由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+bx+c的图象应该开口向上,错误;
C、由一次函数y=ax+b的图象可得:a>0,b<0,此时二次函数y=ax2+bx+c的图象应该开口向上,对称轴x=﹣>0,正确.
D、由一次函数y=ax+b的图象可得:a<0,b<0,此时二次函数y=ax2+bx+c的图象应该开口向下,错误;
故选:C.
二.填空题
11.解;∵当v0=300(m/s),sinα=时
h=300×t﹣5t2,
=150t﹣5t2
∴炮弹飞行的最大高度是:
=1125m.
故答案为:1125.
12.解:∵两函数图象的交点坐标为A(﹣1,4),B(6,2),
∴使y1>y2成立的x的取值范围是x<﹣1或x>6.
故答案为:x<﹣1或x>6.
13.解:∵方程x2+x﹣12=0的解就是函数y=x2+x﹣12的图象与x轴的交点的横坐标,
而y=x2+x﹣12的图象如图所示:
∴y=x2+x﹣12的图象与x轴的交点坐标为(﹣4,0)、(3,0),
∴方程x2+x﹣12=0的解是x1=﹣4,x2=3.
14.解:由题意可知x2=5x+6
解得x=﹣1,x=6.
15.解:y=(2x﹣1)(x+2)+1,
=2x2+3x﹣1,
=2(x2+x+)﹣﹣1,
=2(x+)2﹣.
16.解:由图可得,对称轴为x==2,即当x=2时,y有最大值.
17.解:当x=3时,m=﹣32,即m=﹣9.
18.解:因为抛物线与x轴两交点坐标(﹣2,0),(6,0),
所以,抛物线对称轴为x==2,
所以,当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小.
19.解:∵抛物线y=x2﹣k的顶点为P,
∴P点的坐标为:(0,﹣k),∴PO=K,
∵抛物线y=x2﹣k与x轴交于A、B两点,且△ABP是正三角形,
∴OA=OB,∠OPB=30°,
∴tan30°==,
∴OB=k,
∴点B的坐标为:(
k,0),点B在抛物线y=x2﹣k上,
∴将B点代入y=x2﹣k,得:
0=(k)2﹣k,
整理得:﹣k=0,
解方程得:k1=0(不合题意舍去),k2=3.
故答案为:3.
20.解:∵抛物线y=(x﹣3)2﹣2的对称轴为:x=3,开口向上,
∴当x<3时,y随x增大而减少,
故答案为:x<3.
三.解答题
21.解:∵y=﹣x2+2x+3,
=﹣(x﹣1)2+4,
∴开口方向向下,对称轴x=1,顶点坐标(1,4),
令x=0得:y=3,
∴与y轴交点坐标(0,3),
令y=0得:﹣x2+2x+3=0,
∴x1=1
x2=3,
∴与x轴交点坐标(﹣1,0),(3,0),
作出函数如图所示的图象,
由图象可以看出:当x<﹣1或x>3时,y<0;
当﹣1<x<3时,y>0.
22.解:设抛物线解析式为y=a(x﹣3)2﹣1,
把(4,1)代入得a﹣1=1,解得a=2,
所以抛物线解析式为y=2(x﹣3)2﹣1.
23.解:原抛物线的顶点为(0,0),分别右移动2个单位,向上移动1个单位后,
那么新抛物线的顶点为(2,1);
可设新抛物线的解析式为y=5(x﹣h)2+k,代入得:
y=5(x﹣2)2+1.
24.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
25.解:y=x2+3x﹣1
=﹣(x2﹣6x)﹣1,
=﹣
[(x﹣3)2﹣9]﹣1,
=﹣
[(x﹣3)2+,
∴抛物线的开口方向向上、对称轴为x=3,顶点坐标为:(3,).
26.解:(1)设抛物线的解析式为:y=a(x﹣2)2+4,
∵抛物线过点m(2,4)和原点,
∴0=4a+4,
∴a=﹣1
∴抛物线的解析式为:y=﹣(x﹣2)2+4
(2)①∵y=﹣(x﹣2)2+4
∴当y=0时,﹣(x﹣2)2+4=0,
∴x1=0,x2=4,
∴E(4,0),
设直线ME的解析式为:y=kx+b,则
,
解得:,
∴直线ME的解析式为:y=﹣2x+8,
∵矩形ABCD以每秒1个单位长度的速度从图甲所示的位置沿x轴的正方向匀速平移,同时一动点P也以相同的速度从点A出发向B匀速移动,
∴当t=时,P(,)
∴当x=时,y=3≠,
∴当时,点P不在直线ME上.
②设点N(t,﹣(t﹣2)2+4),则P(t,t),
∴PN=﹣t2+3t,
∵AD=2,AB=3
∴S==﹣t2+3t+3,
∴S=﹣(t2﹣3t+﹣)+3=﹣(t﹣)2+
∴当t=时,S的最大值是;
③由题意可以知道经过F、G的抛物线的解析式为:y=﹣(x﹣2﹣m)2+4,
∵经过O、E的抛物线的解析式为:y=﹣(x﹣2)2+4,
∴,解得m=0(m>0,故舍去),或x=,
∴,
∴S==|﹣|
如图:当Q点在x轴的下方的时候,同样可以得出:
S==|﹣|
27.解:(1)根据b2﹣4ac与0的大小关系来判断二次函数与x轴交点的个数,
即m2﹣4×1×(m﹣5)=m2﹣4m+20=(m﹣2)2+16>0,
所以抛物线总与x轴有两个交点;
(2)设函数与x轴两个交点的值为x1,x2,且x2>x1,
x1+x2=﹣m,且x1?x2=m﹣5,
所以(x2﹣x1)2=(x1+x2)2﹣4x1x2=m2﹣4(m﹣5)=m2﹣4m+20=(m﹣2)2+16,
所以当m=2时,x2﹣x1有最小值4,
所以,抛物线与x轴两交点之间的距离最短为4.
二次函数》单元测试卷
一.选择题
1.下列各式中,y是关于x的二次函数的是( )
A.x2y+x=1
B.x2﹣xy=5
C.y2=x2+2
D.x2+y+2=0
2.如图,已知二次函数y=x2+bx+c的图象的对称轴为过点(2,0)且与y轴平行的直线,点A、B均在图象上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3)
B.(3,2)
C.(3,3)
D.(4,3)
3.二次函数y=mx2+(6﹣2m)x+m﹣3的图象如图所示,则m的取值范围是( )
A.m>3
B.m<3
C.0≤m≤3
D.0<m<3
4.下列各点不在抛物线y=﹣x2+4x﹣1上的是( )
A.(﹣2,﹣13)
B.(﹣1,﹣4)
C.(﹣1,﹣6)
D.(2,3)
5.在平面直角坐标系中,抛物线关于x轴对称的抛物线的解析式为( )
A.
B.
C.
D.
6.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
7.二次函数的一般形式为( )
A.y=ax2+bx+c
B.y=ax2+bx+c(a≠0)
C.y=ax2+bx+c(b2﹣4ac≥0)
D.y=ax2+bx+c(b2﹣4ac=0)
8.二次函数y=x2﹣x﹣2的图象如图所示,则不等式x2﹣x﹣2<0的解集是( )
A.x<﹣1
B.x>2
C.﹣1<x<2
D.x<﹣1或x>2
9.根据抛物线y=x2+3x﹣1与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A.x2﹣1=﹣3x
B.x2+3x+1=0
C.3x2+x﹣1=0
D.x2﹣3x+1=0
10.如图,一次函数y=ax+b与二次函数y=ax2+bx+c的大致图象是( )
A.
B.
C.
D.
二.填空题
11.炮弹从炮口射出后,飞行的高度h(m)与飞行的时间t(s)之间的函数关系是h=v0tsinα﹣5t2,其中v0是炮弹发射的初速度,α是炮弹的发射角,当v0=300(m/s),sinα=时,炮弹飞行的最大高度是
m.
12.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(﹣1,4),B(6,2)(如图所示),则能使y1>y2成立的x的取值范围是
.
13.利用函数图象求得方程x2+x﹣12=0的解是x1=
,x2=
.
14.当x=
或
时,函数y=x2与y=5x+6的函数值相等.
15.将y=(2x﹣1)(x+2)+1化成y=a(x+m)2+n的形式为
.
16.根据如图中的抛物线,当x
时,y有最大值.
17.若点A(3,m)是抛物线y=﹣x2上一点,则m=
.
18.根据下图中的抛物线,当x
时,y随x的增大而增大;当x
时,y随x的增大而减小.
19.抛物线y=x2﹣k的顶点为P,与x轴交于A、B两点,如果△ABP是正三角形,那么k=
.
20.抛物线y=(x﹣3)2﹣2,当x
时,y随x增大而减少.
三.解答题
21.画出函数y=﹣x2+2x+3的图象,观察图象说明:当x取何值时,y<0,当x取何值时,y>0.
22.已知抛物线的顶点坐标是(3,﹣1),且经过点(4,1),求二次函数的表达式.
23.在平面直角坐标系中画出y=5x2的草图,并且作出将其向右移动2个单位,向上移动1个单位后的抛物线的图象.
24.已知是x的二次函数,求出它的解析式.
25.已知抛物线y=x2+3x﹣1.变换式子,指出抛物线的开口方向、对称轴和顶点坐标.
26.如图甲所示,已知抛物线经过原点O和x轴上另一点E,顶点M的坐标为(2,4);
(1)求抛物线函数关系式;
(2)矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3,将矩形ABCD以每秒1个单位长度的速度从图甲所示的位置沿x轴的正方向匀速平移,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图乙所示).
①当时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
③现将甲图中的抛物线向右平移m(m>0)个单位,所得抛物线与x轴交于G、F两点,与原抛物线交于点Q,设△FGQ的面积为S,求S关于m的函数关系式.
27.已知二次函数y=x2+mx+m﹣5,
(1)求证:不论m取何值时,抛物线总与x轴有两个交点;
(2)求当m取何值时,抛物线与x轴两交点之间的距离最短.
参考答案与试题解析
一.选择题
1.解:A、整理后,不符合二次函数的一般形式,错误;
B、整理后,不符合二次函数的一般形式,错误;
C、这里,y的指数是2,不是函数,错误;
D、整理为y=﹣x2﹣2,是二次函数,正确.
故选:D.
2.解:∵二次函数y=x2+bx+c的图象的对称轴为过点(2,0)且与y轴平行的直线,
∴对称轴为x=2,
∵点A的坐标为(0,3),
∴点B的坐标为(4,3),
故选:D.
3.解:∵抛物线的开口向上,
∴m>0,①
∵对称轴在y轴的左侧,
∴x=﹣<0,②
∵二次函数与y轴交于负半轴,
∴m﹣3<0,③
∵抛物线与x轴有两个交点(b2﹣4ac>0),
∴(6﹣2m)2﹣4m(m﹣3)>0,④,
联立①②③④解之得:0<m<3.
∴m的取值范围是0<m<3.
故选:D.
4.解:A、把(﹣2,﹣13)中x=﹣2代入得y=﹣4﹣8﹣1=﹣13,不成立;
B、把(﹣1,﹣4)中x=﹣1代入得y=﹣1﹣4﹣1=﹣6≠﹣4,成立;
C、把(﹣1,﹣2)中x=﹣1代入得y=﹣1﹣4﹣1=﹣6,不成立;
D、把(2,3)中x=2代入得y=﹣4+8﹣1=3,不成立.
故选:B.
5.解:∵抛物线关于x轴对称的抛物线为﹣,
∴所求解析式为:y=﹣(x+)2+.
故选:D.
6.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
7.解:根据一元二次方程的一般形式的概念知,应为y=ax2+bx+c(a≠0,a、b、c为常数),
故选:B.
8.解:由图可知,抛物线与x轴的交点为(﹣1,0)、(2,0),
所以,不等式x2﹣x﹣2<0的解集是﹣1<x<2.
故选:C.
9.解:∵抛物线y=x2+3x﹣1与x轴的交点的横坐标就是方程x2+3x﹣1=0的根,
∴可以求出方程x2+3x﹣1=0的根,
方程x2﹣1=﹣3x与方程x2+3x﹣1=0等价,
∴可以求出方程x2﹣1=﹣3x的根.
故选:A.
10.解:A、由一次函数y=kx+b的图象可得:a>0,b>0,此时二次函数y=ax2+bx+c的图象应该开口向上,对称轴x=﹣<0,错误;
B、由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+bx+c的图象应该开口向上,错误;
C、由一次函数y=ax+b的图象可得:a>0,b<0,此时二次函数y=ax2+bx+c的图象应该开口向上,对称轴x=﹣>0,正确.
D、由一次函数y=ax+b的图象可得:a<0,b<0,此时二次函数y=ax2+bx+c的图象应该开口向下,错误;
故选:C.
二.填空题
11.解;∵当v0=300(m/s),sinα=时
h=300×t﹣5t2,
=150t﹣5t2
∴炮弹飞行的最大高度是:
=1125m.
故答案为:1125.
12.解:∵两函数图象的交点坐标为A(﹣1,4),B(6,2),
∴使y1>y2成立的x的取值范围是x<﹣1或x>6.
故答案为:x<﹣1或x>6.
13.解:∵方程x2+x﹣12=0的解就是函数y=x2+x﹣12的图象与x轴的交点的横坐标,
而y=x2+x﹣12的图象如图所示:
∴y=x2+x﹣12的图象与x轴的交点坐标为(﹣4,0)、(3,0),
∴方程x2+x﹣12=0的解是x1=﹣4,x2=3.
14.解:由题意可知x2=5x+6
解得x=﹣1,x=6.
15.解:y=(2x﹣1)(x+2)+1,
=2x2+3x﹣1,
=2(x2+x+)﹣﹣1,
=2(x+)2﹣.
16.解:由图可得,对称轴为x==2,即当x=2时,y有最大值.
17.解:当x=3时,m=﹣32,即m=﹣9.
18.解:因为抛物线与x轴两交点坐标(﹣2,0),(6,0),
所以,抛物线对称轴为x==2,
所以,当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小.
19.解:∵抛物线y=x2﹣k的顶点为P,
∴P点的坐标为:(0,﹣k),∴PO=K,
∵抛物线y=x2﹣k与x轴交于A、B两点,且△ABP是正三角形,
∴OA=OB,∠OPB=30°,
∴tan30°==,
∴OB=k,
∴点B的坐标为:(
k,0),点B在抛物线y=x2﹣k上,
∴将B点代入y=x2﹣k,得:
0=(k)2﹣k,
整理得:﹣k=0,
解方程得:k1=0(不合题意舍去),k2=3.
故答案为:3.
20.解:∵抛物线y=(x﹣3)2﹣2的对称轴为:x=3,开口向上,
∴当x<3时,y随x增大而减少,
故答案为:x<3.
三.解答题
21.解:∵y=﹣x2+2x+3,
=﹣(x﹣1)2+4,
∴开口方向向下,对称轴x=1,顶点坐标(1,4),
令x=0得:y=3,
∴与y轴交点坐标(0,3),
令y=0得:﹣x2+2x+3=0,
∴x1=1
x2=3,
∴与x轴交点坐标(﹣1,0),(3,0),
作出函数如图所示的图象,
由图象可以看出:当x<﹣1或x>3时,y<0;
当﹣1<x<3时,y>0.
22.解:设抛物线解析式为y=a(x﹣3)2﹣1,
把(4,1)代入得a﹣1=1,解得a=2,
所以抛物线解析式为y=2(x﹣3)2﹣1.
23.解:原抛物线的顶点为(0,0),分别右移动2个单位,向上移动1个单位后,
那么新抛物线的顶点为(2,1);
可设新抛物线的解析式为y=5(x﹣h)2+k,代入得:
y=5(x﹣2)2+1.
24.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
25.解:y=x2+3x﹣1
=﹣(x2﹣6x)﹣1,
=﹣
[(x﹣3)2﹣9]﹣1,
=﹣
[(x﹣3)2+,
∴抛物线的开口方向向上、对称轴为x=3,顶点坐标为:(3,).
26.解:(1)设抛物线的解析式为:y=a(x﹣2)2+4,
∵抛物线过点m(2,4)和原点,
∴0=4a+4,
∴a=﹣1
∴抛物线的解析式为:y=﹣(x﹣2)2+4
(2)①∵y=﹣(x﹣2)2+4
∴当y=0时,﹣(x﹣2)2+4=0,
∴x1=0,x2=4,
∴E(4,0),
设直线ME的解析式为:y=kx+b,则
,
解得:,
∴直线ME的解析式为:y=﹣2x+8,
∵矩形ABCD以每秒1个单位长度的速度从图甲所示的位置沿x轴的正方向匀速平移,同时一动点P也以相同的速度从点A出发向B匀速移动,
∴当t=时,P(,)
∴当x=时,y=3≠,
∴当时,点P不在直线ME上.
②设点N(t,﹣(t﹣2)2+4),则P(t,t),
∴PN=﹣t2+3t,
∵AD=2,AB=3
∴S==﹣t2+3t+3,
∴S=﹣(t2﹣3t+﹣)+3=﹣(t﹣)2+
∴当t=时,S的最大值是;
③由题意可以知道经过F、G的抛物线的解析式为:y=﹣(x﹣2﹣m)2+4,
∵经过O、E的抛物线的解析式为:y=﹣(x﹣2)2+4,
∴,解得m=0(m>0,故舍去),或x=,
∴,
∴S==|﹣|
如图:当Q点在x轴的下方的时候,同样可以得出:
S==|﹣|
27.解:(1)根据b2﹣4ac与0的大小关系来判断二次函数与x轴交点的个数,
即m2﹣4×1×(m﹣5)=m2﹣4m+20=(m﹣2)2+16>0,
所以抛物线总与x轴有两个交点;
(2)设函数与x轴两个交点的值为x1,x2,且x2>x1,
x1+x2=﹣m,且x1?x2=m﹣5,
所以(x2﹣x1)2=(x1+x2)2﹣4x1x2=m2﹣4(m﹣5)=m2﹣4m+20=(m﹣2)2+16,
所以当m=2时,x2﹣x1有最小值4,
所以,抛物线与x轴两交点之间的距离最短为4.
