28.1.2弧,弦,圆心角
图片预览







文档简介
(共40张PPT)
1、圆是对称图形吗?它有哪些对称性?
回顾:
圆既是轴对称图形,又是中心对称图
形,也是旋转对称图形。旋转角度可以是任
意度数。对称轴是过圆心任意一条直线。
2、能否用手中的圆演示出它的各种对称性呢?圆的对称轴在哪里,对称中心和旋转中心在哪里?
复习
1、圆的对称性有哪几方面?
O
轴对称性
导入
2、将圆绕圆心任意旋转:
O
α
圆具有旋转不变性,是中心对称图形
.
O
B
A
180°
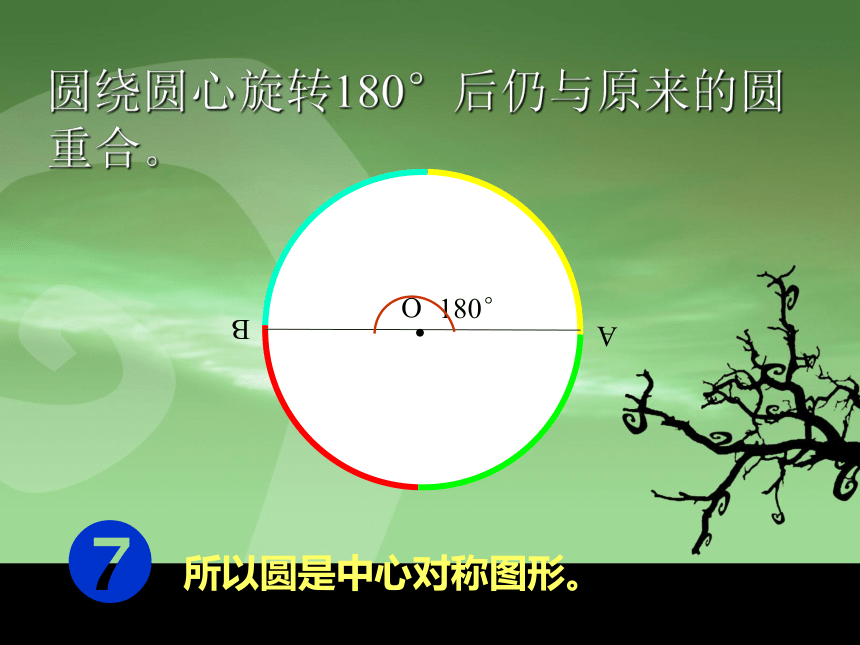
所以圆是中心对称图形。
圆绕圆心旋转180°后仍与原来的圆重合。
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
二、概念
如图中所示, ∠AOB就是一个圆心角。
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为M,
O
A
B
M
有关概念: 顶点在圆心的角,叫圆心角,
如 ,
所对的弦为AB;
则垂线段OM的长度,即圆心到弦的距离,叫弦心距 ,
如图,OM为AB弦的弦心距。
任意给圆心角,对应出现四个量:
圆心角
弧
弦 弦心距
探究
O
α
A
B
A′
B ′
α
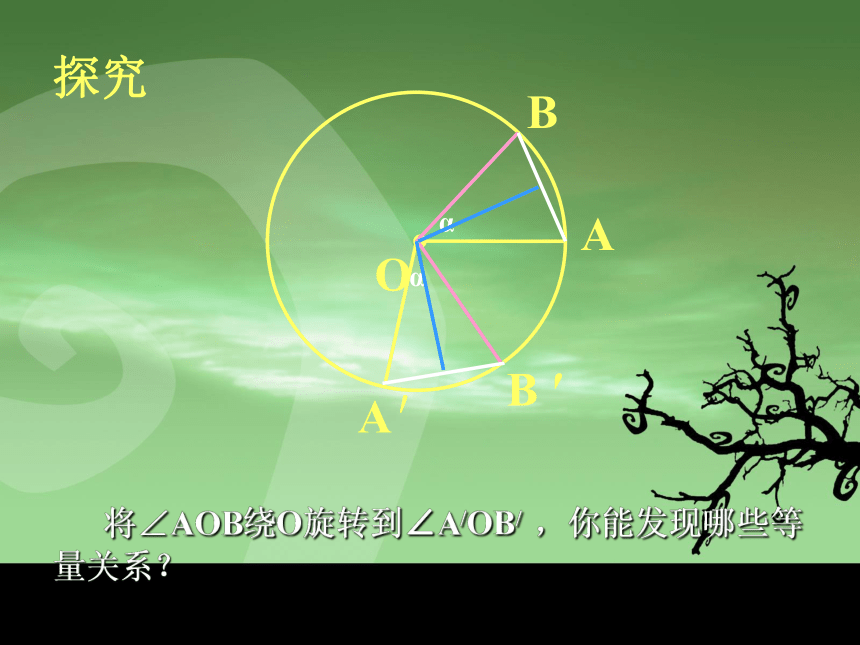
将∠AOB绕O旋转到∠A/OB/ ,你能发现哪些等量关系?
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB=∠A′OB′,射线OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合.
·
O
A
B
·
O
A
B
A′
B′
A′
B′
三、探究
因此,弧AB与弧A1B1 重合,AB与A′B′重合.
⌒
AB
⌒
A1B1
=
相等
(或等圆)
相等
相等
相等
3.在同一个圆 中,如果弦相等,那么所对的圆心角_____、所对的弧______,所对的弦的弦心距_____。
2.在同一个圆 中,如果弧相等,那么所对的圆心角_____、所对的弦______, 所对的弦的弦心距_____。
1.在同一个圆 中,如果圆心角相等,那么它所对的弧相等、所对的弦相等, 所对的弦的弦心距也相等。
结论:
相等
以上三句话如没有在同圆或等圆中,这个结论还会成立吗?
(或等圆)
(或等圆)
相等
新授
O
α
A
B
A′
B ′
α
在同圆或等圆中,相等的圆心角所对
的弧相等,所对的弦相等,所对的弦
的弦心距相等。
等对等定理
(1) 圆心角
(2) 弧
(3) 弦
(4) 弦心距
延伸
O
α
A
B
A′
B ′
α
(1) 圆心角
(2) 弧
(3) 弦
(4) 弦心距
等对等定理整体理解:
知一得三
1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 = ,那么____________,______________.
(3)如果∠AOB=∠COD,那么_____________,____________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
相 等
因为AB=CD ,所以∠AOB=∠COD.
又因为AO=CO,BO=DO,
所以△AOB ≌ △COD.
又因为OE 、OF是AB与CD对应边上的高,
所以 OE = OF.
练习
⌒
CD
⌒
AB
⌒
AB
⌒
CD
=
⌒
AB
⌒
CD
=
二.判断下列说法是否正确:
1相等的圆心角所对的弧相等。( )
2相等的弧所对的弦相等。( )
3相等的弦所对的弧相等。( )
三.如图,⊙O中,AB=CD,
,则
O
D
C
A
B
1
2
试一试你的能力
×
√
50
o
×
1.如图,在⊙O中,AB=AC,∠B=70°.
求∠C度数.
2.如图,AB是直径,BC=CD=DE,
∠BOC=40°,求∠AOE的度数
︵
︵
︵
︵
︵
.3如图,已知AD=BC,
试说明AB=CD
︵
︵
点悟:
在同圆或等圆中,如果两条弧相等,那么它们所对的
圆心角相等,所对的弦相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的
圆心角相等,所对的弧相等。
如图,在⊙O中,AC=BD,
,求∠2的度数。
你会做吗?
解:
∵
AC=BD
(已知)
∴
∴
AB=CD
∴
AC-BC=BD-BC
(等式的性质)
∠1=∠2=45°
(在同圆中,相等的弧所对的圆心角相等)
例3:已知:如图, AB、DE是⊙O的两条直径,C是⊙O上一点,且AD=CE。求证:BE=CE
⌒
⌒
O
C
B
A
D
E
O
C
B
A
例4:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。
(1)∠AOB、∠COB、∠AOC的度数分别为__________
(2)若⊙O的半径为r,则等边ABC三角形的边长为_______
O
C
B
A
D
P
例4:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。
(3)延长AO,分别交BC于点P,BC于点D,连结BD,CD。试判断四边形BDCO是哪一种特殊四边形,并说明理由。
⌒
1°弧
n°
1°
n°弧
∵把圆心角等分成360份,则每一份的圆心角是1 .同时整个圆也被分成了360份.
则每一份这样的弧叫做1 的弧.
这样,1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
小结
(2) 所对的圆心角和 所对的圆 心角相等
在两个圆中,分别有 , 若 的度数和 相等,则有
(1) 和 相等
判断
1.在半径相等的⊙O和⊙O 中,AB和A B 所对的圆心
角都是60°.
(1)AB和A B各是多少度
(2)AB和A B 相等吗
(3)在同圆或等圆中,度数相度的弧相等.为什么
2.若把圆5等分,那么每一份弧是多少度 若把圆8等分,那么
每一份弧是多少度
3.圆心到弦的距离叫做这条弦的弦心距.求证:在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.
⌒
⌒
⌒
⌒
⌒
⌒
结束
试一试
探究二:
动手操作:
如何将圆两等分?四等分?八等分?
你还可以将圆多少等分呢?
总结
1.圆是旋转对称图形、中心对称图形,它的对称中心是圆心;
2.圆心角、弧、弦之间的关系。
注意:
(1)运用此性质的前提是:在同圆或等圆中.
(2)由一个条件,可以得到多个结论.
(3)本知识是证明弦相等、弧相等的常用方法.
圆的基本性质
1.弧、弦、弦心距与圆心角之间的关系:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两弦的弦心距中,有一组量相等,那么它们所对应的其余各组量也分别相等.
1、圆是对称图形吗?它有哪些对称性?
回顾:
圆既是轴对称图形,又是中心对称图
形,也是旋转对称图形。旋转角度可以是任
意度数。对称轴是过圆心任意一条直线。
2、能否用手中的圆演示出它的各种对称性呢?圆的对称轴在哪里,对称中心和旋转中心在哪里?
复习
1、圆的对称性有哪几方面?
O
轴对称性
导入
2、将圆绕圆心任意旋转:
O
α
圆具有旋转不变性,是中心对称图形
.
O
B
A
180°
所以圆是中心对称图形。
圆绕圆心旋转180°后仍与原来的圆重合。
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
二、概念
如图中所示, ∠AOB就是一个圆心角。
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为M,
O
A
B
M
有关概念: 顶点在圆心的角,叫圆心角,
如 ,
所对的弦为AB;
则垂线段OM的长度,即圆心到弦的距离,叫弦心距 ,
如图,OM为AB弦的弦心距。
任意给圆心角,对应出现四个量:
圆心角
弧
弦 弦心距
探究
O
α
A
B
A′
B ′
α
将∠AOB绕O旋转到∠A/OB/ ,你能发现哪些等量关系?
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB=∠A′OB′,射线OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合.
·
O
A
B
·
O
A
B
A′
B′
A′
B′
三、探究
因此,弧AB与弧A1B1 重合,AB与A′B′重合.
⌒
AB
⌒
A1B1
=
相等
(或等圆)
相等
相等
相等
3.在同一个圆 中,如果弦相等,那么所对的圆心角_____、所对的弧______,所对的弦的弦心距_____。
2.在同一个圆 中,如果弧相等,那么所对的圆心角_____、所对的弦______, 所对的弦的弦心距_____。
1.在同一个圆 中,如果圆心角相等,那么它所对的弧相等、所对的弦相等, 所对的弦的弦心距也相等。
结论:
相等
以上三句话如没有在同圆或等圆中,这个结论还会成立吗?
(或等圆)
(或等圆)
相等
新授
O
α
A
B
A′
B ′
α
在同圆或等圆中,相等的圆心角所对
的弧相等,所对的弦相等,所对的弦
的弦心距相等。
等对等定理
(1) 圆心角
(2) 弧
(3) 弦
(4) 弦心距
延伸
O
α
A
B
A′
B ′
α
(1) 圆心角
(2) 弧
(3) 弦
(4) 弦心距
等对等定理整体理解:
知一得三
1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 = ,那么____________,______________.
(3)如果∠AOB=∠COD,那么_____________,____________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
相 等
因为AB=CD ,所以∠AOB=∠COD.
又因为AO=CO,BO=DO,
所以△AOB ≌ △COD.
又因为OE 、OF是AB与CD对应边上的高,
所以 OE = OF.
练习
⌒
CD
⌒
AB
⌒
AB
⌒
CD
=
⌒
AB
⌒
CD
=
二.判断下列说法是否正确:
1相等的圆心角所对的弧相等。( )
2相等的弧所对的弦相等。( )
3相等的弦所对的弧相等。( )
三.如图,⊙O中,AB=CD,
,则
O
D
C
A
B
1
2
试一试你的能力
×
√
50
o
×
1.如图,在⊙O中,AB=AC,∠B=70°.
求∠C度数.
2.如图,AB是直径,BC=CD=DE,
∠BOC=40°,求∠AOE的度数
︵
︵
︵
︵
︵
.3如图,已知AD=BC,
试说明AB=CD
︵
︵
点悟:
在同圆或等圆中,如果两条弧相等,那么它们所对的
圆心角相等,所对的弦相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的
圆心角相等,所对的弧相等。
如图,在⊙O中,AC=BD,
,求∠2的度数。
你会做吗?
解:
∵
AC=BD
(已知)
∴
∴
AB=CD
∴
AC-BC=BD-BC
(等式的性质)
∠1=∠2=45°
(在同圆中,相等的弧所对的圆心角相等)
例3:已知:如图, AB、DE是⊙O的两条直径,C是⊙O上一点,且AD=CE。求证:BE=CE
⌒
⌒
O
C
B
A
D
E
O
C
B
A
例4:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。
(1)∠AOB、∠COB、∠AOC的度数分别为__________
(2)若⊙O的半径为r,则等边ABC三角形的边长为_______
O
C
B
A
D
P
例4:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC。
(3)延长AO,分别交BC于点P,BC于点D,连结BD,CD。试判断四边形BDCO是哪一种特殊四边形,并说明理由。
⌒
1°弧
n°
1°
n°弧
∵把圆心角等分成360份,则每一份的圆心角是1 .同时整个圆也被分成了360份.
则每一份这样的弧叫做1 的弧.
这样,1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
小结
(2) 所对的圆心角和 所对的圆 心角相等
在两个圆中,分别有 , 若 的度数和 相等,则有
(1) 和 相等
判断
1.在半径相等的⊙O和⊙O 中,AB和A B 所对的圆心
角都是60°.
(1)AB和A B各是多少度
(2)AB和A B 相等吗
(3)在同圆或等圆中,度数相度的弧相等.为什么
2.若把圆5等分,那么每一份弧是多少度 若把圆8等分,那么
每一份弧是多少度
3.圆心到弦的距离叫做这条弦的弦心距.求证:在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.
⌒
⌒
⌒
⌒
⌒
⌒
结束
试一试
探究二:
动手操作:
如何将圆两等分?四等分?八等分?
你还可以将圆多少等分呢?
总结
1.圆是旋转对称图形、中心对称图形,它的对称中心是圆心;
2.圆心角、弧、弦之间的关系。
注意:
(1)运用此性质的前提是:在同圆或等圆中.
(2)由一个条件,可以得到多个结论.
(3)本知识是证明弦相等、弧相等的常用方法.
圆的基本性质
1.弧、弦、弦心距与圆心角之间的关系:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两弦的弦心距中,有一组量相等,那么它们所对应的其余各组量也分别相等.
