28.2.1点与圆的位置关系课件
图片预览



文档简介
(共17张PPT)
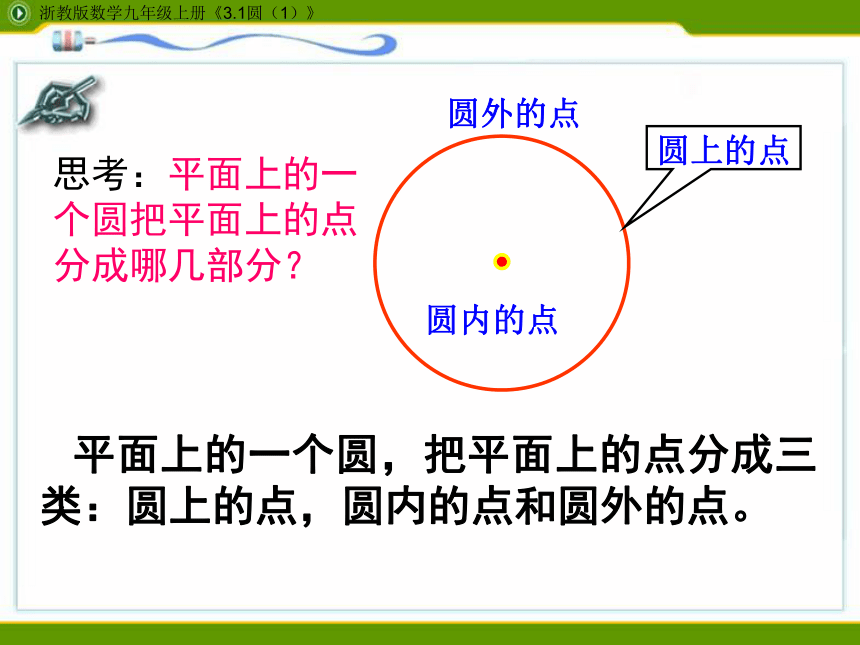
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。
思考:平面上的一个圆把平面上的点分成哪几部分?
28.2.3
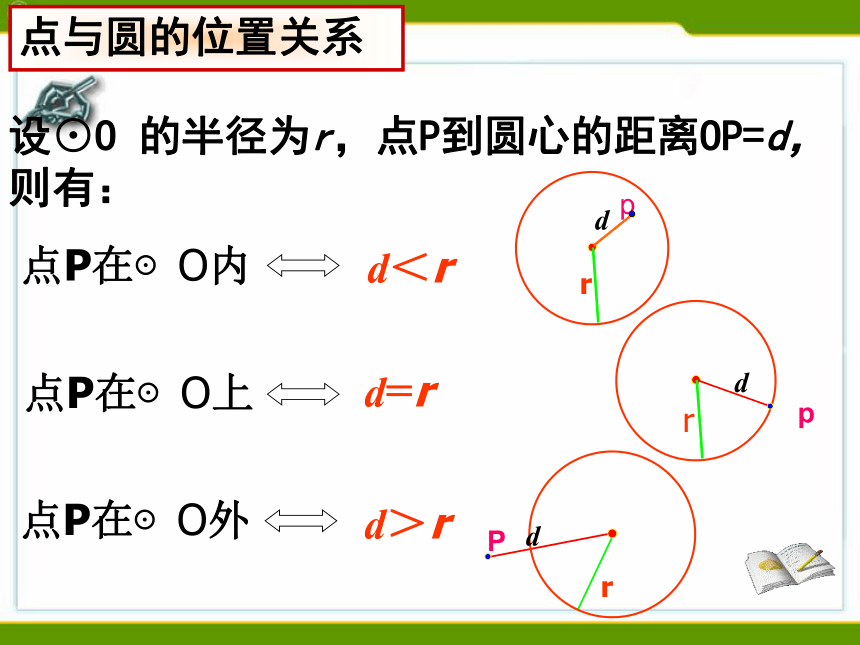
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d<r
d=r
d>r
r
p
d
p
r
d
P
r
d
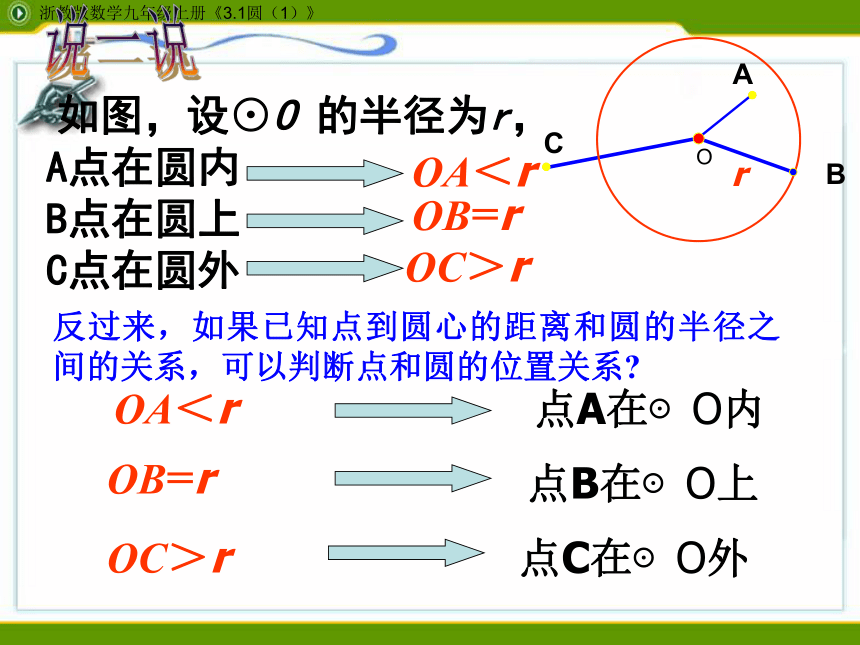
如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
C点在圆外
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系
OA<r
OB=r
OC>r
A
B
C
r
OA<r
OB=r
OC>r
O
已知⊙O的面积为25π。
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
(4)若点P不在圆外,则PO 。
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
2、⊙O的半径6cm,当OP=6时,点A在 ;
当OP ( ) 时点P在圆内;当OP 时,点P不在圆外。
3、正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。
4、已知AB为⊙O的直径P为⊙O 上任意一点,则点关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
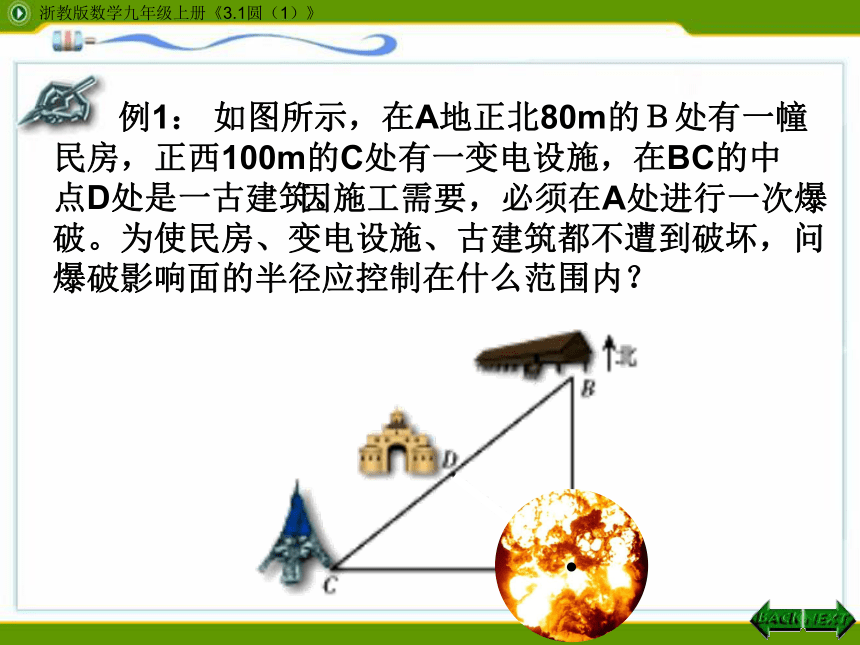
例1: 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。
因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
在直角三角形ABC中,∠C=Rt∠,AC=3cm,AB=5cm。若以点C为圆心,画一个半径为3cm的圆,试判断点A,点B和AB的中点D与⊙C的位置关系。
C
A
B
例2:在平面直角坐标系中,⊙P的圆心P(1,2),⊙P的半径为r。
①若r=2,试判断原点与⊙P的位置关系?
②当r满足什么条件时,原点在⊙P外?
例3、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?
练 习
3、一个点到已知圆上的点的最大距离是8,最小距离是2,则圆的半径是____
2、如图,⊿ABC中,∠C=90°,
BC=3,AC=6,CD为中线,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
1、已知圆P的半径为3,点Q在圆P外,点R在圆P上,点H在圆P内,则PQ___3,PR____3,PH_____3.
如图,一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
用一用
5
三、巩固新知 应用新知
若改为5m呢?
改为6m呢?
5m
o
4m
5m
o
4m
正确答案
课堂练习:
2已知⊙O的半径是5cm,A为线段OP的中点,
当OP满足下列条件时,分别指出点A与⊙O的位置关系:
当OP= 6cm时, ;
当OP=10cm时, ;
当OP=14cm时, 。
1、正方形ABCD的边长为3cm,以A为圆心,3cm长为半径作⊙A,则点A在⊙A ,点B在⊙A ,点C在⊙A ,点D在⊙A 。
想一想
一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个 怎样安装 请说明理由.
8
10
6
A
B
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。
思考:平面上的一个圆把平面上的点分成哪几部分?
28.2.3
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d<r
d=r
d>r
r
p
d
p
r
d
P
r
d
如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
C点在圆外
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系
OA<r
OB=r
OC>r
A
B
C
r
OA<r
OB=r
OC>r
O
已知⊙O的面积为25π。
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
(4)若点P不在圆外,则PO 。
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
2、⊙O的半径6cm,当OP=6时,点A在 ;
当OP ( ) 时点P在圆内;当OP 时,点P不在圆外。
3、正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A ;点C在⊙A ;点D在⊙A 。
4、已知AB为⊙O的直径P为⊙O 上任意一点,则点关于AB的对称点P′与⊙O的位置为( )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
例1: 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。
因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
在直角三角形ABC中,∠C=Rt∠,AC=3cm,AB=5cm。若以点C为圆心,画一个半径为3cm的圆,试判断点A,点B和AB的中点D与⊙C的位置关系。
C
A
B
例2:在平面直角坐标系中,⊙P的圆心P(1,2),⊙P的半径为r。
①若r=2,试判断原点与⊙P的位置关系?
②当r满足什么条件时,原点在⊙P外?
例3、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?
练 习
3、一个点到已知圆上的点的最大距离是8,最小距离是2,则圆的半径是____
2、如图,⊿ABC中,∠C=90°,
BC=3,AC=6,CD为中线,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
1、已知圆P的半径为3,点Q在圆P外,点R在圆P上,点H在圆P内,则PQ___3,PR____3,PH_____3.
如图,一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
用一用
5
三、巩固新知 应用新知
若改为5m呢?
改为6m呢?
5m
o
4m
5m
o
4m
正确答案
课堂练习:
2已知⊙O的半径是5cm,A为线段OP的中点,
当OP满足下列条件时,分别指出点A与⊙O的位置关系:
当OP= 6cm时, ;
当OP=10cm时, ;
当OP=14cm时, 。
1、正方形ABCD的边长为3cm,以A为圆心,3cm长为半径作⊙A,则点A在⊙A ,点B在⊙A ,点C在⊙A ,点D在⊙A 。
想一想
一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个 怎样安装 请说明理由.
8
10
6
A
B
