切线的复习
图片预览



文档简介
(共16张PPT)
(复习课)
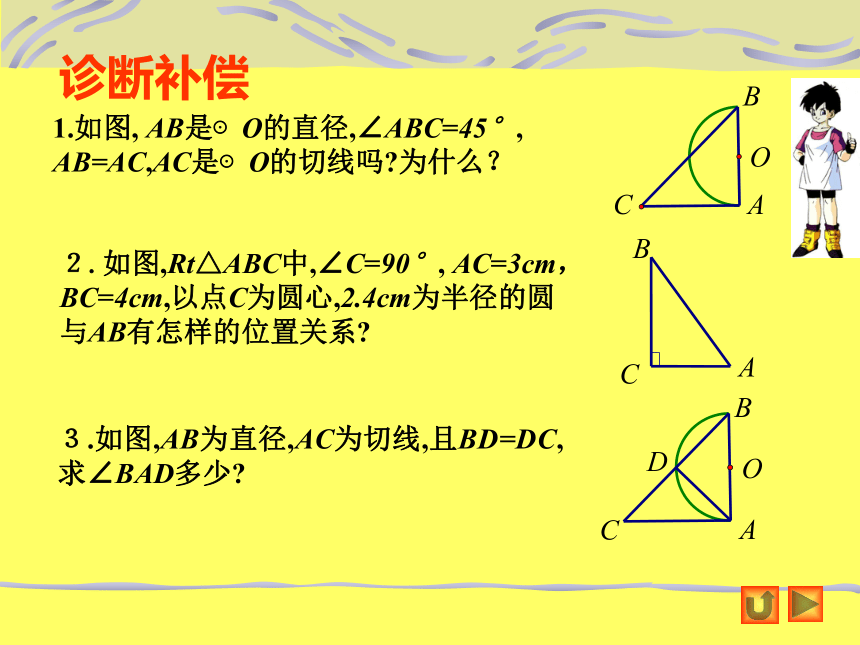
诊断补偿
1.如图, AB是⊙O的直径,∠ABC=45°,
AB=AC,AC是⊙O的切线吗 为什么?
3.如图,AB为直径,AC为切线,且BD=DC,求∠BAD多少
2.如图,Rt△ABC中,∠C=90°, AC=3cm,BC=4cm,以点C为圆心,2.4cm为半径的圆与AB有怎样的位置关系
B
C
O
A
B
A
C
B
D
C
O
A
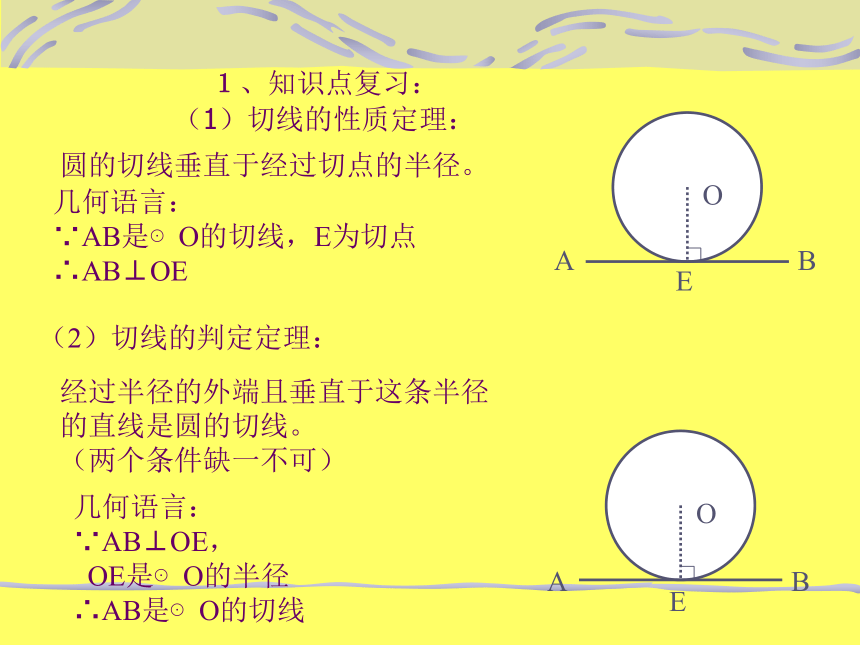
1、知识点复习:
(1)切线的性质定理:
(2)切线的判定定理:
A
O
B
E
A
O
B
E
几何语言: ∵AB是⊙O的切线,E为切点 ∴AB⊥OE
圆的切线垂直于经过切点的半径。
几何语言:
∵AB⊥OE,
OE是⊙O的半径
∴AB是⊙O的切线
经过半径的外端且垂直于这条半径的直线是圆的切线。
(两个条件缺一不可)
圆的切线垂直于过切点的直径
经过直径的一端并且垂直于直径的直线是圆的切线.
直线L与圆相切
d = r
切线的性质
切线的判定
范例提炼
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点切线互相垂直,垂足为D. 求证:AC平分∠DAB
连结OC
∵CD是⊙O的切线∴OC⊥CD
又∵CD⊥AD∴OC∥AD ∴∠1=∠3
又∵OA=OC
∴∠2=∠3 ∴ ∠1=∠2
即AC平分∠DAB
证明:
小提示:连结圆心与切点是作辅助线常用的方法之一.
3
2
1
O
B
A
C
D
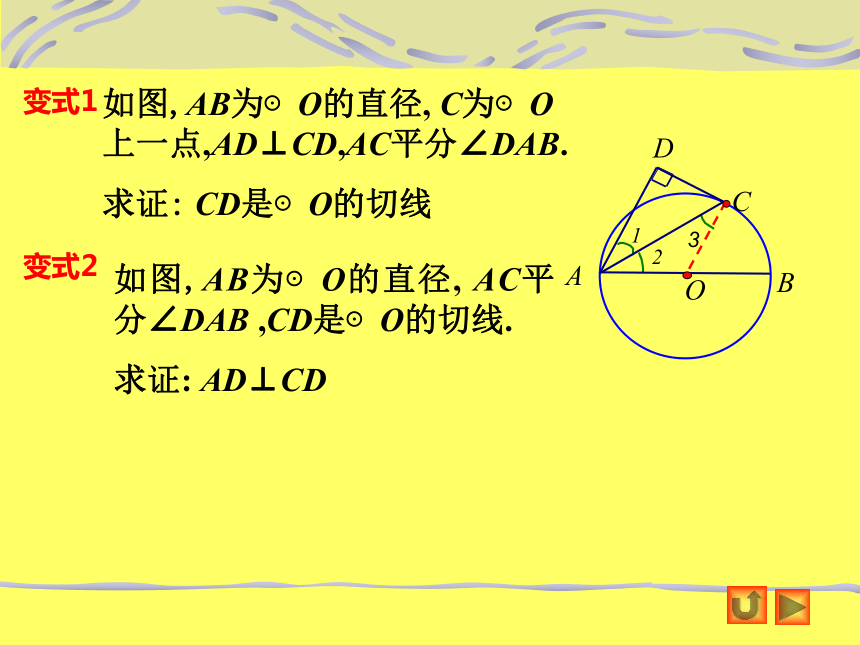
如图,AB为⊙O的直径, C为⊙O上一点,AD⊥CD,AC平分∠DAB.
求证: CD是⊙O的切线
变式1
变式2
如图,AB为⊙O的直径, AC平分∠DAB ,CD是⊙O的切线.
求证: AD⊥CD
3
2
1
B
O
A
C
D
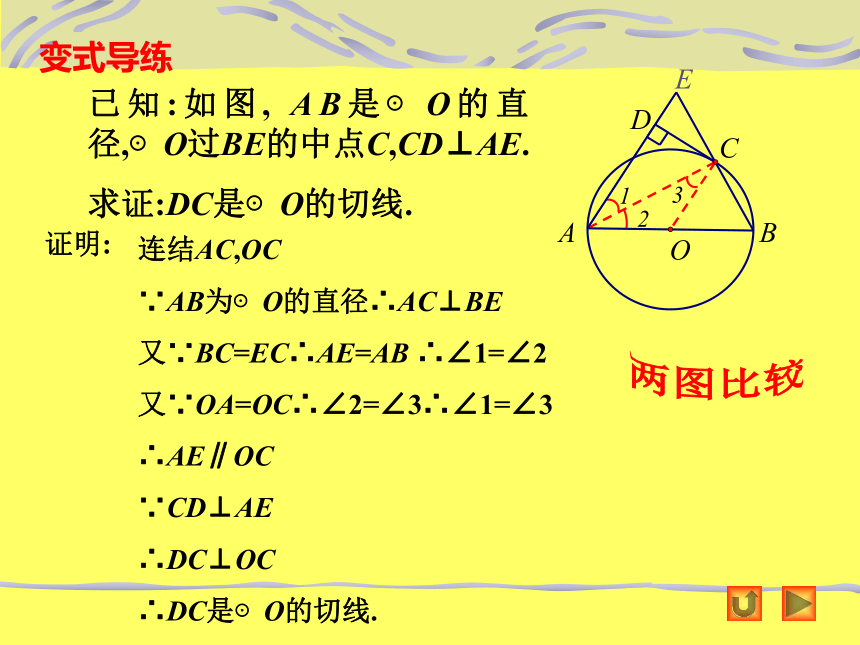
变式导练
已知:如图, AB是⊙O的直径,⊙O过BE的中点C,CD⊥AE.
求证:DC是⊙O的切线.
证明:
连结AC,OC
∵AB为⊙O的直径∴AC⊥BE
又∵BC=EC∴AE=AB ∴∠1=∠2
又∵OA=OC∴∠2=∠3∴∠1=∠3
∴AE∥OC
∵CD⊥AE
∴DC⊥OC
∴DC是⊙O的切线.
3
2
1
B
O
A
C
D
E
B
O
A
C
D
B
O
A
C
D
E
能力提高
已知:AB是⊙O的直径, ⊙O过AC的中点,DE⊥BC,垂足为E.
⑴这些条件你能推出哪些正确的结论 (所连辅助线不要出现在结论中.不写推理过程,写出3个结论即可)
⑵当∠ABC为直角时,其他条件不变,除上述结论外,你还能推出哪些正确的结论 (要求将图画出,写出4个结论取即可)
E
D
C
O
B
A
如图,在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的圆O交AB于点E,⊙O切线EF交BC于点F
求证:EF⊥BC
A
E
B
D
C
F
O
(变式:作半径证垂直)
已知在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的圆O交AB于点E,EF⊥BC
求证:EF是⊙O的切线
证明:连结OE
∵梯形ABCD中,AB∥CD,AD=BC
∴∠A=∠B
∵OA=OE
∴∠A=∠OEA
∴∠OEA=∠B
∴OE∥BC
∵EF⊥BC
∴EF⊥OE
又OE是⊙O的半径
∴EF是⊙O的切线
9年衡阳市)如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60 .
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从A点出发沿着AB
方向运动,同时动点F以1cm/s的速度从B点出发
沿BC方向运动,设运动时间为t秒(0连结EF,当 为何值时,△BEF为直角三角形.
交流评价
本节课你的收获是什么
切线的性质
圆的切线垂直于过切点的直径
切线的判定
经过直径的一端并且垂直于直径的直线是圆的切线.
直线L与圆相切
d = r
一种常用的辅助线
连结圆心与切点是作辅助线常用的方法之一.
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑴试猜想PC与⊙D的位置关系,并说明理由.
分析:做此类题,尤其强调
数形结合,同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证?联
想证明切线的两种方法。点
C在圆上,即证:∠DCP=90°
利用勾股及逆定理可得。
切
线
判
定
令x=0,得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5
又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20
在△CPD中, CD2+CP2=5+20=25, DP2=25
∴CD2+CP2=DP2
即:△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.
证明:∵直线y=-2x-4
解: PC是⊙O的切线,
勾股(逆)定理
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑵判断在直线PC上是否存在点E,使得S△EOC=
4S△CDO,若存在,求出点E的坐标;若不存在,
请说明理由.
存
在
性
问
题
解:假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO,
∵E点在直线PC:y=-2x-4上,
∴当y0=4时有:
当y0=-4时有:
∴在直线PC上存在满足条件的E点,其的坐标为(-4,4) , (0,-4) .
抓住不变量
分类讨论
(复习课)
诊断补偿
1.如图, AB是⊙O的直径,∠ABC=45°,
AB=AC,AC是⊙O的切线吗 为什么?
3.如图,AB为直径,AC为切线,且BD=DC,求∠BAD多少
2.如图,Rt△ABC中,∠C=90°, AC=3cm,BC=4cm,以点C为圆心,2.4cm为半径的圆与AB有怎样的位置关系
B
C
O
A
B
A
C
B
D
C
O
A
1、知识点复习:
(1)切线的性质定理:
(2)切线的判定定理:
A
O
B
E
A
O
B
E
几何语言: ∵AB是⊙O的切线,E为切点 ∴AB⊥OE
圆的切线垂直于经过切点的半径。
几何语言:
∵AB⊥OE,
OE是⊙O的半径
∴AB是⊙O的切线
经过半径的外端且垂直于这条半径的直线是圆的切线。
(两个条件缺一不可)
圆的切线垂直于过切点的直径
经过直径的一端并且垂直于直径的直线是圆的切线.
直线L与圆相切
d = r
切线的性质
切线的判定
范例提炼
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点切线互相垂直,垂足为D. 求证:AC平分∠DAB
连结OC
∵CD是⊙O的切线∴OC⊥CD
又∵CD⊥AD∴OC∥AD ∴∠1=∠3
又∵OA=OC
∴∠2=∠3 ∴ ∠1=∠2
即AC平分∠DAB
证明:
小提示:连结圆心与切点是作辅助线常用的方法之一.
3
2
1
O
B
A
C
D
如图,AB为⊙O的直径, C为⊙O上一点,AD⊥CD,AC平分∠DAB.
求证: CD是⊙O的切线
变式1
变式2
如图,AB为⊙O的直径, AC平分∠DAB ,CD是⊙O的切线.
求证: AD⊥CD
3
2
1
B
O
A
C
D
变式导练
已知:如图, AB是⊙O的直径,⊙O过BE的中点C,CD⊥AE.
求证:DC是⊙O的切线.
证明:
连结AC,OC
∵AB为⊙O的直径∴AC⊥BE
又∵BC=EC∴AE=AB ∴∠1=∠2
又∵OA=OC∴∠2=∠3∴∠1=∠3
∴AE∥OC
∵CD⊥AE
∴DC⊥OC
∴DC是⊙O的切线.
3
2
1
B
O
A
C
D
E
B
O
A
C
D
B
O
A
C
D
E
能力提高
已知:AB是⊙O的直径, ⊙O过AC的中点,DE⊥BC,垂足为E.
⑴这些条件你能推出哪些正确的结论 (所连辅助线不要出现在结论中.不写推理过程,写出3个结论即可)
⑵当∠ABC为直角时,其他条件不变,除上述结论外,你还能推出哪些正确的结论 (要求将图画出,写出4个结论取即可)
E
D
C
O
B
A
如图,在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的圆O交AB于点E,⊙O切线EF交BC于点F
求证:EF⊥BC
A
E
B
D
C
F
O
(变式:作半径证垂直)
已知在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的圆O交AB于点E,EF⊥BC
求证:EF是⊙O的切线
证明:连结OE
∵梯形ABCD中,AB∥CD,AD=BC
∴∠A=∠B
∵OA=OE
∴∠A=∠OEA
∴∠OEA=∠B
∴OE∥BC
∵EF⊥BC
∴EF⊥OE
又OE是⊙O的半径
∴EF是⊙O的切线
9年衡阳市)如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60 .
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从A点出发沿着AB
方向运动,同时动点F以1cm/s的速度从B点出发
沿BC方向运动,设运动时间为t秒(0
交流评价
本节课你的收获是什么
切线的性质
圆的切线垂直于过切点的直径
切线的判定
经过直径的一端并且垂直于直径的直线是圆的切线.
直线L与圆相切
d = r
一种常用的辅助线
连结圆心与切点是作辅助线常用的方法之一.
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑴试猜想PC与⊙D的位置关系,并说明理由.
分析:做此类题,尤其强调
数形结合,同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证?联
想证明切线的两种方法。点
C在圆上,即证:∠DCP=90°
利用勾股及逆定理可得。
切
线
判
定
令x=0,得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5
又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20
在△CPD中, CD2+CP2=5+20=25, DP2=25
∴CD2+CP2=DP2
即:△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.
证明:∵直线y=-2x-4
解: PC是⊙O的切线,
勾股(逆)定理
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑵判断在直线PC上是否存在点E,使得S△EOC=
4S△CDO,若存在,求出点E的坐标;若不存在,
请说明理由.
存
在
性
问
题
解:假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO,
∵E点在直线PC:y=-2x-4上,
∴当y0=4时有:
当y0=-4时有:
∴在直线PC上存在满足条件的E点,其的坐标为(-4,4) , (0,-4) .
抓住不变量
分类讨论
