切线的判定
图片预览





文档简介
(共17张PPT)
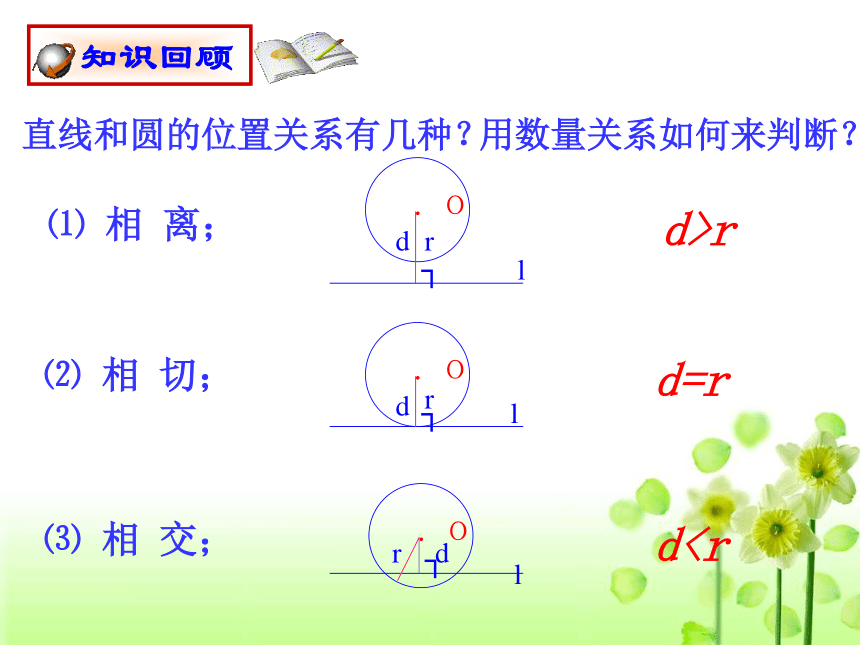
直线和圆的位置关系有几种?
知识回顾
⑴ 相 离;
⑵ 相 切;
⑶ 相 交;
dd=r
d>r
用数量关系如何来判断?
.O
l
┐
d
r
.O
l
┐
d
r
.O
l
┐
d
r
切 线 的 判 定
复 习
1.直线和圆有哪些位置关系?
2.什么叫相切?
3.我们学习过哪些切线的判断方法?
想一想
过圆0内一点作直线,这条直线与圆有什么位置关系?过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?
O
r
l
A
切线的判定定理 经过半径的外端并且垂直于这
条半径的直线是圆的切线。
∵ OA是半径,OA⊥l于A
∴ l是⊙O的切线。
几何符号表达:
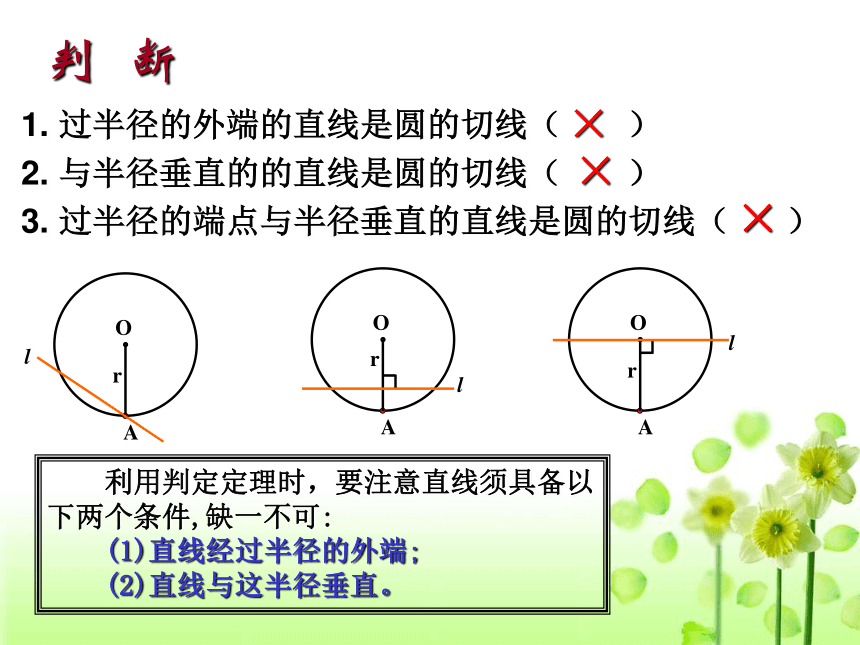
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。
判断一条直线是圆的切线,你现在会有多少种方法
有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
想一想
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连结OC(如图)。
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线。
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。
小 结
例1与例2的证法有何不同
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。
O
B
A
C
O
A
B
C
E
D
练 习
如图,△AOB中,OA=OB=10,∠AOB=120°,以O为圆心,
5为半径的⊙O与OA、OB相交。
求证:AB是⊙O的切线。
O
B
A
C
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴PE⊥OP。
∴PE为⊙0的切线。
如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
求证:PE是⊙O的切线。
练 习
O
A
B
C
E
P
练习3、如图4,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么?
图5
练习4、如图5,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B = 30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
例3、如图7,已知△ABC内接于⊙O,P是CB延长线上的一点,连结AP,且AP2 = PB·PC,试说明PA是⊙O的切线。
课堂小结
1. 判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2. 常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
思考题:如图,A是⊙O直径上的一点,OB是和这条直径垂直的半径,BA和⊙O相交于另一点C,过点C的直线和OA的延长线相交于点D,若DA = DC,问直线CD与⊙O 相切吗 为什么?
变题1:若将直线DA向上平行移至OB上,直线CD与⊙O 相切吗 为什么?
变题2:若将直线DA向上平行移至OB外,直线CD与⊙O 相切吗 为什么?
直线和圆的位置关系有几种?
知识回顾
⑴ 相 离;
⑵ 相 切;
⑶ 相 交;
d
d>r
用数量关系如何来判断?
.O
l
┐
d
r
.O
l
┐
d
r
.O
l
┐
d
r
切 线 的 判 定
复 习
1.直线和圆有哪些位置关系?
2.什么叫相切?
3.我们学习过哪些切线的判断方法?
想一想
过圆0内一点作直线,这条直线与圆有什么位置关系?过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?
O
r
l
A
切线的判定定理 经过半径的外端并且垂直于这
条半径的直线是圆的切线。
∵ OA是半径,OA⊥l于A
∴ l是⊙O的切线。
几何符号表达:
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。
判断一条直线是圆的切线,你现在会有多少种方法
有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
想一想
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连结OC(如图)。
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线。
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。
小 结
例1与例2的证法有何不同
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。
O
B
A
C
O
A
B
C
E
D
练 习
如图,△AOB中,OA=OB=10,∠AOB=120°,以O为圆心,
5为半径的⊙O与OA、OB相交。
求证:AB是⊙O的切线。
O
B
A
C
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴PE⊥OP。
∴PE为⊙0的切线。
如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
求证:PE是⊙O的切线。
练 习
O
A
B
C
E
P
练习3、如图4,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么?
图5
练习4、如图5,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B = 30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
例3、如图7,已知△ABC内接于⊙O,P是CB延长线上的一点,连结AP,且AP2 = PB·PC,试说明PA是⊙O的切线。
课堂小结
1. 判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2. 常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
思考题:如图,A是⊙O直径上的一点,OB是和这条直径垂直的半径,BA和⊙O相交于另一点C,过点C的直线和OA的延长线相交于点D,若DA = DC,问直线CD与⊙O 相切吗 为什么?
变题1:若将直线DA向上平行移至OB上,直线CD与⊙O 相切吗 为什么?
变题2:若将直线DA向上平行移至OB外,直线CD与⊙O 相切吗 为什么?
