2020-2021学年人教版 八年级下册数学19.2 一次函数 课时训练(含答案)
文档属性
| 名称 | 2020-2021学年人教版 八年级下册数学19.2 一次函数 课时训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 311.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:04:11 | ||
图片预览


文档简介
人教版 八年级下册数学19.2 一次函数 课时训练
一、选择题
1. 一次函数y=-2x+3的图象不经过的象限是( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2. (2019?陕西)若正比例函数的图象经过点O(a–1,4),则a的值为
A.–1 B.0
C.1 D.2
3. (2019?陕西)在平面直角坐标系中,将函数的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为
A.(2,0) B.(–2,0)
C.(6,0) D.(–6,0)
4. 如果一次函数的图象经过第一象限,且与轴负半轴相交,那么(??? )
A.??????? B.
C.? ?????? D.
5. (2019?沈阳)已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是
A.k<0 B.k<-1
C.k<1 D.k>-1
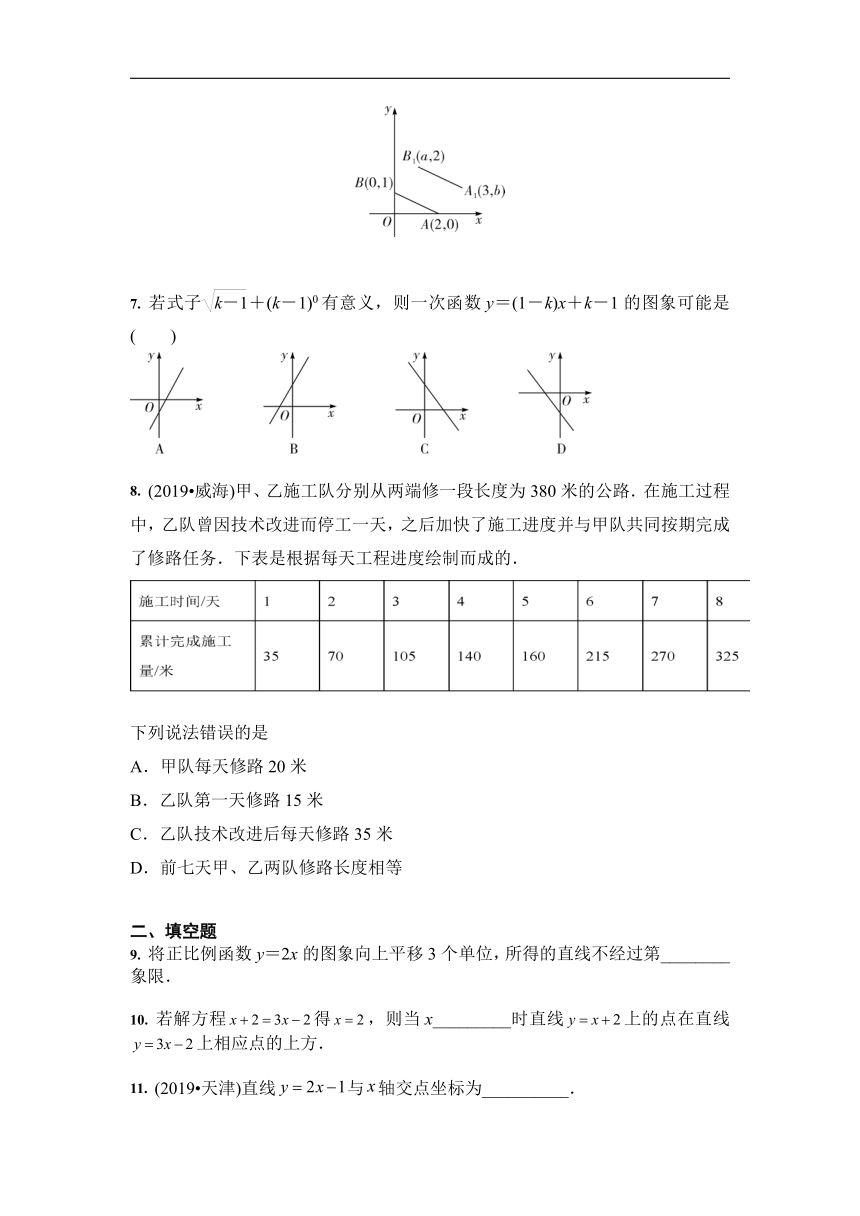
6. 如图,A、B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A. 2 B. 3 C. 4 D. 5
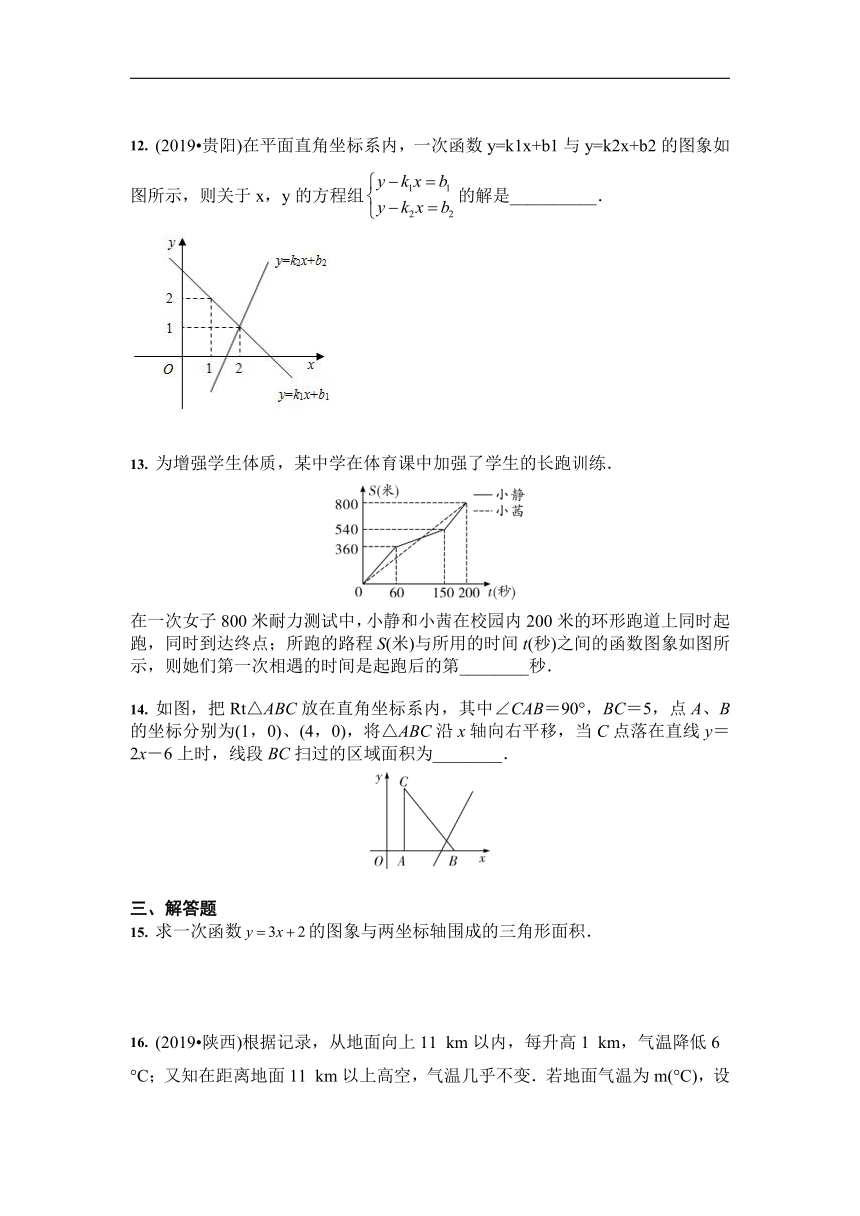
7. 若式子+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( )
8. (2019?威海)甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
下列说法错误的是
A.甲队每天修路20米
B.乙队第一天修路15米
C.乙队技术改进后每天修路35米
D.前七天甲、乙两队修路长度相等
二、填空题
9. 将正比例函数y=2x的图象向上平移3个单位,所得的直线不经过第________象限.
10. 若解方程得,则当x_________时直线上的点在直线上相应点的上方.
11. (2019?天津)直线与轴交点坐标为__________.
12. (2019?贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是__________.
13. 为增强学生体质,某中学在体育课中加强了学生的长跑训练.
在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第________秒.
14. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当C点落在直线y=2x-6上时,线段BC扫过的区域面积为________.
三、解答题
15. 求一次函数的图象与两坐标轴围成的三角形面积.
16. (2019?陕西)根据记录,从地面向上11 km以内,每升高1 km,气温降低6 °C;又知在距离地面11 km以上高空,气温几乎不变.若地面气温为m(°C),设距地面的高度为x(km)处的气温为y(°C)
(1)写出距地面的高度在11 km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26 °C时,飞机距离地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12 km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12 km时,飞机外的气温.
17. 某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运.如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人各连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?
18. 刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的镇;二分队因疲劳可在营地休息小时再往镇参加救灾.一分队出发后得知,唯一通往镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为千米/时.
⑴若二分队在营地不休息,问二分队几小时能赶到A镇?
⑵若二分队和一分队同时赶到镇,二分队应在营地休息几小时?
⑶下列图象中,①②分别描述一分队和二分队离镇的距离 (千米)和时间 (小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义.
人教版 八年级下册数学19.2 一次函数 课时训练-答案
一、选择题
1. 【答案】C 【解析】在一次函数y=-2x+3中,k=-2<0,图象经过第二、四象限;∵b=3>0,∴图象经过第一象限,则不经过第三象限.
2. 【答案】A
【解析】∵函数过O(a–1,4),∴,∴,故选A.
3. 【答案】B
【解析】根据函数图象平移规律,可知向上平移6个单位后得函数解析式应为,
此时与轴相交,则,
∴,即,
∴点坐标为(–2,0),
故选B.
4. 【答案】B
【解析】一次函数的图象经过第一象限,且与轴负半轴相交,画出大致图像,则,
5. 【答案】B
【解析】∵观察图象知:y随x的增大而减小,
∴k+1<0,
解得:k<-1,
故选B.
6. 【答案】A 【解析】由题图知:线段AB向右平移一个单位,再向上平移一个单位,即a=1,b=1,∴a+b=1+1=2.
7. 【答案】C 【解析】式子+(k-1)0有意义,则k>1,∴1-k<0,k-1>0,∴一次函数y=(1-k)x+k-1的图象经过第一、二、四象限.结合图象,故选C.
8. 【答案】D
【解析】由题意可得,
甲队每天修路:(米),故选项A正确;
乙队第一天修路:(米),故选项B正确;
乙队技术改进后每天修路:(米),故选项C正确;
前7天,甲队修路:米,乙队修路:米,故选项D错误,
故选D.
二、填空题
9. 【答案】四 【解析】根据平移规律“上加下减,左加右减”,将直线y=2x向上平移3个单位,得到的直线解析式为y=2x+3,因为2>0,3>0,所以图象过第一、第二和第三象限,故不经过第四象限.
10. 【答案】
【解析】列一元一次不等式或是画图象均可得出答案,上的点在直线上相应点的上方,即
11. 【答案】
【解析】∵当y=0时,2x–1=0,
∴x=,
∴直线与轴交点坐标为:,
故答案为:.
12. 【答案】
【解析】∵一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标为(2,1),
∴关于x,y的方程组的解是.
故答案为:.
13. 【答案】120 【解析】从函数图象可知,小茜是正比例函数图象,小静是分段函数图象,小静第二段函数图象与小茜的函数图象的交点的横坐标便是她们第一次相遇的时间.可求出小茜的函数解析式为S=4t,设小静第二段函数图象的解析式为S=kt+b,把(60,360)和(150,540)代入得,解得,∴此段函数解析式为S=2t+240,解方程组,得,故她们第一次相遇时间为起跑后第120秒.
14. 【答案】16 【解析】平移后如解图所示.∵点A、B的坐标分别为(1,0)、(4,0),∴AB=3,∵∠CAB=90°,BC=5,∴AC=4,∴A′C′=4,∵点C′在直线y=2x-6上,∴2x-6=4,解得x=5,即OA′=5,∴CC′=5-1=4,∴S?BCC′B′=4×4=16,即线段BC扫过的面积为16.
三、解答题
15. 【答案】
【解析】在函数中,
令,则,因此图象交y轴于点
令,则,解得,因此图象交x轴于点
∴函数与两坐标轴围成的三角形面积
16. 【答案】
(1)∵从地面向上11 km以内,每升高1 km,气温降低6 °C,地面气温为m(°C),距地面的高度为x(km)处的气温为y(°C),
∴y与x之间的函数表达式为:y=m-6x(0≤x≤11).
(2)将x=7,y=-26代入y=m-6x,得-26=m-42,
∴m=16,
∴当时地面气温为16 °C.
∵x=12>11,
∴y=16-6×11=-50(°C),
假如当时飞机距地面12 km时,飞机外的气温为-50 °C.
17. 【答案】
解:(1)设yB关于x的解析式为yB=k1x+b(k1≠0),
把E(1,0)和P(3,180)代入yB=k1x+b中,得:
,
解得,(3分)
∴yB关于x的解析式为yB=90x-90.(4分)
(2)设yA关于x的解析式为yA=k2x(k2≠0),由题意得:
180=3k2,即k2=60,
∴yA=60x,(6分)
当x=5时,yA=5×60=300(千克),
当x=6时,yB=90×6-90=450(千克)(8分)
450-300=150(千克).
答:如果A、B两种机器人各连续搬运5小时,那么B种机器人比A种机器人多搬运了150千克.(10分)
18. 【答案】
⑴8;⑵1小时或2小时;⑶合理的图像为(b)、(d)
【解析】⑴若二分队在营地不休息,则,速度为4千米/时,行至塌方处需(小时)
因为一分队到塌方处并打通道路需要(小时),故二分队在塌方处需停留0.5小时,所以二分队在营地不休息赶到A镇需(小时)
⑵一分队赶到A镇共需(小时)
①若二分队在塌方处需停留,则后20千米需与一分队同行,故,即,这与二分队在塌方处停留矛盾,舍去;
②若二分队在塌方处不停留,则,即,解得均符合题意.
答:二分队应在营地休息1小时或2小时.
⑶合理的图像为(b)、(d).
图像(b)表明二分队在营地休息时间过长(),后于一分队赶到A镇;
图像(d)表明二分队在营地休息时间恰当(),先于一分队赶到A镇.
一、选择题
1. 一次函数y=-2x+3的图象不经过的象限是( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2. (2019?陕西)若正比例函数的图象经过点O(a–1,4),则a的值为
A.–1 B.0
C.1 D.2
3. (2019?陕西)在平面直角坐标系中,将函数的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为
A.(2,0) B.(–2,0)
C.(6,0) D.(–6,0)
4. 如果一次函数的图象经过第一象限,且与轴负半轴相交,那么(??? )
A.??????? B.
C.? ?????? D.
5. (2019?沈阳)已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是
A.k<0 B.k<-1
C.k<1 D.k>-1
6. 如图,A、B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A. 2 B. 3 C. 4 D. 5
7. 若式子+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( )
8. (2019?威海)甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
下列说法错误的是
A.甲队每天修路20米
B.乙队第一天修路15米
C.乙队技术改进后每天修路35米
D.前七天甲、乙两队修路长度相等
二、填空题
9. 将正比例函数y=2x的图象向上平移3个单位,所得的直线不经过第________象限.
10. 若解方程得,则当x_________时直线上的点在直线上相应点的上方.
11. (2019?天津)直线与轴交点坐标为__________.
12. (2019?贵阳)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是__________.
13. 为增强学生体质,某中学在体育课中加强了学生的长跑训练.
在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第________秒.
14. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当C点落在直线y=2x-6上时,线段BC扫过的区域面积为________.
三、解答题
15. 求一次函数的图象与两坐标轴围成的三角形面积.
16. (2019?陕西)根据记录,从地面向上11 km以内,每升高1 km,气温降低6 °C;又知在距离地面11 km以上高空,气温几乎不变.若地面气温为m(°C),设距地面的高度为x(km)处的气温为y(°C)
(1)写出距地面的高度在11 km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为-26 °C时,飞机距离地面的高度为7 km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面12 km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12 km时,飞机外的气温.
17. 某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运.如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题:
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人各连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?
18. 刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的镇;二分队因疲劳可在营地休息小时再往镇参加救灾.一分队出发后得知,唯一通往镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为千米/时.
⑴若二分队在营地不休息,问二分队几小时能赶到A镇?
⑵若二分队和一分队同时赶到镇,二分队应在营地休息几小时?
⑶下列图象中,①②分别描述一分队和二分队离镇的距离 (千米)和时间 (小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义.
人教版 八年级下册数学19.2 一次函数 课时训练-答案
一、选择题
1. 【答案】C 【解析】在一次函数y=-2x+3中,k=-2<0,图象经过第二、四象限;∵b=3>0,∴图象经过第一象限,则不经过第三象限.
2. 【答案】A
【解析】∵函数过O(a–1,4),∴,∴,故选A.
3. 【答案】B
【解析】根据函数图象平移规律,可知向上平移6个单位后得函数解析式应为,
此时与轴相交,则,
∴,即,
∴点坐标为(–2,0),
故选B.
4. 【答案】B
【解析】一次函数的图象经过第一象限,且与轴负半轴相交,画出大致图像,则,
5. 【答案】B
【解析】∵观察图象知:y随x的增大而减小,
∴k+1<0,
解得:k<-1,
故选B.
6. 【答案】A 【解析】由题图知:线段AB向右平移一个单位,再向上平移一个单位,即a=1,b=1,∴a+b=1+1=2.
7. 【答案】C 【解析】式子+(k-1)0有意义,则k>1,∴1-k<0,k-1>0,∴一次函数y=(1-k)x+k-1的图象经过第一、二、四象限.结合图象,故选C.
8. 【答案】D
【解析】由题意可得,
甲队每天修路:(米),故选项A正确;
乙队第一天修路:(米),故选项B正确;
乙队技术改进后每天修路:(米),故选项C正确;
前7天,甲队修路:米,乙队修路:米,故选项D错误,
故选D.
二、填空题
9. 【答案】四 【解析】根据平移规律“上加下减,左加右减”,将直线y=2x向上平移3个单位,得到的直线解析式为y=2x+3,因为2>0,3>0,所以图象过第一、第二和第三象限,故不经过第四象限.
10. 【答案】
【解析】列一元一次不等式或是画图象均可得出答案,上的点在直线上相应点的上方,即
11. 【答案】
【解析】∵当y=0时,2x–1=0,
∴x=,
∴直线与轴交点坐标为:,
故答案为:.
12. 【答案】
【解析】∵一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标为(2,1),
∴关于x,y的方程组的解是.
故答案为:.
13. 【答案】120 【解析】从函数图象可知,小茜是正比例函数图象,小静是分段函数图象,小静第二段函数图象与小茜的函数图象的交点的横坐标便是她们第一次相遇的时间.可求出小茜的函数解析式为S=4t,设小静第二段函数图象的解析式为S=kt+b,把(60,360)和(150,540)代入得,解得,∴此段函数解析式为S=2t+240,解方程组,得,故她们第一次相遇时间为起跑后第120秒.
14. 【答案】16 【解析】平移后如解图所示.∵点A、B的坐标分别为(1,0)、(4,0),∴AB=3,∵∠CAB=90°,BC=5,∴AC=4,∴A′C′=4,∵点C′在直线y=2x-6上,∴2x-6=4,解得x=5,即OA′=5,∴CC′=5-1=4,∴S?BCC′B′=4×4=16,即线段BC扫过的面积为16.
三、解答题
15. 【答案】
【解析】在函数中,
令,则,因此图象交y轴于点
令,则,解得,因此图象交x轴于点
∴函数与两坐标轴围成的三角形面积
16. 【答案】
(1)∵从地面向上11 km以内,每升高1 km,气温降低6 °C,地面气温为m(°C),距地面的高度为x(km)处的气温为y(°C),
∴y与x之间的函数表达式为:y=m-6x(0≤x≤11).
(2)将x=7,y=-26代入y=m-6x,得-26=m-42,
∴m=16,
∴当时地面气温为16 °C.
∵x=12>11,
∴y=16-6×11=-50(°C),
假如当时飞机距地面12 km时,飞机外的气温为-50 °C.
17. 【答案】
解:(1)设yB关于x的解析式为yB=k1x+b(k1≠0),
把E(1,0)和P(3,180)代入yB=k1x+b中,得:
,
解得,(3分)
∴yB关于x的解析式为yB=90x-90.(4分)
(2)设yA关于x的解析式为yA=k2x(k2≠0),由题意得:
180=3k2,即k2=60,
∴yA=60x,(6分)
当x=5时,yA=5×60=300(千克),
当x=6时,yB=90×6-90=450(千克)(8分)
450-300=150(千克).
答:如果A、B两种机器人各连续搬运5小时,那么B种机器人比A种机器人多搬运了150千克.(10分)
18. 【答案】
⑴8;⑵1小时或2小时;⑶合理的图像为(b)、(d)
【解析】⑴若二分队在营地不休息,则,速度为4千米/时,行至塌方处需(小时)
因为一分队到塌方处并打通道路需要(小时),故二分队在塌方处需停留0.5小时,所以二分队在营地不休息赶到A镇需(小时)
⑵一分队赶到A镇共需(小时)
①若二分队在塌方处需停留,则后20千米需与一分队同行,故,即,这与二分队在塌方处停留矛盾,舍去;
②若二分队在塌方处不停留,则,即,解得均符合题意.
答:二分队应在营地休息1小时或2小时.
⑶合理的图像为(b)、(d).
图像(b)表明二分队在营地休息时间过长(),后于一分队赶到A镇;
图像(d)表明二分队在营地休息时间恰当(),先于一分队赶到A镇.
