指数函数的图像及性质(张家界桑植四中谷丽娟)
文档属性
| 名称 | 指数函数的图像及性质(张家界桑植四中谷丽娟) |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-25 08:19:17 | ||
图片预览






文档简介
(共26张PPT)
人教版高中高中必修一第二章第2节
指数函数的图像及性质
一、教学目标和重难点
(1)教学目标:
理解指数函数的概念,能画出具体指数函数的图象;在理解指数函数概念、性质的基础上,能应用所学知识解决简单的数学问题;使学生获得研究函数的规律和方法;培养学生主动学习、合作交流的意识。
(2)重难点:
课时1(函数图像及性质的探究)
教学重点:指数函数的概念、图像及性质
教学难点:底数的分类以及如何由图像解析式归纳指数函数的性质
课时2(指数函数图像及性质的应用)
教学重点:指数函数单调性的应用
教学难点:复合函数单调性的判定及区间求法
二、设计过程
●知识应用、提升总结
●师生互动、探究新知
●创设问题、导入新课
●新课导入
问题1:如果让1号同学准备2粒米,2号同学准备4粒米,3号同学准备6粒米,4号同学准备8粒米,5号同学准备10粒米,……按这样的规律,54号同学该准备多少米?
问题2:如果让1号同学准备2粒米,2号同学准备4粒米,3号同学准备8粒米,4号同学准备16粒米,5号同学准备25粒米,……按这样的规律,54号同学该准备多少米?
设计意图:用一个看似简单的实例,为引出指数函数的概念做准备;同时通过与一次函数的对比让学生感受指数函数的爆炸增长,激发学生学习新知的兴趣和欲望。
背景:54号同学所需准备的大米约重9.6亿吨,2010-2011年度我国大米产量创历史新高,大约为5.46亿吨。这就是说54号同学所需准备的大米比2010-2011年度我国全年的大米产量还多!
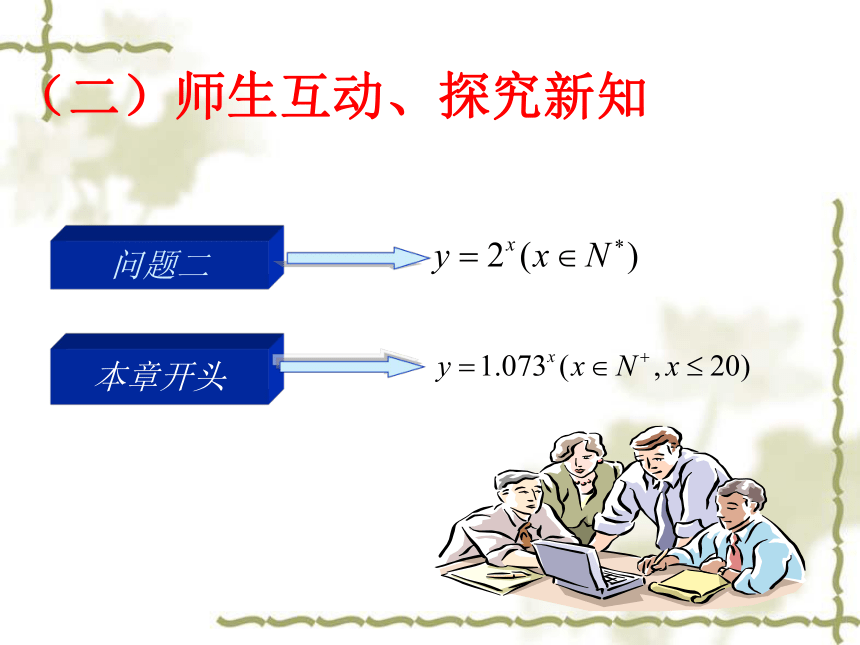
(二)师生互动、探究新知
问题二
本章开头
①这两个解析式有什么共同特征?
②它们能否构成函数?
③这种函数我们学过吗?如果没有,你能否根据该函数的特征给它起个恰当的名字?
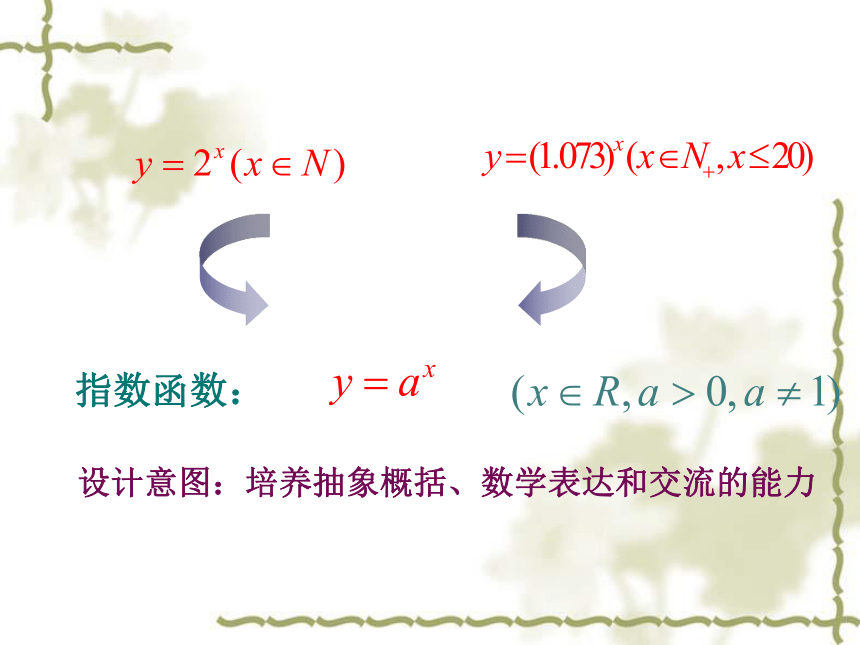
设计意图:引导学生从具体问题、实际问题中抽象出数学模型。学生对比已经学过一次函数、反比例函数、二次函数,发现,是一个新的函数模型,再让学生给这个新的函数命名,由此激发学生的学习兴趣。
设计意图:培养抽象概括、数学表达和交流的能力
指数函数:
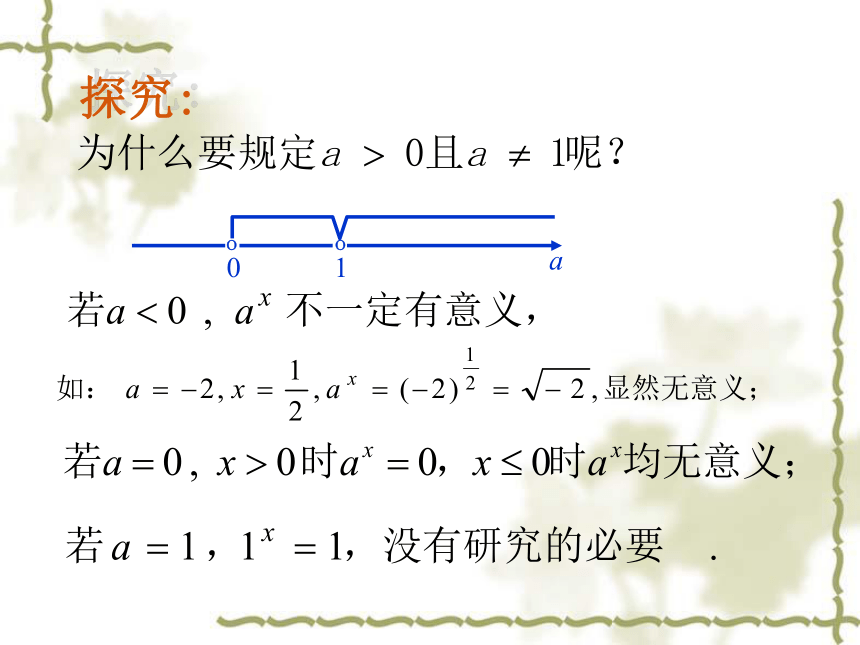
探究:
0
1
a
下列函数中,哪些是指数函数?
y =1x
我不是
我还不是
我是
我也不是
强调定义中“形如”的含义, 突出重点
指数函数图像及性质的探究:
①函数性质的研究一般可以包括哪些方面?
②函数可以怎么研究?用什么方法去研究?
设计意图:让学生在研究指数函数时有明确的目标
思考:
y=(1/2)x与y=2x的图象
P(x0,y0)
x0
P’(-x0,y0)
-x0
思考:
任意改变a的值图像会有怎样的变化呢?
思路一:互为倒数的图像关于y轴对称,图像可以分为两部分;
思路二:几何画板直接展示图形。
设计意图:引导学生由特殊 一般 特殊来逐步认识函数,了解函数,形成认识函数的一般思路,最后归纳性质。从而突出重点突破难点。
(1) a>1时,图象向右不断上升,并且
无限靠近x轴的负半轴;
0<a<1时,图象向右不断下降,并且
无限靠近x轴的正半轴.
(2) 对于多个指数函数来说,底数越大
的图象在y轴右侧的部分越高(简称:右
侧底大图高).
(3) 指数函数
关于y轴对称.
图像特征:
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
x > 0时,0< y <1
x < 0时,y > 1
x > 0时,y > 1
x < 0时,0< y <1
函数值变化情况
R
R
值 域
(0,+∞)
(0,+∞)
定义域
图 象
函 数
R
(0,+∞)
(0,1)
(三):知识应用、提升总结
1. 已知指数函数 的图象经过点 ,求 的值。
设计意图:通过本题加深学生对指数函数的理解,同时掌握指数变化的处理技巧,让学生明确底数是确定指数函数的要素,同时向学生渗透方程的思想。
根据本题,你能说出确定一个指数函数需要什么条件吗?
类型一:解析式和定义域的求法
2.求下列函数的定义域
①
②
设计意图:让学生掌握定义域的特点与求法
3.比较下列各题中两个值的大小:
① 1.72.5,1.73;
② 0.8-0.1,0.8-0.2;
③ 1.70.3,0.93.1.
类型二:运用指数函数单调性比较大小
设计意图:引导学生结合函数图形,利用区间内的单调性解决同底数幂的比较问题,并渗透数形结合与借助中间变量的思想。
变式训练: 将下列各数值按从小到大的顺序排列
设计意图:巩固第一象限右侧底大头高的应用.
5.说明下列函数图象与指数函数y=2x的图象关系,并画出 它们的图象:
类型三:指数函数图象的变换
归纳:向左平移a个单位得到f(x+a)的图象;
向右平移a个单位得到f(x-a)的图象;
向上平移a个单位得到f(x)+a的图象;
向下平移a个单位得到f(x)-a的图象
类型四:复合函数的单调性
方法一:图像法
方法二:换元法
知识小结
思想方法
数形结合
分类讨论
特殊
一般
特殊
指数函数
定义
图像
性质
特征
底数对性质的影响
综合应用
a >1、0<a<1
指数函数的图象和性质
1、指数函数的定义 3、指数函数的性质
2、指数函数的图象
在同一坐标系中分别作出 4、运用:
函数y = 2x 例题(略)
和y = (1\2)x 的图象 练习(略)
三、教学反思
教学中借助信息技术可以弥补传统教学在直观感、立体感和动态感方面的不足,可以很容易的化解教学难点、突破教学重点、提高课堂效率,本课使用几何画板可以动态地演示出指数函数的底数的动态过程,让学生直观观察底数对指数函数单调性的影响。
在教学过程中不断向学生渗透数学思想方法,让学生在活动中感受数学思想方法之美、体会数学思想方法之重要,部分学生还能自觉得运用这些数学思想方法去分析、思考问题。
人教版高中高中必修一第二章第2节
指数函数的图像及性质
一、教学目标和重难点
(1)教学目标:
理解指数函数的概念,能画出具体指数函数的图象;在理解指数函数概念、性质的基础上,能应用所学知识解决简单的数学问题;使学生获得研究函数的规律和方法;培养学生主动学习、合作交流的意识。
(2)重难点:
课时1(函数图像及性质的探究)
教学重点:指数函数的概念、图像及性质
教学难点:底数的分类以及如何由图像解析式归纳指数函数的性质
课时2(指数函数图像及性质的应用)
教学重点:指数函数单调性的应用
教学难点:复合函数单调性的判定及区间求法
二、设计过程
●知识应用、提升总结
●师生互动、探究新知
●创设问题、导入新课
●新课导入
问题1:如果让1号同学准备2粒米,2号同学准备4粒米,3号同学准备6粒米,4号同学准备8粒米,5号同学准备10粒米,……按这样的规律,54号同学该准备多少米?
问题2:如果让1号同学准备2粒米,2号同学准备4粒米,3号同学准备8粒米,4号同学准备16粒米,5号同学准备25粒米,……按这样的规律,54号同学该准备多少米?
设计意图:用一个看似简单的实例,为引出指数函数的概念做准备;同时通过与一次函数的对比让学生感受指数函数的爆炸增长,激发学生学习新知的兴趣和欲望。
背景:54号同学所需准备的大米约重9.6亿吨,2010-2011年度我国大米产量创历史新高,大约为5.46亿吨。这就是说54号同学所需准备的大米比2010-2011年度我国全年的大米产量还多!
(二)师生互动、探究新知
问题二
本章开头
①这两个解析式有什么共同特征?
②它们能否构成函数?
③这种函数我们学过吗?如果没有,你能否根据该函数的特征给它起个恰当的名字?
设计意图:引导学生从具体问题、实际问题中抽象出数学模型。学生对比已经学过一次函数、反比例函数、二次函数,发现,是一个新的函数模型,再让学生给这个新的函数命名,由此激发学生的学习兴趣。
设计意图:培养抽象概括、数学表达和交流的能力
指数函数:
探究:
0
1
a
下列函数中,哪些是指数函数?
y =1x
我不是
我还不是
我是
我也不是
强调定义中“形如”的含义, 突出重点
指数函数图像及性质的探究:
①函数性质的研究一般可以包括哪些方面?
②函数可以怎么研究?用什么方法去研究?
设计意图:让学生在研究指数函数时有明确的目标
思考:
y=(1/2)x与y=2x的图象
P(x0,y0)
x0
P’(-x0,y0)
-x0
思考:
任意改变a的值图像会有怎样的变化呢?
思路一:互为倒数的图像关于y轴对称,图像可以分为两部分;
思路二:几何画板直接展示图形。
设计意图:引导学生由特殊 一般 特殊来逐步认识函数,了解函数,形成认识函数的一般思路,最后归纳性质。从而突出重点突破难点。
(1) a>1时,图象向右不断上升,并且
无限靠近x轴的负半轴;
0<a<1时,图象向右不断下降,并且
无限靠近x轴的正半轴.
(2) 对于多个指数函数来说,底数越大
的图象在y轴右侧的部分越高(简称:右
侧底大图高).
(3) 指数函数
关于y轴对称.
图像特征:
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
x > 0时,0< y <1
x < 0时,y > 1
x > 0时,y > 1
x < 0时,0< y <1
函数值变化情况
R
R
值 域
(0,+∞)
(0,+∞)
定义域
图 象
函 数
R
(0,+∞)
(0,1)
(三):知识应用、提升总结
1. 已知指数函数 的图象经过点 ,求 的值。
设计意图:通过本题加深学生对指数函数的理解,同时掌握指数变化的处理技巧,让学生明确底数是确定指数函数的要素,同时向学生渗透方程的思想。
根据本题,你能说出确定一个指数函数需要什么条件吗?
类型一:解析式和定义域的求法
2.求下列函数的定义域
①
②
设计意图:让学生掌握定义域的特点与求法
3.比较下列各题中两个值的大小:
① 1.72.5,1.73;
② 0.8-0.1,0.8-0.2;
③ 1.70.3,0.93.1.
类型二:运用指数函数单调性比较大小
设计意图:引导学生结合函数图形,利用区间内的单调性解决同底数幂的比较问题,并渗透数形结合与借助中间变量的思想。
变式训练: 将下列各数值按从小到大的顺序排列
设计意图:巩固第一象限右侧底大头高的应用.
5.说明下列函数图象与指数函数y=2x的图象关系,并画出 它们的图象:
类型三:指数函数图象的变换
归纳:向左平移a个单位得到f(x+a)的图象;
向右平移a个单位得到f(x-a)的图象;
向上平移a个单位得到f(x)+a的图象;
向下平移a个单位得到f(x)-a的图象
类型四:复合函数的单调性
方法一:图像法
方法二:换元法
知识小结
思想方法
数形结合
分类讨论
特殊
一般
特殊
指数函数
定义
图像
性质
特征
底数对性质的影响
综合应用
a >1、0<a<1
指数函数的图象和性质
1、指数函数的定义 3、指数函数的性质
2、指数函数的图象
在同一坐标系中分别作出 4、运用:
函数y = 2x 例题(略)
和y = (1\2)x 的图象 练习(略)
三、教学反思
教学中借助信息技术可以弥补传统教学在直观感、立体感和动态感方面的不足,可以很容易的化解教学难点、突破教学重点、提高课堂效率,本课使用几何画板可以动态地演示出指数函数的底数的动态过程,让学生直观观察底数对指数函数单调性的影响。
在教学过程中不断向学生渗透数学思想方法,让学生在活动中感受数学思想方法之美、体会数学思想方法之重要,部分学生还能自觉得运用这些数学思想方法去分析、思考问题。
