5.7三角函数的应用(第二课时) 课件(27张PPT)
文档属性
| 名称 | 5.7三角函数的应用(第二课时) 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 00:00:00 | ||
图片预览






文档简介
5.7 三角函数的应用
第二课时
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
新知探究
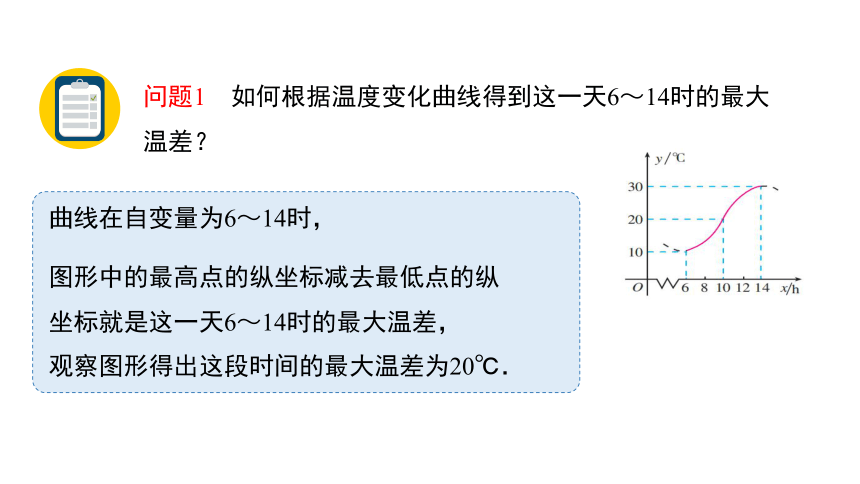
例1 如图,某地一天从6~14时的温度变化曲线近似满足函数
曲线在自变量为6~14时,
图形中的最高点的纵坐标减去最低点的纵坐标就是这一天6~14时的最大温差,
观察图形得出这段时间的最大温差为20℃.
新知探究
问题1 如何根据温度变化曲线得到这一天6~14时的最大温差?
新知探究
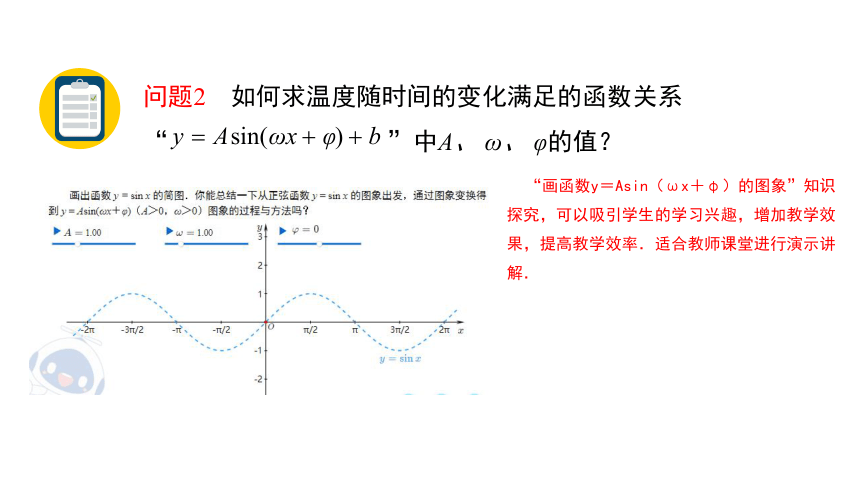
问题2 如何求温度随时间的变化满足的函数关系“ ”中A、 ω、 φ的值?
“画函数y=Asin(ωx+φ)的图象”知识探究,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.适合教师课堂进行演示讲解.
A为最大值减去最小值的差的一半,
ω可以利用半周期为14-6=8建立方程得解,
φ可以利用特殊值求得.
所求解析式为
新知探究
问题2 如何求温度随时间的变化满足的函数关系“ ”中A、 ω、 φ的值?
新知探究
★资源名称:【情景演示】潮汐运动
★使用说明:本资源通过生活中有关海水潮汐运动的展示,激发学生学习的兴趣.也体现数学来源于生活,又服务于生活.适合教师课堂展示播放.
注:此图片为“情景视频”缩略图,如需使用资源,请于资源库调用.
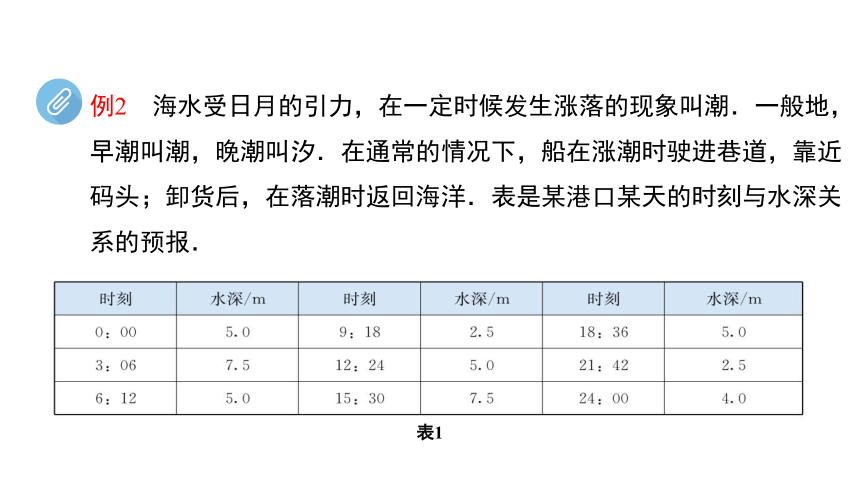
表1
新知探究
例2 海水受日月的引力,在一定时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常的情况下,船在涨潮时驶进巷道,靠近码头;卸货后,在落潮时返回海洋.表是某港口某天的时刻与水深关系的预报.
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001 m).
(2)一条货船的吃水深度(船底与水面的距离)为4 m,安全条例规定至少要有1.5 m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
(3)若船的吃水深度为4 m,安全间隙为1.5 m,该船在两点开始卸货,吃水深度以0.3 m/h的速度减少,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
新知探究
观察表格中数据可以看出,
水深的变化具有周期性,
根据表中数据画出散点图(如图).
从散点图的形状可以判断,
y=Asin(ωx+φ)+h的函数来刻画,
这个港口的水深y与时间x的关系可以用形如
从数据和图形可以得出:
新知探究
问题3 观察表1中的数据,你发现了什么规律?根据数据做出散点图,观察图形,你可以用怎样的函数模型来刻画其中的规律?请试着完成(1)的解答.
A=2.5,h=5,T=12.4,φ=0,
所以个港口的水深与时间的关系可用函数
近似描述.
由 得 .
新知探究
问题3 观察表1中的数据,你发现了什么规律?根据数据做出散点图,观察图形,你可以用怎样的函数模型来刻画其中的规律?请试着完成(1)的解答.
整点时的水深的近似值为下表
新知探究
从函数的解析式来看,满足怎样的条件时,该船能够进入港口?
从图象上看呢?
答案:货船需要的安全水深为4+1.5=5.5 m.
该船能够进入港口;
从函数的解析式来看,满足y≥5.5即 ,
从图象上看,
该船能够进入港口.
就是函数 的图象在直线y=5.5上方时,
新知探究
问题4 (2)中,货船需要的安全深度是多少?
答案:
求得交点的横坐标分别为:
新知探究
从图象上看呢?
问题4 (2)中,货船需要的安全深度是多少?
从函数的解析式来看,满足怎样的条件时,该船能够进入港口?
事实上为了安全,进港时间要比算出的时间推后一些,
出港时间要比算出的时间提前一些,
这样才能保证货船始终在安全水域.
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;
或在下午13时左右进港,下午18时左右出港.
每次可以在港口停留5小时左右.
新知探究
问题5 可以将A,B,C,D点的横坐标作为进出港时间吗?为什么?
设在x h时货船的安全水深为y m,
那么y=5.5-0.3(x-2)(x≥2).
从函数的解析式来看,满足 y≥5.5-0.3(x-2),
即
时,该船能够进入港口;
从图象上看,就是函数 的图象在直线
上方时,该船能够进入港口.
新知探究
问题6 (3)中,设在x h时货船的安全水深为y m,y与时间x满足怎样的函数关系?从解析式来看,满足怎样的条件时,该船必须停止卸货?从图象上看呢?
可以看到在6~8时之间两个函数只有一个交点P,
求得P点的横坐标为xP≈7.016.
新知探究
问题6 (3)中,设在x h时货船的安全水深为y m,y与时间x满足怎样的函数关系?从解析式来看,满足怎样的条件时,该船必须停止卸货?从图象上看呢?
为了安全,船停止卸货驶向安全水域的时间要比算出的时间提前一些.
因此为了安全,货船最好在6.6时停止卸货,将船驶向较深的水域.
新知探究
问题7 在船的安全水深正好等于港口水深时停止卸货可以吗?
建立三角函数模型解决实际问题的基本步骤:
①搜集数据,做出散点图;
②观察散点图并进行函数拟合,获得具体的函数模型;
③利用这个函数模型解决相应的实际问题.需要注意的是,从数学模型中得到的答案还要根据实际情况检验它是否可行.
新知探究
问题8 通过本题的研究,你能概括出建立三角函数模型解决实际问题的基本步骤和需要注意的问题吗?
练习1 图为一向右传播的绳波在某一时刻绳子各店的位置图,经过 周期后,乙点的位置将移至何处?
乙点的位置将移至它关于x轴的对称点处.
新知探究
练习2 从出生之日起,人的情绪、体力、智力等状况就呈周期性变化,根据心理学统计,人体节律分为体力节律,情绪节律,智力节律三种,这些节律的时间周期分别为23天,28天,33天.每个节律周期又分为高潮期,临界日,低潮期三个阶段.节律周期的半数为临界日,临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),请根据自己的出生日期,绘制自己的体力,情绪,智力曲线,并预测本学期期末考试期间,你在体力,情绪,智力方面会有怎样的表现,需要注意哪些问题?
新知探究
解答:由题可知,三个节律曲线的函数模型为y=Asin ωx的形式,
为了研究的方便,我们可以统一设A=10,
象进行分析.
数得到三个自变量,
新知探究
计算从出生日到本学期期末考试三天的天
观察相应变量区间的三个节律曲线的函数图
以出生日为自变量1,
由节律的时间周期分
别为23天,28天,33天可得相应解析式中的ω值分别为 .
归纳小结
问题9 生活中哪类问题可以利用三角函数模型解决?利用三角函数解决实际问题的一般步骤是怎样的?你能够将本节课所学内容画出一个知识结构图吗?其中涉及到哪些数学思想?通过本节课的学习,你还有哪些收获?
实际问题
三角函数模型
解决三角函数问题
联系实际解决问题
周期性
收集数据画散点图
观察图形函数拟合
周期性
作业布置
作业:教科书习题5.7第3,4题.
目标检测
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t/h
0
3
6
9
12
15
18
21
24
y/m
1.0
1.4
1.0
0.6
1.0
1.4
0.9
0.4
1.0
练
某“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度y(m)随着时间t(0≤t≤24,单位:h)周期性变化.为了了解其变化规律,该队观察若干天后,得到每天各时刻t的浪高数据的平均值如下表:
目标检测
(1)试画出散点图;
(2)观察散点图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)+b中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定当浪高不低于0.8 m时才进行训练,试安排合适的训练时间段.
目标检测
(2)由散点图可知,选择y=Asin(ωt+φ)+b函数模型较为合适.
(3)在11 h~19 h进行训练较为合适.
解:(1)如图;
再见
第二课时
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
新知探究
例1 如图,某地一天从6~14时的温度变化曲线近似满足函数
曲线在自变量为6~14时,
图形中的最高点的纵坐标减去最低点的纵坐标就是这一天6~14时的最大温差,
观察图形得出这段时间的最大温差为20℃.
新知探究
问题1 如何根据温度变化曲线得到这一天6~14时的最大温差?
新知探究
问题2 如何求温度随时间的变化满足的函数关系“ ”中A、 ω、 φ的值?
“画函数y=Asin(ωx+φ)的图象”知识探究,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.适合教师课堂进行演示讲解.
A为最大值减去最小值的差的一半,
ω可以利用半周期为14-6=8建立方程得解,
φ可以利用特殊值求得.
所求解析式为
新知探究
问题2 如何求温度随时间的变化满足的函数关系“ ”中A、 ω、 φ的值?
新知探究
★资源名称:【情景演示】潮汐运动
★使用说明:本资源通过生活中有关海水潮汐运动的展示,激发学生学习的兴趣.也体现数学来源于生活,又服务于生活.适合教师课堂展示播放.
注:此图片为“情景视频”缩略图,如需使用资源,请于资源库调用.
表1
新知探究
例2 海水受日月的引力,在一定时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常的情况下,船在涨潮时驶进巷道,靠近码头;卸货后,在落潮时返回海洋.表是某港口某天的时刻与水深关系的预报.
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001 m).
(2)一条货船的吃水深度(船底与水面的距离)为4 m,安全条例规定至少要有1.5 m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
(3)若船的吃水深度为4 m,安全间隙为1.5 m,该船在两点开始卸货,吃水深度以0.3 m/h的速度减少,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
新知探究
观察表格中数据可以看出,
水深的变化具有周期性,
根据表中数据画出散点图(如图).
从散点图的形状可以判断,
y=Asin(ωx+φ)+h的函数来刻画,
这个港口的水深y与时间x的关系可以用形如
从数据和图形可以得出:
新知探究
问题3 观察表1中的数据,你发现了什么规律?根据数据做出散点图,观察图形,你可以用怎样的函数模型来刻画其中的规律?请试着完成(1)的解答.
A=2.5,h=5,T=12.4,φ=0,
所以个港口的水深与时间的关系可用函数
近似描述.
由 得 .
新知探究
问题3 观察表1中的数据,你发现了什么规律?根据数据做出散点图,观察图形,你可以用怎样的函数模型来刻画其中的规律?请试着完成(1)的解答.
整点时的水深的近似值为下表
新知探究
从函数的解析式来看,满足怎样的条件时,该船能够进入港口?
从图象上看呢?
答案:货船需要的安全水深为4+1.5=5.5 m.
该船能够进入港口;
从函数的解析式来看,满足y≥5.5即 ,
从图象上看,
该船能够进入港口.
就是函数 的图象在直线y=5.5上方时,
新知探究
问题4 (2)中,货船需要的安全深度是多少?
答案:
求得交点的横坐标分别为:
新知探究
从图象上看呢?
问题4 (2)中,货船需要的安全深度是多少?
从函数的解析式来看,满足怎样的条件时,该船能够进入港口?
事实上为了安全,进港时间要比算出的时间推后一些,
出港时间要比算出的时间提前一些,
这样才能保证货船始终在安全水域.
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;
或在下午13时左右进港,下午18时左右出港.
每次可以在港口停留5小时左右.
新知探究
问题5 可以将A,B,C,D点的横坐标作为进出港时间吗?为什么?
设在x h时货船的安全水深为y m,
那么y=5.5-0.3(x-2)(x≥2).
从函数的解析式来看,满足 y≥5.5-0.3(x-2),
即
时,该船能够进入港口;
从图象上看,就是函数 的图象在直线
上方时,该船能够进入港口.
新知探究
问题6 (3)中,设在x h时货船的安全水深为y m,y与时间x满足怎样的函数关系?从解析式来看,满足怎样的条件时,该船必须停止卸货?从图象上看呢?
可以看到在6~8时之间两个函数只有一个交点P,
求得P点的横坐标为xP≈7.016.
新知探究
问题6 (3)中,设在x h时货船的安全水深为y m,y与时间x满足怎样的函数关系?从解析式来看,满足怎样的条件时,该船必须停止卸货?从图象上看呢?
为了安全,船停止卸货驶向安全水域的时间要比算出的时间提前一些.
因此为了安全,货船最好在6.6时停止卸货,将船驶向较深的水域.
新知探究
问题7 在船的安全水深正好等于港口水深时停止卸货可以吗?
建立三角函数模型解决实际问题的基本步骤:
①搜集数据,做出散点图;
②观察散点图并进行函数拟合,获得具体的函数模型;
③利用这个函数模型解决相应的实际问题.需要注意的是,从数学模型中得到的答案还要根据实际情况检验它是否可行.
新知探究
问题8 通过本题的研究,你能概括出建立三角函数模型解决实际问题的基本步骤和需要注意的问题吗?
练习1 图为一向右传播的绳波在某一时刻绳子各店的位置图,经过 周期后,乙点的位置将移至何处?
乙点的位置将移至它关于x轴的对称点处.
新知探究
练习2 从出生之日起,人的情绪、体力、智力等状况就呈周期性变化,根据心理学统计,人体节律分为体力节律,情绪节律,智力节律三种,这些节律的时间周期分别为23天,28天,33天.每个节律周期又分为高潮期,临界日,低潮期三个阶段.节律周期的半数为临界日,临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),请根据自己的出生日期,绘制自己的体力,情绪,智力曲线,并预测本学期期末考试期间,你在体力,情绪,智力方面会有怎样的表现,需要注意哪些问题?
新知探究
解答:由题可知,三个节律曲线的函数模型为y=Asin ωx的形式,
为了研究的方便,我们可以统一设A=10,
象进行分析.
数得到三个自变量,
新知探究
计算从出生日到本学期期末考试三天的天
观察相应变量区间的三个节律曲线的函数图
以出生日为自变量1,
由节律的时间周期分
别为23天,28天,33天可得相应解析式中的ω值分别为 .
归纳小结
问题9 生活中哪类问题可以利用三角函数模型解决?利用三角函数解决实际问题的一般步骤是怎样的?你能够将本节课所学内容画出一个知识结构图吗?其中涉及到哪些数学思想?通过本节课的学习,你还有哪些收获?
实际问题
三角函数模型
解决三角函数问题
联系实际解决问题
周期性
收集数据画散点图
观察图形函数拟合
周期性
作业布置
作业:教科书习题5.7第3,4题.
目标检测
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t/h
0
3
6
9
12
15
18
21
24
y/m
1.0
1.4
1.0
0.6
1.0
1.4
0.9
0.4
1.0
练
某“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度y(m)随着时间t(0≤t≤24,单位:h)周期性变化.为了了解其变化规律,该队观察若干天后,得到每天各时刻t的浪高数据的平均值如下表:
目标检测
(1)试画出散点图;
(2)观察散点图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)+b中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定当浪高不低于0.8 m时才进行训练,试安排合适的训练时间段.
目标检测
(2)由散点图可知,选择y=Asin(ωt+φ)+b函数模型较为合适.
(3)在11 h~19 h进行训练较为合适.
解:(1)如图;
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
