2019-2020学年黑龙江省哈尔滨六十九中八年级(下)期中数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨六十九中八年级(下)期中数学试卷(五四学制) (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 08:30:54 | ||
图片预览

文档简介
2019-2020学年黑龙江省哈尔滨六十九中八年级(下)期中数学试卷(五四学制)
一、选择题(共10小题).
1.下列四个图象中,y不是x的函数图象的是( )
A. B.
C. D.
2.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
3.下列各点在函数y=﹣的图象上的是( )
A.(2,1) B.(﹣2,0) C.(2,0) D.(﹣2,1)
4.下列说法不能得到直角三角形的( )
A.三个角度之比为1:2:3的三角形
B.三个边长之比为3:4:5的三角形
C.三个边长之比为8:16:17的三角形
D.三个角度之比为1:1:2的三角形
5.将一根24cm的筷子,置于底面直径为15cm,高8cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是( )
A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm
6.平行四边形的两条对角线长分别是x,y,一边长为12,则x,y可能是下列各组中的( )
A.8与14 B.10与14 C.18与20 D.10与38
7.下列说法不能判断是正方形的是( )
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
8.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为40cm,钟面数字2在长方形的顶点处,则长方形的长为( )cm.
A.80 B.60 C.50 D.40
9.如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A. B. C.1 D.
10.在全民健身环城越野赛中,甲、乙两名选手各自的行程y(km)随时间t(h)变化的图象(全程)如图所示.有下列说法:①起跑后2h内,甲在乙的前面;②第1h时两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共10小题).
11.函数y=中自变量x的取值范围是 .
12.已知矩形周长为10,则矩形的长y与宽x之间的函数关系式为 .
13.在△ABC中,若a2+b2=25,a2b2=7,c=5,则最长边上的高为 .
14.三角形的三边长分别是4cm,5cm,6cm,则连结三边中点所围成的三角形的周长是 cm.
15.如图,以正方形ABCD的边AB为一边向外作等边△ABE,则∠BED= °.
16.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上点C1处,则CD的长为 .
17.如图,在△ABC中,D、E、F分别是BC、AC、AB边的中点,AH⊥BC于H,∠ACH=60°,CH=,则线段DF的长是 .
18.如图,在平行四边形ABCD中,AB=4,BC=6,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=60°,则平行四边形的面积是 .
19.矩形的一个角的平分线分一边为3cm和4cm两部分,则这个矩形的对角线的长为 cm.
20.如图,P为矩形ABCD内一点,PB=PC,∠BPC=90°,∠PAB=75°,若AB=11,PD=14,则PA的长为 .
三、解答题(21、22题每题7分,23、24题每题8分,25-27题每题10分,共60分)
21.如图,小明想测量学校旗杆AB的高度,他采用如下方法:先将旗杆上的绳子垂到地面,还多1米,然后将绳子下端拉直,使它的末端刚好接触地面,测得绳子下端C离旗杆底部B点5米,请你计算一下旗杆的高度.
22.在正方形网格中,每个小正方形的边长为1.
(1)在图1中,画矩形ABCD(非正方形)使它的面积为10,要求它的顶点均在格点上.并直接写出图1中矩形ABCD的对角线长为 .
(2)在图2中,画正方形ABCD,使它的面积为13,要求它的顶点均在格点上.
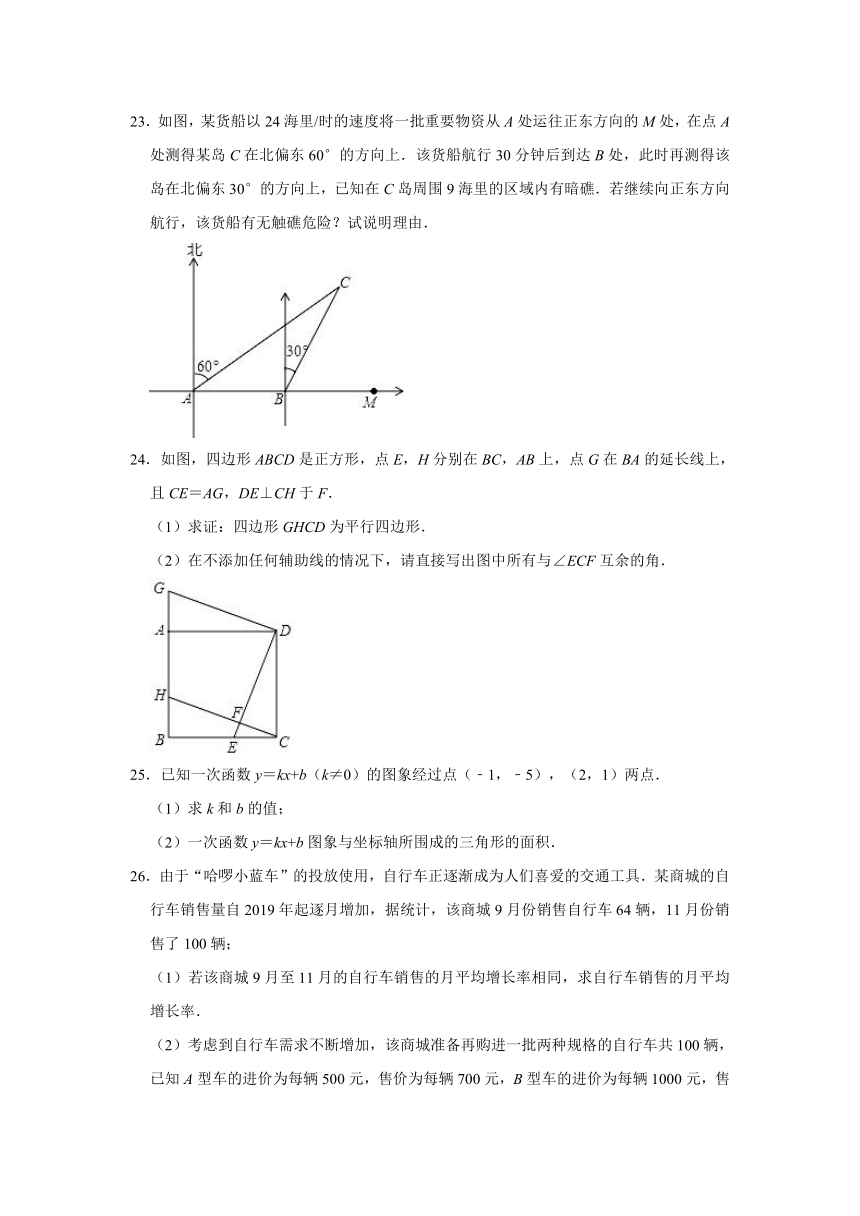
23.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,已知在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
24.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.
(1)求证:四边形GHCD为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.
25.已知一次函数y=kx+b(k≠0)的图象经过点(﹣1,﹣5),(2,1)两点.
(1)求k和b的值;
(2)一次函数y=kx+b图象与坐标轴所围成的三角形的面积.
26.由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自2019年起逐月增加,据统计,该商城9月份销售自行车64辆,11月份销售了100辆;
(1)若该商城9月至11月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共100辆,已知A型车的进价为每辆500元,售价为每辆700元,B型车的进价为每辆1000元,售价为每辆1300元.假设所购进车辆全部售完,为使利润不低于26000元,该商城购进A型车不超过多少辆?
27.已知:菱形ABCD,点E在线段BC上,连接DE,点F在线段AB上,连接CF、DF,CF与DE交于点G,将菱形ABCD沿DF翻折,点A恰好落在点G上.
(1)求证:CD=CF;
(2)设∠CED=x,∠DCF=y,求y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当x=45°时,以CD为底边作等腰△CDK,顶角顶点K在菱形ABCD的内部,连接GK,若GK∥CD,CD=4时,求线段KG的长.
28.已知:如图,在平面直角坐标系中,点A的坐标为(6,0),AB=6,点P从点O出发沿线段OA向终点A运动,点P的运动速度是每秒2个单位长度,点D是线段OA的中点.
(1)求点B的坐标;
(2)设点P的运动时间为点t秒,△BDP的面积为S,求S与t的函数关系式;
(3)当点P与点D重合时,连接BP,点E在线段AB上,连接PE,当∠BPE=2∠OBP时,求点E的坐标.
参考答案
一、选择题(共10小题).
1.下列四个图象中,y不是x的函数图象的是( )
A. B.
C. D.
解:根据函数定义,如果在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应.选项A、B、C中对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应,所以y是x的函数;而D中的y的值不具有唯一性,所以不是函数图象.
故选:D.
2.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
解:在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则v、t是变量,s是常量,
故选:C.
3.下列各点在函数y=﹣的图象上的是( )
A.(2,1) B.(﹣2,0) C.(2,0) D.(﹣2,1)
解:∵函数解析式为y=﹣,
把四个选项的坐标依次代入函数解析式,仅选项D的坐标(﹣2,1)在函数y=﹣的图象上,
∴D选项符合题意,A、B、C选项不符合题意,
故选:D.
4.下列说法不能得到直角三角形的( )
A.三个角度之比为1:2:3的三角形
B.三个边长之比为3:4:5的三角形
C.三个边长之比为8:16:17的三角形
D.三个角度之比为1:1:2的三角形
解:A、最大角=180°×=90°,故为直角三角形;
B、32+42=52,故为直角三角形;
C、82+162≠172,故不为直角三角形;
D、最大角=180°×=90°,故为直角三角形.
故选:C.
5.将一根24cm的筷子,置于底面直径为15cm,高8cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是( )
A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm
解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24﹣8=16(cm);
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=15cm,BD=8cm,
∴AB==17(cm),
所以h的取值范围是:8cm≤h≤17cm.
故选:C.
6.平行四边形的两条对角线长分别是x,y,一边长为12,则x,y可能是下列各组中的( )
A.8与14 B.10与14 C.18与20 D.10与38
解:∵四边形ABCD是平行四边形,
∴OA=OC=AC=x,OB=OD=BD=y,BC=12,
根据三角形三边关系可得:x+y>12,|y﹣x|<12,
即:x+y>24,|x﹣y|<24,
然后代入数值检验.即可得C符合要求.
故选:C.
7.下列说法不能判断是正方形的是( )
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
解:A.对角线互相垂直且相等的平行四边形是正方形,故A选项不符合题意;
B.对角线互相垂直的矩形是正方形,故B选项不符合题意;
C.对角线相等的菱形是正方形,故C选项不符合题意;
D.对角线互相垂直平分的四边形是菱形,菱形不一定是正方形,故D选项符合题意;
故选:D.
8.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为40cm,钟面数字2在长方形的顶点处,则长方形的长为( )cm.
A.80 B.60 C.50 D.40
解:由题意知∠AOC=2∠BOC,
∵∠AOC+∠BOC=90°,
∴∠BOC=30°,∠AOC=60°,
∴OB=BC,
∴矩形ABCD长是宽的倍,
∴长方形的长是40cm;
故选:D.
9.如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A. B. C.1 D.
解:过F作FH⊥AE于H,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE,
∴DE=BF,
∴AF=3﹣DE,
∴AE=,
∵∠FHA=∠D=∠DAF=90°,
∴∠AFH+∠HAF=∠DAE+∠FAH=90°,
∴∠DAE=∠AFH,
∴△ADE∽△AFH,
∴,
∴AE=AF,
∴=3﹣DE,
∴DE=,
故选:D.
解法二:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAH=∠AED,
∵∠ADE=∠AHF=∠DAF=90°,AD=2,FH=2,
∴AD=FH,
∴△ADE≌△FAH,
∴AF=AE,
∵AE∥CF,AF∥EC,
∴四边形AECF是平行四边形,
∵AF=AE,
∴四边形AECF是菱形,
设DE=x,则BF=x,CE=CF=3﹣x,
在Rt△BCF中,(3﹣x)2=x2+22,
∴x=.
故选:D.
10.在全民健身环城越野赛中,甲、乙两名选手各自的行程y(km)随时间t(h)变化的图象(全程)如图所示.有下列说法:①起跑后2h内,甲在乙的前面;②第1h时两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
解:①由横坐标看出,起跑后1小时内,甲在乙的前面,故①错误;
②由纵坐标看出,第一小时两人都跑了10千米,故②正确;
③由横坐标看出乙比甲先到达终点,故③错误;
④由纵坐标看出两人都跑了20千米,故④正确;
故选:B.
二、填空题(每小题3分,共30分)
11.函数y=中自变量x的取值范围是 x≠1 .
解:根据题意得:x﹣1≠0,
解得:x≠1.
故答案是:x≠1.
12.已知矩形周长为10,则矩形的长y与宽x之间的函数关系式为 y=5﹣x .
解:∵矩形周长=(长+宽)×2,
∴y=﹣x=5﹣x,
故答案为:y=5﹣x.
13.在△ABC中,若a2+b2=25,a2b2=7,c=5,则最长边上的高为 .
解:∵a2+b2=25,c=5,
∴a2+b2=c2,
∴△ABC是直角三角形,
∵a2b2=7,
∴ab=,
∴S△ACB==,
设最长边上的高为x,
则?x×5=,
解得:x=,
故答案为:.
14.三角形的三边长分别是4cm,5cm,6cm,则连结三边中点所围成的三角形的周长是 7.5 cm.
解:D,E,F分别是△ABC的三边的中点,
则DE=AC=2.5,DF=BC=3,EF=AB=2,
∴△DEF的周长=DE+DF+EF=2.5+3+2=7.5(cm).
故答案为:7.5.
15.如图,以正方形ABCD的边AB为一边向外作等边△ABE,则∠BED= 45 °.
解:在正方形ABCD中,AB=AD,∠BAD=90°,
在等边△ABE中,AB=AE,∠BAE=∠AEB=60°,
在△ADE中,AD=AE,∠DAE=∠BAD+∠BAE=90°+60°=150°,
所以,∠AED=(180°﹣150°)=15°,
∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°.
故答案为:45.
16.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上点C1处,则CD的长为 3 .
解:∵∠C=90°,AC=6,AB=10,
∴BC=8,
由折叠可得AC1=AC=6,
∴BC1=10﹣6=4,
设CD=x,则BD=8﹣x,
在Rt△DBC1中,42+x2=(8﹣x)2,
∴x=3.
∴CD=3,
故答案为:3.
17.如图,在△ABC中,D、E、F分别是BC、AC、AB边的中点,AH⊥BC于H,∠ACH=60°,CH=,则线段DF的长是 .
解:∵AH⊥BC,∠ACH=60°,
∴∠HAC=30°,
∴AC=2CH=,
∵D、F分别是BC、AB边的中点,
∴DF=AC=,
故答案为:.
18.如图,在平行四边形ABCD中,AB=4,BC=6,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=60°,则平行四边形的面积是 12 .
解:∵AE⊥BC于点E,AF⊥CD于点F,
∴∠AEC=90°,∠AFC=90°,
又∵∠EAF=60°,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠B=∠D=60°,
∴∠BAE=∠DAF=30°,
∵AB=4,BC=6,
∴BE=2,
∴AE==2,
∴平行四边形的面积是:2×6=12.
故答案为:12.
19.矩形的一个角的平分线分一边为3cm和4cm两部分,则这个矩形的对角线的长为 或 cm.
解:如图所示:
∵△ABCD是平行四边形,
∴AD∥BC,AC=BD,∠C=90°,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE;
当AE=4cm时,AB=4cm;AD=7cm,
∴BD===(cm);
当AE=3cm时,AB=3cm,AD=7cm,
∴BD===(cm);
即这个矩形的对角线的长为cm或cm;
故答案为:或.
20.如图,P为矩形ABCD内一点,PB=PC,∠BPC=90°,∠PAB=75°,若AB=11,PD=14,则PA的长为 .
解:过点A作BP的垂线,交BP于点E,
∵BP=CP,∠BPC=90°,
∴∠PBC=45°,
∵四边形ABCD是矩形,
∴△ABE是等腰直角三角形,
∵AB=11,
在△ABE中,BE=AE==11,
∵∠BAP=75°,
∴∠EAP=30°,
在Rt△AEP中,EP==,AP=2×=,
故答案为:.
三、解答题(21、22题每题7分,23、24题每题8分,25-27题每题10分,共60分)
21.如图,小明想测量学校旗杆AB的高度,他采用如下方法:先将旗杆上的绳子垂到地面,还多1米,然后将绳子下端拉直,使它的末端刚好接触地面,测得绳子下端C离旗杆底部B点5米,请你计算一下旗杆的高度.
解:设旗杆高x米,
在Rt△ABC中,由勾股定理,
(x+1)2=x2+52
解得:x=12.
答:旗杆高12米.
22.在正方形网格中,每个小正方形的边长为1.
(1)在图1中,画矩形ABCD(非正方形)使它的面积为10,要求它的顶点均在格点上.并直接写出图1中矩形ABCD的对角线长为 .
(2)在图2中,画正方形ABCD,使它的面积为13,要求它的顶点均在格点上.
解:(1)如图1中,矩形ABCD即为所求,对角线AC===.
故答案为.
(2)如图2中,正方形ABCD即为所求.
23.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,已知在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
解:过点C作CD⊥AD于点D,
∵∠EAC=60°,∠FBC=30°,
∴∠CAB=30°,∠CBD=60°.
∴在Rt△CBD中,CD=BD.
在Rt△CAD中,AD=CD=3BD=24×0.5+BD,
∴BD=6(海里).
∴CD=6(海里).
∵6>9,
∴货船继续向正东方向行驶无触礁危险.
24.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.
(1)求证:四边形GHCD为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.
解:(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中,
,
∴△GAD≌△ECD(SAS),
∴DE=DG,∠GDA=∠EDC,
∴∠GDA+∠ADF=∠EDC+∠ADF,
即∠GDF=∠ADC=90°,
∵DE⊥CH,
∴∠DFH=∠CFD=90°,
∴DG∥CH,
∵∠HCB+∠HCD=∠EDC+∠DCF=90°,
∴∠HCB=∠EDC,
在△HBC和△ECD中,
,
∴△HBC≌△ECD(ASA)
∴CH=DE,
∴DG=CH,
∵DG∥CH,
∴四边形GHCD为平行四边形;
(2)∵△HBC≌△ECD,
∴∠BHC=∠CED,
∵∠ECF+∠FEC=90°,
∴∠FEC,∠BHC与∠ECF互余;
∵AD∥BC,
∴∠ADE=∠DEC,
∴∠ADE与∠ECF互余;
∵∠DGA=∠CHB,
∴∠DGA与∠ECF互余;
∵∠DCF+∠ECF=90°,
∴∠DCF与∠ECF互余;
∴与∠ECF互余的角有:∠FEC、∠DCF、∠BHC、∠DGA、∠ADE.
25.已知一次函数y=kx+b(k≠0)的图象经过点(﹣1,﹣5),(2,1)两点.
(1)求k和b的值;
(2)一次函数y=kx+b图象与坐标轴所围成的三角形的面积.
解:(1)把点(﹣1,﹣5),(2,1)代入y=kx+b得,
解得,
所以一次函数解析式为y=2x﹣3;
(2)当y=0时,2x﹣3=0,解得x=,则一次函数与x轴的交点坐标为(,0),
当x=0时,y=﹣3,则一次函数与y轴的交点坐标为(0,﹣3),
所以一次函数图象与两坐标轴所围成的三角形面积=×3×=.
26.由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自2019年起逐月增加,据统计,该商城9月份销售自行车64辆,11月份销售了100辆;
(1)若该商城9月至11月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共100辆,已知A型车的进价为每辆500元,售价为每辆700元,B型车的进价为每辆1000元,售价为每辆1300元.假设所购进车辆全部售完,为使利润不低于26000元,该商城购进A型车不超过多少辆?
解:(1)设自行车销售的月平均增长率为x,
依题意,得:64(1+x)2=100,
解得:x1=0.25=25%,x2=﹣2.25(不合题意,舍去).
答:自行车销售的月平均增长率为25%.
(2)设该商城购进A型车m辆,则购进B型车(100﹣m)辆,
依题意,得:(700﹣500)m+(1300﹣1000)(100﹣m)≥26000,
解得:m≤40.
答:该商城购进A型车不超过40辆.
27.已知:菱形ABCD,点E在线段BC上,连接DE,点F在线段AB上,连接CF、DF,CF与DE交于点G,将菱形ABCD沿DF翻折,点A恰好落在点G上.
(1)求证:CD=CF;
(2)设∠CED=x,∠DCF=y,求y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当x=45°时,以CD为底边作等腰△CDK,顶角顶点K在菱形ABCD的内部,连接GK,若GK∥CD,CD=4时,求线段KG的长.
【解答】(1)证明:如图1中,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠AFD=∠CDF,
由翻折的性质可知,∠AFD=∠DFC,
∴∠CDF=∠DFC,
∴CD=CF.
(2)解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠ADE=∠DEC,
由翻折的性质可知,AD=DG,∠ADF=∠FDG,
∴∠FDG=∠DEC=x,
∴DG=DC,
∴∠DGC=∠DCG=y,
∵CF=CD,
∴∠CFD=(180°﹣y),
∵∠DGC=∠GFD+∠FDG,
∴y=(180°﹣y)+x,
∴y=x+60°.
(3)解:如图2中,过点K作KH⊥CD于H,过点G作GT⊥CD于T.
∵x=45°,
∴y=×45°+60°=75°,
∵DG=DC=4,
∴∠DCG=∠DGC=75°,
∴∠GDT=30°,
∵GT⊥CD,
∴∠GTD=90°,
∴GT=DG=2,DT=GT=2,
∵GK⊥CD,
∴∠KGT+∠GTH=180°,
∴∠KGT=∠GTH=90°,
∵KH⊥CD,KD=KC,
∴DH=CH=2,∠KHT=90°,
∴四边形GTHK是矩形,
∴GK=TH=DT﹣DH=2﹣2.
28.已知:如图,在平面直角坐标系中,点A的坐标为(6,0),AB=6,点P从点O出发沿线段OA向终点A运动,点P的运动速度是每秒2个单位长度,点D是线段OA的中点.
(1)求点B的坐标;
(2)设点P的运动时间为点t秒,△BDP的面积为S,求S与t的函数关系式;
(3)当点P与点D重合时,连接BP,点E在线段AB上,连接PE,当∠BPE=2∠OBP时,求点E的坐标.
解:(1)∵A(6,0),
∴OA=6,
在Rt△AOB中,∵∠AOB=90°,AB=6,OA=6,
∴OB===6,
∴B(0,6).
(2)①当0<t<3时,S=?PD?BO=?(3﹣2t)×6=9﹣6t,
当3<t≤6时,S=?DP?OB=(2t﹣3)×6=6t﹣9.
(3)如图,作PJ∥OB交AB于J,过点E作EK⊥OA于K.
∵PJ∥OB,
∴∠OBP=∠BPJ,
∵∠BPE=2∠OBP,
∴∠JPE=∠OBP,
∵EK∥PJ,
∴∠PEK=∠JPE=∠OBP,
∴tan∠PEK=tan∠OBE=,
∴=,设PK=m,则EK=2m,
∵OA=OB=6,∠AOB=90°,
∴∠EAK=45°,
∵EK⊥OA,
∴∠EKA=90°,
∴∠EAK=∠KEA=45°,
∴EK=AK=2m,
∴PA=3m=3,
∴m=1,
∴OK=4,EK=2,
∴E(4,2).
一、选择题(共10小题).
1.下列四个图象中,y不是x的函数图象的是( )
A. B.
C. D.
2.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
3.下列各点在函数y=﹣的图象上的是( )
A.(2,1) B.(﹣2,0) C.(2,0) D.(﹣2,1)
4.下列说法不能得到直角三角形的( )
A.三个角度之比为1:2:3的三角形
B.三个边长之比为3:4:5的三角形
C.三个边长之比为8:16:17的三角形
D.三个角度之比为1:1:2的三角形
5.将一根24cm的筷子,置于底面直径为15cm,高8cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是( )
A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm
6.平行四边形的两条对角线长分别是x,y,一边长为12,则x,y可能是下列各组中的( )
A.8与14 B.10与14 C.18与20 D.10与38
7.下列说法不能判断是正方形的是( )
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
8.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为40cm,钟面数字2在长方形的顶点处,则长方形的长为( )cm.
A.80 B.60 C.50 D.40
9.如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A. B. C.1 D.
10.在全民健身环城越野赛中,甲、乙两名选手各自的行程y(km)随时间t(h)变化的图象(全程)如图所示.有下列说法:①起跑后2h内,甲在乙的前面;②第1h时两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共10小题).
11.函数y=中自变量x的取值范围是 .
12.已知矩形周长为10,则矩形的长y与宽x之间的函数关系式为 .
13.在△ABC中,若a2+b2=25,a2b2=7,c=5,则最长边上的高为 .
14.三角形的三边长分别是4cm,5cm,6cm,则连结三边中点所围成的三角形的周长是 cm.
15.如图,以正方形ABCD的边AB为一边向外作等边△ABE,则∠BED= °.
16.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上点C1处,则CD的长为 .
17.如图,在△ABC中,D、E、F分别是BC、AC、AB边的中点,AH⊥BC于H,∠ACH=60°,CH=,则线段DF的长是 .
18.如图,在平行四边形ABCD中,AB=4,BC=6,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=60°,则平行四边形的面积是 .
19.矩形的一个角的平分线分一边为3cm和4cm两部分,则这个矩形的对角线的长为 cm.
20.如图,P为矩形ABCD内一点,PB=PC,∠BPC=90°,∠PAB=75°,若AB=11,PD=14,则PA的长为 .
三、解答题(21、22题每题7分,23、24题每题8分,25-27题每题10分,共60分)
21.如图,小明想测量学校旗杆AB的高度,他采用如下方法:先将旗杆上的绳子垂到地面,还多1米,然后将绳子下端拉直,使它的末端刚好接触地面,测得绳子下端C离旗杆底部B点5米,请你计算一下旗杆的高度.
22.在正方形网格中,每个小正方形的边长为1.
(1)在图1中,画矩形ABCD(非正方形)使它的面积为10,要求它的顶点均在格点上.并直接写出图1中矩形ABCD的对角线长为 .
(2)在图2中,画正方形ABCD,使它的面积为13,要求它的顶点均在格点上.
23.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,已知在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
24.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.
(1)求证:四边形GHCD为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.
25.已知一次函数y=kx+b(k≠0)的图象经过点(﹣1,﹣5),(2,1)两点.
(1)求k和b的值;
(2)一次函数y=kx+b图象与坐标轴所围成的三角形的面积.
26.由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自2019年起逐月增加,据统计,该商城9月份销售自行车64辆,11月份销售了100辆;
(1)若该商城9月至11月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共100辆,已知A型车的进价为每辆500元,售价为每辆700元,B型车的进价为每辆1000元,售价为每辆1300元.假设所购进车辆全部售完,为使利润不低于26000元,该商城购进A型车不超过多少辆?
27.已知:菱形ABCD,点E在线段BC上,连接DE,点F在线段AB上,连接CF、DF,CF与DE交于点G,将菱形ABCD沿DF翻折,点A恰好落在点G上.
(1)求证:CD=CF;
(2)设∠CED=x,∠DCF=y,求y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当x=45°时,以CD为底边作等腰△CDK,顶角顶点K在菱形ABCD的内部,连接GK,若GK∥CD,CD=4时,求线段KG的长.
28.已知:如图,在平面直角坐标系中,点A的坐标为(6,0),AB=6,点P从点O出发沿线段OA向终点A运动,点P的运动速度是每秒2个单位长度,点D是线段OA的中点.
(1)求点B的坐标;
(2)设点P的运动时间为点t秒,△BDP的面积为S,求S与t的函数关系式;
(3)当点P与点D重合时,连接BP,点E在线段AB上,连接PE,当∠BPE=2∠OBP时,求点E的坐标.
参考答案
一、选择题(共10小题).
1.下列四个图象中,y不是x的函数图象的是( )
A. B.
C. D.
解:根据函数定义,如果在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应.选项A、B、C中对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应,所以y是x的函数;而D中的y的值不具有唯一性,所以不是函数图象.
故选:D.
2.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
解:在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则v、t是变量,s是常量,
故选:C.
3.下列各点在函数y=﹣的图象上的是( )
A.(2,1) B.(﹣2,0) C.(2,0) D.(﹣2,1)
解:∵函数解析式为y=﹣,
把四个选项的坐标依次代入函数解析式,仅选项D的坐标(﹣2,1)在函数y=﹣的图象上,
∴D选项符合题意,A、B、C选项不符合题意,
故选:D.
4.下列说法不能得到直角三角形的( )
A.三个角度之比为1:2:3的三角形
B.三个边长之比为3:4:5的三角形
C.三个边长之比为8:16:17的三角形
D.三个角度之比为1:1:2的三角形
解:A、最大角=180°×=90°,故为直角三角形;
B、32+42=52,故为直角三角形;
C、82+162≠172,故不为直角三角形;
D、最大角=180°×=90°,故为直角三角形.
故选:C.
5.将一根24cm的筷子,置于底面直径为15cm,高8cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是( )
A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm
解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24﹣8=16(cm);
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=15cm,BD=8cm,
∴AB==17(cm),
所以h的取值范围是:8cm≤h≤17cm.
故选:C.
6.平行四边形的两条对角线长分别是x,y,一边长为12,则x,y可能是下列各组中的( )
A.8与14 B.10与14 C.18与20 D.10与38
解:∵四边形ABCD是平行四边形,
∴OA=OC=AC=x,OB=OD=BD=y,BC=12,
根据三角形三边关系可得:x+y>12,|y﹣x|<12,
即:x+y>24,|x﹣y|<24,
然后代入数值检验.即可得C符合要求.
故选:C.
7.下列说法不能判断是正方形的是( )
A.对角线互相垂直且相等的平行四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分的四边形
解:A.对角线互相垂直且相等的平行四边形是正方形,故A选项不符合题意;
B.对角线互相垂直的矩形是正方形,故B选项不符合题意;
C.对角线相等的菱形是正方形,故C选项不符合题意;
D.对角线互相垂直平分的四边形是菱形,菱形不一定是正方形,故D选项符合题意;
故选:D.
8.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为40cm,钟面数字2在长方形的顶点处,则长方形的长为( )cm.
A.80 B.60 C.50 D.40
解:由题意知∠AOC=2∠BOC,
∵∠AOC+∠BOC=90°,
∴∠BOC=30°,∠AOC=60°,
∴OB=BC,
∴矩形ABCD长是宽的倍,
∴长方形的长是40cm;
故选:D.
9.如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A. B. C.1 D.
解:过F作FH⊥AE于H,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE,
∴DE=BF,
∴AF=3﹣DE,
∴AE=,
∵∠FHA=∠D=∠DAF=90°,
∴∠AFH+∠HAF=∠DAE+∠FAH=90°,
∴∠DAE=∠AFH,
∴△ADE∽△AFH,
∴,
∴AE=AF,
∴=3﹣DE,
∴DE=,
故选:D.
解法二:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAH=∠AED,
∵∠ADE=∠AHF=∠DAF=90°,AD=2,FH=2,
∴AD=FH,
∴△ADE≌△FAH,
∴AF=AE,
∵AE∥CF,AF∥EC,
∴四边形AECF是平行四边形,
∵AF=AE,
∴四边形AECF是菱形,
设DE=x,则BF=x,CE=CF=3﹣x,
在Rt△BCF中,(3﹣x)2=x2+22,
∴x=.
故选:D.
10.在全民健身环城越野赛中,甲、乙两名选手各自的行程y(km)随时间t(h)变化的图象(全程)如图所示.有下列说法:①起跑后2h内,甲在乙的前面;②第1h时两人都跑了10km;③甲比乙先到达终点;④两人都跑了20km.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
解:①由横坐标看出,起跑后1小时内,甲在乙的前面,故①错误;
②由纵坐标看出,第一小时两人都跑了10千米,故②正确;
③由横坐标看出乙比甲先到达终点,故③错误;
④由纵坐标看出两人都跑了20千米,故④正确;
故选:B.
二、填空题(每小题3分,共30分)
11.函数y=中自变量x的取值范围是 x≠1 .
解:根据题意得:x﹣1≠0,
解得:x≠1.
故答案是:x≠1.
12.已知矩形周长为10,则矩形的长y与宽x之间的函数关系式为 y=5﹣x .
解:∵矩形周长=(长+宽)×2,
∴y=﹣x=5﹣x,
故答案为:y=5﹣x.
13.在△ABC中,若a2+b2=25,a2b2=7,c=5,则最长边上的高为 .
解:∵a2+b2=25,c=5,
∴a2+b2=c2,
∴△ABC是直角三角形,
∵a2b2=7,
∴ab=,
∴S△ACB==,
设最长边上的高为x,
则?x×5=,
解得:x=,
故答案为:.
14.三角形的三边长分别是4cm,5cm,6cm,则连结三边中点所围成的三角形的周长是 7.5 cm.
解:D,E,F分别是△ABC的三边的中点,
则DE=AC=2.5,DF=BC=3,EF=AB=2,
∴△DEF的周长=DE+DF+EF=2.5+3+2=7.5(cm).
故答案为:7.5.
15.如图,以正方形ABCD的边AB为一边向外作等边△ABE,则∠BED= 45 °.
解:在正方形ABCD中,AB=AD,∠BAD=90°,
在等边△ABE中,AB=AE,∠BAE=∠AEB=60°,
在△ADE中,AD=AE,∠DAE=∠BAD+∠BAE=90°+60°=150°,
所以,∠AED=(180°﹣150°)=15°,
∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°.
故答案为:45.
16.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上点C1处,则CD的长为 3 .
解:∵∠C=90°,AC=6,AB=10,
∴BC=8,
由折叠可得AC1=AC=6,
∴BC1=10﹣6=4,
设CD=x,则BD=8﹣x,
在Rt△DBC1中,42+x2=(8﹣x)2,
∴x=3.
∴CD=3,
故答案为:3.
17.如图,在△ABC中,D、E、F分别是BC、AC、AB边的中点,AH⊥BC于H,∠ACH=60°,CH=,则线段DF的长是 .
解:∵AH⊥BC,∠ACH=60°,
∴∠HAC=30°,
∴AC=2CH=,
∵D、F分别是BC、AB边的中点,
∴DF=AC=,
故答案为:.
18.如图,在平行四边形ABCD中,AB=4,BC=6,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=60°,则平行四边形的面积是 12 .
解:∵AE⊥BC于点E,AF⊥CD于点F,
∴∠AEC=90°,∠AFC=90°,
又∵∠EAF=60°,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠B=∠D=60°,
∴∠BAE=∠DAF=30°,
∵AB=4,BC=6,
∴BE=2,
∴AE==2,
∴平行四边形的面积是:2×6=12.
故答案为:12.
19.矩形的一个角的平分线分一边为3cm和4cm两部分,则这个矩形的对角线的长为 或 cm.
解:如图所示:
∵△ABCD是平行四边形,
∴AD∥BC,AC=BD,∠C=90°,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE;
当AE=4cm时,AB=4cm;AD=7cm,
∴BD===(cm);
当AE=3cm时,AB=3cm,AD=7cm,
∴BD===(cm);
即这个矩形的对角线的长为cm或cm;
故答案为:或.
20.如图,P为矩形ABCD内一点,PB=PC,∠BPC=90°,∠PAB=75°,若AB=11,PD=14,则PA的长为 .
解:过点A作BP的垂线,交BP于点E,
∵BP=CP,∠BPC=90°,
∴∠PBC=45°,
∵四边形ABCD是矩形,
∴△ABE是等腰直角三角形,
∵AB=11,
在△ABE中,BE=AE==11,
∵∠BAP=75°,
∴∠EAP=30°,
在Rt△AEP中,EP==,AP=2×=,
故答案为:.
三、解答题(21、22题每题7分,23、24题每题8分,25-27题每题10分,共60分)
21.如图,小明想测量学校旗杆AB的高度,他采用如下方法:先将旗杆上的绳子垂到地面,还多1米,然后将绳子下端拉直,使它的末端刚好接触地面,测得绳子下端C离旗杆底部B点5米,请你计算一下旗杆的高度.
解:设旗杆高x米,
在Rt△ABC中,由勾股定理,
(x+1)2=x2+52
解得:x=12.
答:旗杆高12米.
22.在正方形网格中,每个小正方形的边长为1.
(1)在图1中,画矩形ABCD(非正方形)使它的面积为10,要求它的顶点均在格点上.并直接写出图1中矩形ABCD的对角线长为 .
(2)在图2中,画正方形ABCD,使它的面积为13,要求它的顶点均在格点上.
解:(1)如图1中,矩形ABCD即为所求,对角线AC===.
故答案为.
(2)如图2中,正方形ABCD即为所求.
23.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,已知在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
解:过点C作CD⊥AD于点D,
∵∠EAC=60°,∠FBC=30°,
∴∠CAB=30°,∠CBD=60°.
∴在Rt△CBD中,CD=BD.
在Rt△CAD中,AD=CD=3BD=24×0.5+BD,
∴BD=6(海里).
∴CD=6(海里).
∵6>9,
∴货船继续向正东方向行驶无触礁危险.
24.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.
(1)求证:四边形GHCD为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.
解:(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中,
,
∴△GAD≌△ECD(SAS),
∴DE=DG,∠GDA=∠EDC,
∴∠GDA+∠ADF=∠EDC+∠ADF,
即∠GDF=∠ADC=90°,
∵DE⊥CH,
∴∠DFH=∠CFD=90°,
∴DG∥CH,
∵∠HCB+∠HCD=∠EDC+∠DCF=90°,
∴∠HCB=∠EDC,
在△HBC和△ECD中,
,
∴△HBC≌△ECD(ASA)
∴CH=DE,
∴DG=CH,
∵DG∥CH,
∴四边形GHCD为平行四边形;
(2)∵△HBC≌△ECD,
∴∠BHC=∠CED,
∵∠ECF+∠FEC=90°,
∴∠FEC,∠BHC与∠ECF互余;
∵AD∥BC,
∴∠ADE=∠DEC,
∴∠ADE与∠ECF互余;
∵∠DGA=∠CHB,
∴∠DGA与∠ECF互余;
∵∠DCF+∠ECF=90°,
∴∠DCF与∠ECF互余;
∴与∠ECF互余的角有:∠FEC、∠DCF、∠BHC、∠DGA、∠ADE.
25.已知一次函数y=kx+b(k≠0)的图象经过点(﹣1,﹣5),(2,1)两点.
(1)求k和b的值;
(2)一次函数y=kx+b图象与坐标轴所围成的三角形的面积.
解:(1)把点(﹣1,﹣5),(2,1)代入y=kx+b得,
解得,
所以一次函数解析式为y=2x﹣3;
(2)当y=0时,2x﹣3=0,解得x=,则一次函数与x轴的交点坐标为(,0),
当x=0时,y=﹣3,则一次函数与y轴的交点坐标为(0,﹣3),
所以一次函数图象与两坐标轴所围成的三角形面积=×3×=.
26.由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自2019年起逐月增加,据统计,该商城9月份销售自行车64辆,11月份销售了100辆;
(1)若该商城9月至11月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共100辆,已知A型车的进价为每辆500元,售价为每辆700元,B型车的进价为每辆1000元,售价为每辆1300元.假设所购进车辆全部售完,为使利润不低于26000元,该商城购进A型车不超过多少辆?
解:(1)设自行车销售的月平均增长率为x,
依题意,得:64(1+x)2=100,
解得:x1=0.25=25%,x2=﹣2.25(不合题意,舍去).
答:自行车销售的月平均增长率为25%.
(2)设该商城购进A型车m辆,则购进B型车(100﹣m)辆,
依题意,得:(700﹣500)m+(1300﹣1000)(100﹣m)≥26000,
解得:m≤40.
答:该商城购进A型车不超过40辆.
27.已知:菱形ABCD,点E在线段BC上,连接DE,点F在线段AB上,连接CF、DF,CF与DE交于点G,将菱形ABCD沿DF翻折,点A恰好落在点G上.
(1)求证:CD=CF;
(2)设∠CED=x,∠DCF=y,求y与x的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当x=45°时,以CD为底边作等腰△CDK,顶角顶点K在菱形ABCD的内部,连接GK,若GK∥CD,CD=4时,求线段KG的长.
【解答】(1)证明:如图1中,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠AFD=∠CDF,
由翻折的性质可知,∠AFD=∠DFC,
∴∠CDF=∠DFC,
∴CD=CF.
(2)解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠ADE=∠DEC,
由翻折的性质可知,AD=DG,∠ADF=∠FDG,
∴∠FDG=∠DEC=x,
∴DG=DC,
∴∠DGC=∠DCG=y,
∵CF=CD,
∴∠CFD=(180°﹣y),
∵∠DGC=∠GFD+∠FDG,
∴y=(180°﹣y)+x,
∴y=x+60°.
(3)解:如图2中,过点K作KH⊥CD于H,过点G作GT⊥CD于T.
∵x=45°,
∴y=×45°+60°=75°,
∵DG=DC=4,
∴∠DCG=∠DGC=75°,
∴∠GDT=30°,
∵GT⊥CD,
∴∠GTD=90°,
∴GT=DG=2,DT=GT=2,
∵GK⊥CD,
∴∠KGT+∠GTH=180°,
∴∠KGT=∠GTH=90°,
∵KH⊥CD,KD=KC,
∴DH=CH=2,∠KHT=90°,
∴四边形GTHK是矩形,
∴GK=TH=DT﹣DH=2﹣2.
28.已知:如图,在平面直角坐标系中,点A的坐标为(6,0),AB=6,点P从点O出发沿线段OA向终点A运动,点P的运动速度是每秒2个单位长度,点D是线段OA的中点.
(1)求点B的坐标;
(2)设点P的运动时间为点t秒,△BDP的面积为S,求S与t的函数关系式;
(3)当点P与点D重合时,连接BP,点E在线段AB上,连接PE,当∠BPE=2∠OBP时,求点E的坐标.
解:(1)∵A(6,0),
∴OA=6,
在Rt△AOB中,∵∠AOB=90°,AB=6,OA=6,
∴OB===6,
∴B(0,6).
(2)①当0<t<3时,S=?PD?BO=?(3﹣2t)×6=9﹣6t,
当3<t≤6时,S=?DP?OB=(2t﹣3)×6=6t﹣9.
(3)如图,作PJ∥OB交AB于J,过点E作EK⊥OA于K.
∵PJ∥OB,
∴∠OBP=∠BPJ,
∵∠BPE=2∠OBP,
∴∠JPE=∠OBP,
∵EK∥PJ,
∴∠PEK=∠JPE=∠OBP,
∴tan∠PEK=tan∠OBE=,
∴=,设PK=m,则EK=2m,
∵OA=OB=6,∠AOB=90°,
∴∠EAK=45°,
∵EK⊥OA,
∴∠EKA=90°,
∴∠EAK=∠KEA=45°,
∴EK=AK=2m,
∴PA=3m=3,
∴m=1,
∴OK=4,EK=2,
∴E(4,2).
同课章节目录
