2020-2021学年八年级数学北师大版下册 1.1.3等腰三角形(第三课时 17张)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 1.1.3等腰三角形(第三课时 17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 10:06:17 | ||
图片预览



文档简介
第一章三角形的证明
等腰三角形3
等腰三角形的两腰相等。
等腰三角形的性质
等腰三角形的两底角相等。
等腰三角形顶角的平分线、底边上的中线与底边上的高互相重合。简称“三线合一”
等腰三角形是轴对称图形,对称轴只有一条,对称轴是顶角的平分线或底边上的中线或底边上的高所在的直线。
(定义)
(性质定理)
(性质定理)
(轴对称性)
1
2
3
4
复习回顾
我们学过的等腰三角形的性质有哪些?
边:
等腰三角形的两腰相等;
角:
等腰三角形的两底角相等;简述为:等边对等角.
重要线段:
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。简述为:“三线合一”
对称性:
等腰三角形是轴对称图形,对称轴只有一条,对称轴是顶角的平分线或底边上的中线或底边上的高所在的直线。
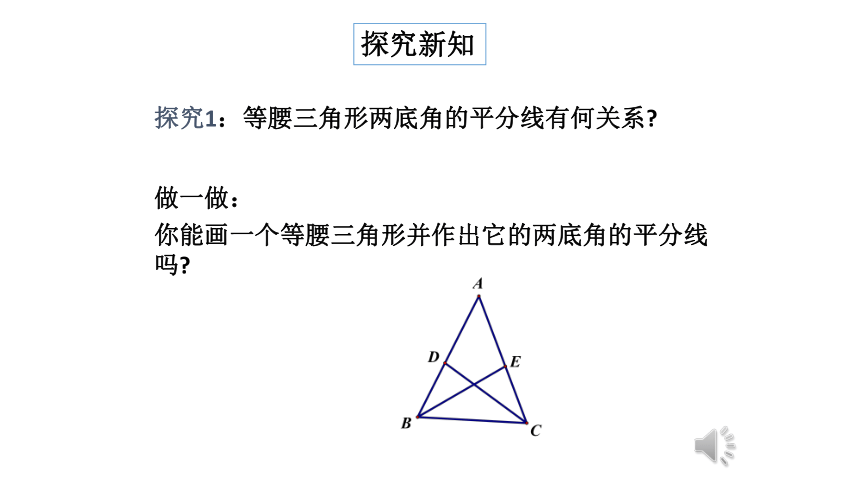
探究新知
你能画一个等腰三角形并作出它的两底角的平分线吗?
探究1:等腰三角形两底角的平分线有何关系?
做一做:
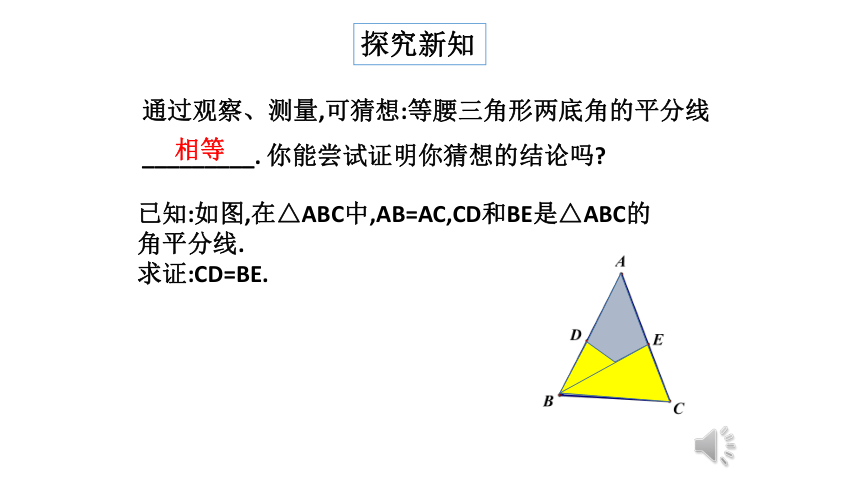
通过观察、测量,可猜想:等腰三角形两底角的平分线
_________.?你能尝试证明你猜想的结论吗?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的角平分线.
求证:CD=BE.
相等
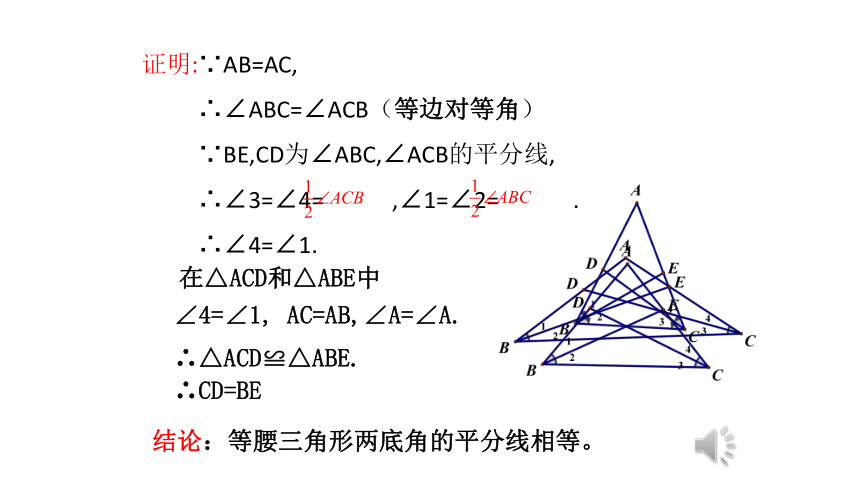
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵BE,CD为∠ABC,∠ACB的平分线,
∴∠3=∠4= ,∠1=∠2= .
∴∠4=∠1.
∠4=∠1, AC=AB,∠A=∠A.?
∴△ACD≌△ABE.
∴CD=BE?
在△ACD和△ABE中
结论:等腰三角形两底角的平分线相等。
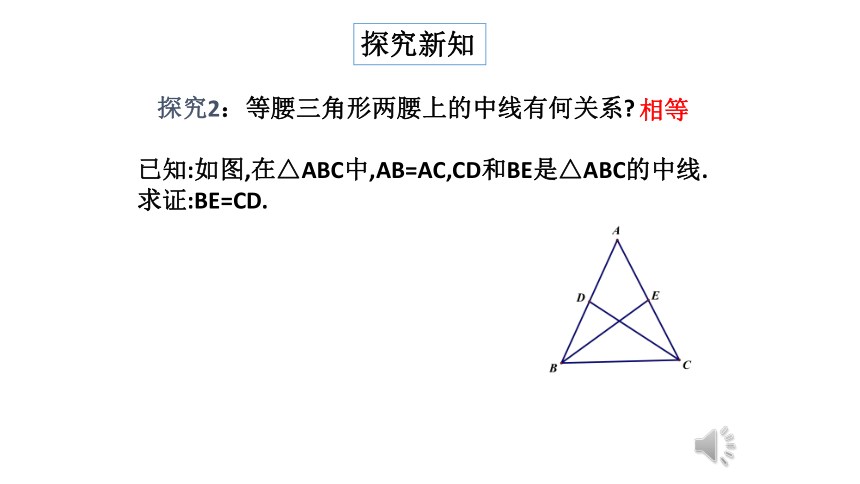
探究2:等腰三角形两腰上的中线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的中线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的中线,
∴AE= AD=
∵ AB=AC
∴AE=AD.
AB=AC,∠A=∠A,AE=AD.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的中线相等。
探究3:等腰三角形两腰上的高线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的高线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的高线,
∴
∴
∠AEB=∠ADC,∠A=∠A,AB=AC.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的高线相等。
D
E
等腰三角形重要线段的结论:
等腰三角形两个底角的平分线_________;?
等腰三角形两腰上的高_________;?
等腰三角形两腰上的中线_________.?
归纳总结
相等
相等
相等
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
选D,因为∠1和∠2都不是在同一个三角形中.
辨一辨:如图,下列推理正确吗?
请做选择:
A. 都对
B. (1)对(2)错
C. (1)错(2)对
D. 都错
(1) (2)
讲授新课
C
A
B
已知:如图,在△ABC中, ∠B=∠C,
求证:AB=AC
讲授新课
等腰三角形的判定
一
你准备如何证明:
A. 作∠A的平分线
B. 作BC上的中线
C. 作BC上的高
D. 不需要做辅助线
在△ABD与△ACD中,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
过A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
(
(
已知:如图,在△ABC中, ∠B=∠C,
求证:AB=AC
讲授新课
等腰三角形的判定
一
例1 已知:如图,AB=DC,BD=CA,BD与CA相交于点E.
求证:△AED是等腰三角形.
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边),
∴ △AED是等腰三角形.
典例精析
如何证△ABD≌△DCA
A. SSS
B. SAS
C. AAS
D. ASA
要证AE=DE你将怎么做?
A. △AEB≌△DEC
B. ∠DAC=∠ADB
讲授新课
E
2
1
A
B
C
D
72°
36°
③如果AD=4cm,则
1.已知:如图,∠A=36°,
∠DBC=36°,∠C=72°,
①∠1= , ∠2= ;
②图中有 个等腰三角形;
BC= cm;
个等腰三角形.
④如果过点D作DE∥BC,
交AB于点E,则图中有
当堂小测
求证:△OBC是等腰三角形
2.如图, 在△ABC中, AB=AC, BD和CE是△ABC的角平分线,交点为O.
当堂小测
等腰三角形3
等腰三角形的两腰相等。
等腰三角形的性质
等腰三角形的两底角相等。
等腰三角形顶角的平分线、底边上的中线与底边上的高互相重合。简称“三线合一”
等腰三角形是轴对称图形,对称轴只有一条,对称轴是顶角的平分线或底边上的中线或底边上的高所在的直线。
(定义)
(性质定理)
(性质定理)
(轴对称性)
1
2
3
4
复习回顾
我们学过的等腰三角形的性质有哪些?
边:
等腰三角形的两腰相等;
角:
等腰三角形的两底角相等;简述为:等边对等角.
重要线段:
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。简述为:“三线合一”
对称性:
等腰三角形是轴对称图形,对称轴只有一条,对称轴是顶角的平分线或底边上的中线或底边上的高所在的直线。
探究新知
你能画一个等腰三角形并作出它的两底角的平分线吗?
探究1:等腰三角形两底角的平分线有何关系?
做一做:
通过观察、测量,可猜想:等腰三角形两底角的平分线
_________.?你能尝试证明你猜想的结论吗?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的角平分线.
求证:CD=BE.
相等
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵BE,CD为∠ABC,∠ACB的平分线,
∴∠3=∠4= ,∠1=∠2= .
∴∠4=∠1.
∠4=∠1, AC=AB,∠A=∠A.?
∴△ACD≌△ABE.
∴CD=BE?
在△ACD和△ABE中
结论:等腰三角形两底角的平分线相等。
探究2:等腰三角形两腰上的中线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的中线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的中线,
∴AE= AD=
∵ AB=AC
∴AE=AD.
AB=AC,∠A=∠A,AE=AD.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的中线相等。
探究3:等腰三角形两腰上的高线有何关系?
探究新知
已知:如图,在△ABC中,AB=AC,CD和BE是△ABC的高线.
求证:BE=CD.
相等
证明: ∵BE,CD为△ABC的高线,
∴
∴
∠AEB=∠ADC,∠A=∠A,AB=AC.?
∴△ABE≌△ACD.
∴BE=CD?
在△ABE和△ACD中
结论:等腰三角形两腰上的高线相等。
D
E
等腰三角形重要线段的结论:
等腰三角形两个底角的平分线_________;?
等腰三角形两腰上的高_________;?
等腰三角形两腰上的中线_________.?
归纳总结
相等
相等
相等
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
选D,因为∠1和∠2都不是在同一个三角形中.
辨一辨:如图,下列推理正确吗?
请做选择:
A. 都对
B. (1)对(2)错
C. (1)错(2)对
D. 都错
(1) (2)
讲授新课
C
A
B
已知:如图,在△ABC中, ∠B=∠C,
求证:AB=AC
讲授新课
等腰三角形的判定
一
你准备如何证明:
A. 作∠A的平分线
B. 作BC上的中线
C. 作BC上的高
D. 不需要做辅助线
在△ABD与△ACD中,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
过A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
(
(
已知:如图,在△ABC中, ∠B=∠C,
求证:AB=AC
讲授新课
等腰三角形的判定
一
例1 已知:如图,AB=DC,BD=CA,BD与CA相交于点E.
求证:△AED是等腰三角形.
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边),
∴ △AED是等腰三角形.
典例精析
如何证△ABD≌△DCA
A. SSS
B. SAS
C. AAS
D. ASA
要证AE=DE你将怎么做?
A. △AEB≌△DEC
B. ∠DAC=∠ADB
讲授新课
E
2
1
A
B
C
D
72°
36°
③如果AD=4cm,则
1.已知:如图,∠A=36°,
∠DBC=36°,∠C=72°,
①∠1= , ∠2= ;
②图中有 个等腰三角形;
BC= cm;
个等腰三角形.
④如果过点D作DE∥BC,
交AB于点E,则图中有
当堂小测
求证:△OBC是等腰三角形
2.如图, 在△ABC中, AB=AC, BD和CE是△ABC的角平分线,交点为O.
当堂小测
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
