16.2.1 二次根式乘法 课件(共23张PPT)
文档属性
| 名称 | 16.2.1 二次根式乘法 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 18:31:40 | ||
图片预览








文档简介
(共23张PPT)
第十六章
二次根式
人教版
八年级下
16.2
二根次式
第1课时
二次根式的乘法
1.理解二次根式的乘法法则.(重点)
2.会运用二次根式的乘法法则和积的算术平方根的性
质进行简单运算.(难点)
学习目标
新知导入
一个长方形的长和宽分别是
,求这个长方形的面积.
你列出的算式是什么?这个算式应怎样计算呢?
=
?
新知讲解
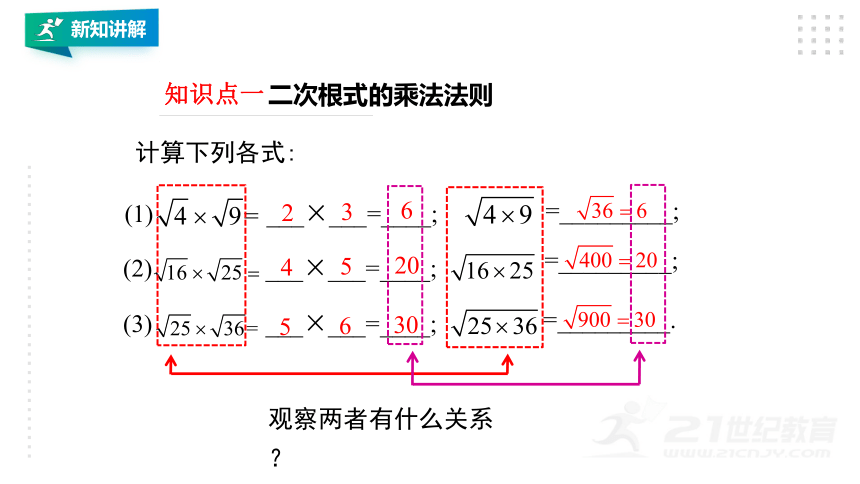
(1)
___×___=____;
=_________;
二次根式的乘法法则
计算下列各式:
(2)
___×___=____;
(3)
___×___=____;
=_________;
=_________.
2
3
6
4
5
20
5
6
30
观察两者有什么关系?
知识点一
合作探究
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考
你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
合作探究
求证:
证明:根据积的乘方法则,有
∴
就是ab算术平方根.
又∵
表示ab算术平方根,
∴
.
证一证
归纳总结
一般地,对于二次根式的乘法是
语言表述:
算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,________不变,________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
在本章中,如果没有特别说明,所有的字母都表示正数.
典例精讲
例1
计算:
解:
只需其中两个结合就可实现转化进行计算,说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘,即
.
归纳
可先用乘法结合律,再运用二次根式的乘法法则
解:原式=
=
=
解:原式=
=
=
课堂练习
(1)
(2)
(3)
(4)
当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即
.
新知讲授
把
反过来就可以进行二次根式的化简.即
知识点二
二次根式的乘法运算
(a≥0,b≥0)
例
2化简:
在本章中,如果没有特别说明,所有的字母都表示正数.
开得尽方的因式可以开方后移到根号外
(
a≥0,b≥0,c≥0
)
典例精讲
练一练
(3)
(4)
化简:
(1)
(2)
解:原式=
=
=
解:原式=
=
解:原式=
=
=
=
例5
计算:
(1)
;(2)
;
(3)
.
解:(1)
(2)
(3)
典例精讲
(4)
3.如果因式中有平方式(或平方数),应用关系式
a2
=
把这个因式(或因数)开出来,将二次根
式化简
.
1.把被开方数分解因式(或因数)
;
2.把各因式(或因数)积的算术平方根化为每个因
式(或因数)的算术平方根的积;
化简二次根式的步骤:
归纳总结
课堂练习
基础巩固
3.若直角三角形两条直角边的边长分别为
cm和
cm,那么此直角三角形的面积是
.
4.化简或计算:
解:
课堂小结
(a≥0,b≥0)
二次根式的乘法计算:
拓展:
布置作业
1.若
,则
( )
A.x≥6
B.x≥0
C.0≤x≤6
D.x为一切实数
A
2.下列运算正确的是
(
)
A.
B.
C.
D.
D
4.
比较下列两组数的大小(在横线上填“>”“<”
或“=”):
>
<
3.
计算:
https://www.21cnjy.com/help/help_extract.php
第十六章
二次根式
人教版
八年级下
16.2
二根次式
第1课时
二次根式的乘法
1.理解二次根式的乘法法则.(重点)
2.会运用二次根式的乘法法则和积的算术平方根的性
质进行简单运算.(难点)
学习目标
新知导入
一个长方形的长和宽分别是
,求这个长方形的面积.
你列出的算式是什么?这个算式应怎样计算呢?
=
?
新知讲解
(1)
___×___=____;
=_________;
二次根式的乘法法则
计算下列各式:
(2)
___×___=____;
(3)
___×___=____;
=_________;
=_________.
2
3
6
4
5
20
5
6
30
观察两者有什么关系?
知识点一
合作探究
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考
你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
合作探究
求证:
证明:根据积的乘方法则,有
∴
就是ab算术平方根.
又∵
表示ab算术平方根,
∴
.
证一证
归纳总结
一般地,对于二次根式的乘法是
语言表述:
算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,________不变,________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
在本章中,如果没有特别说明,所有的字母都表示正数.
典例精讲
例1
计算:
解:
只需其中两个结合就可实现转化进行计算,说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘,即
.
归纳
可先用乘法结合律,再运用二次根式的乘法法则
解:原式=
=
=
解:原式=
=
=
课堂练习
(1)
(2)
(3)
(4)
当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即
.
新知讲授
把
反过来就可以进行二次根式的化简.即
知识点二
二次根式的乘法运算
(a≥0,b≥0)
例
2化简:
在本章中,如果没有特别说明,所有的字母都表示正数.
开得尽方的因式可以开方后移到根号外
(
a≥0,b≥0,c≥0
)
典例精讲
练一练
(3)
(4)
化简:
(1)
(2)
解:原式=
=
=
解:原式=
=
解:原式=
=
=
=
例5
计算:
(1)
;(2)
;
(3)
.
解:(1)
(2)
(3)
典例精讲
(4)
3.如果因式中有平方式(或平方数),应用关系式
a2
=
把这个因式(或因数)开出来,将二次根
式化简
.
1.把被开方数分解因式(或因数)
;
2.把各因式(或因数)积的算术平方根化为每个因
式(或因数)的算术平方根的积;
化简二次根式的步骤:
归纳总结
课堂练习
基础巩固
3.若直角三角形两条直角边的边长分别为
cm和
cm,那么此直角三角形的面积是
.
4.化简或计算:
解:
课堂小结
(a≥0,b≥0)
二次根式的乘法计算:
拓展:
布置作业
1.若
,则
( )
A.x≥6
B.x≥0
C.0≤x≤6
D.x为一切实数
A
2.下列运算正确的是
(
)
A.
B.
C.
D.
D
4.
比较下列两组数的大小(在横线上填“>”“<”
或“=”):
>
<
3.
计算:
https://www.21cnjy.com/help/help_extract.php
