切线的性质
图片预览




文档简介
(共17张PPT)
思考:
1.什么是圆的切线 判断一条直线是圆的切线有哪些方法
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
2.前面我们已学过的切线的性质有哪些?
答:
①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。
3.切线还有什么性质?
切线的性质
观察右图:
如果直线AT是 ⊙O 的切线,A 为切点,那么 AT和半径OA是不是一定垂直?
A
T
O
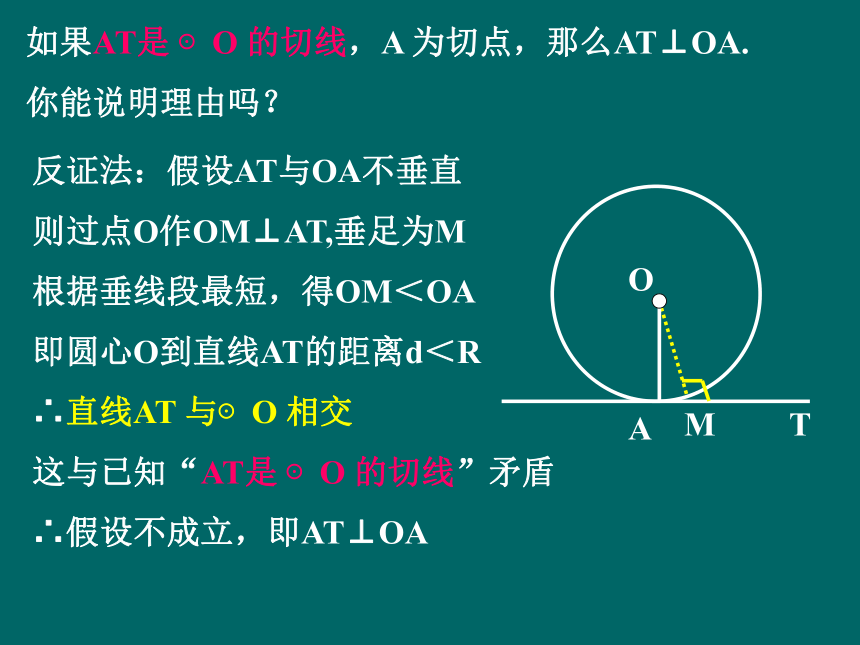
如果AT是 ⊙O 的切线,A 为切点,那么AT⊥OA.
你能说明理由吗?
A
T
O
M
反证法:假设AT与OA不垂直
则过点O作OM⊥AT,垂足为M
根据垂线段最短,得OM<OA
即圆心O到直线AT的距离d<R
∴直线AT 与⊙O 相交
这与已知“AT是 ⊙O 的切线”矛盾
∴假设不成立,即AT⊥OA
O
A
T
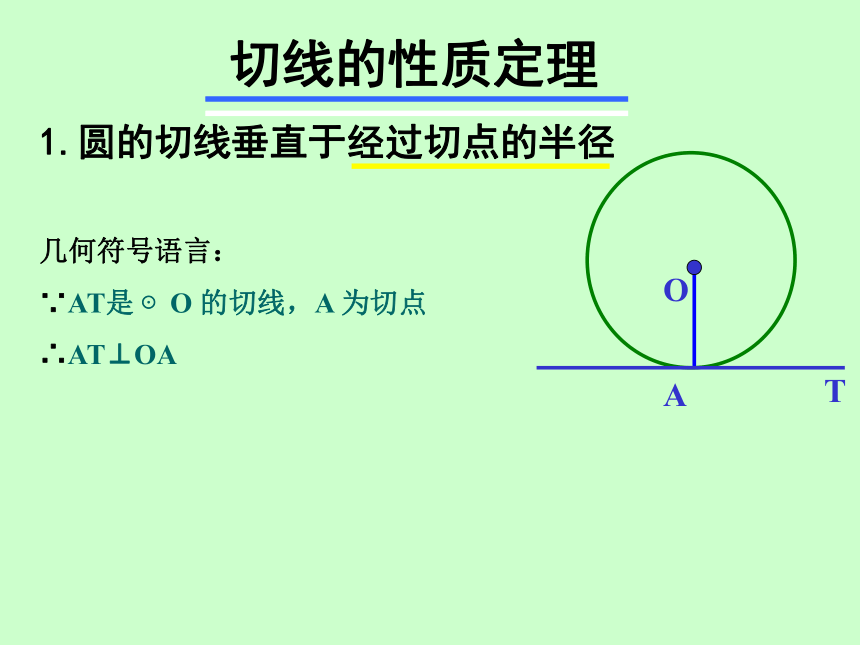
切线的性质定理
1.圆的切线垂直于经过切点的半径
几何符号语言:
∵AT是 ⊙O 的切线,A 为切点
∴AT⊥OA
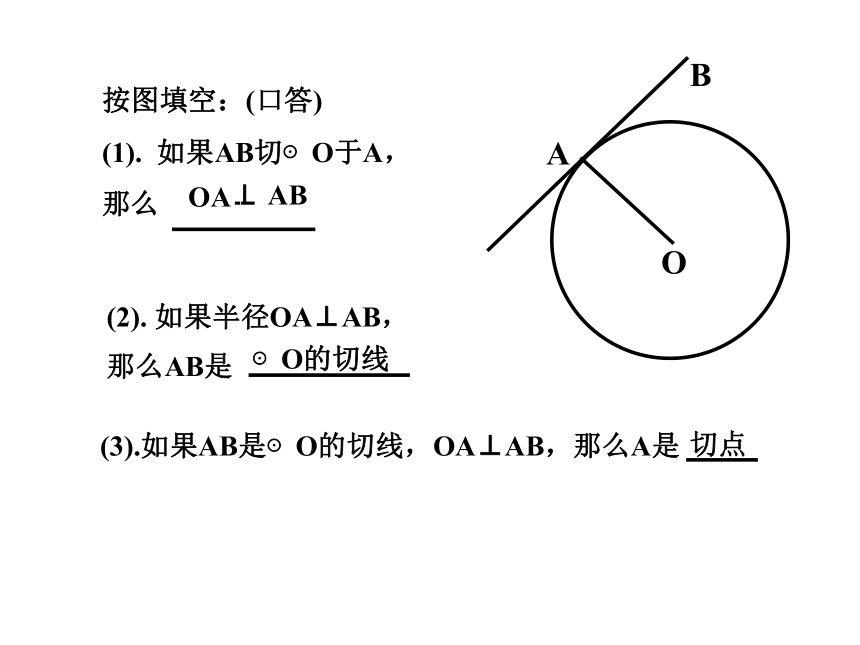
按图填空:(口答)
(1). 如果AB切⊙O于A,
那么
A
O
B
⊙O的切线
(2). 如果半径OA⊥AB,那么AB是
切点
(3).如果AB是⊙O的切线,OA⊥AB,那么A是
⊥
OA
AB.
预备练习:
1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心),∠BAC=63°,求∠ABC的度数。
2、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数。
例1、求证:经过直径的两端点的圆的切线互相平行。
C
D
O
A
B
已知:如图,AB是圆O的直径,直线AC,BD分别是过点A,B的圆O的切线。
求证 : AC BD
证明:如图,
AB 是⊙O的直径
∵AC、BD是⊙O的切线
∴AB⊥AC
AB⊥BD
∴AC∥BD
3
2
1
O
B
A
C
D
例2 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
例3:如图, PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
已知直线和圆相切时:常
连接切点与圆心。-----辅助线
若不给出图形,结果是否一样
B
A
O
P
C
C
PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
∠ACB=70°
,或 ∠ACB=110°
1
2
3
O
B
A
C
D
例4. 如图,AB为⊙O的直径, ,AD是和⊙O相切于点A的切线, ⊙O的弦BC平行于OD.
求证:DC是⊙O的切线
4
练习
如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.
C
A
B
O
证明:如图,
∴ C是AB的中点.
AC=BC
在大圆⊙O中, 根据垂径定理,得
∴OC⊥AB
连接OC, 则
∵AB是小圆的切线, C为切点
D
C
B
O
A
练习
如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.
解:∵ AB为直径
又∵BC为切线
∴∠ABC=90°
∵ △ABC为直角三角形
AD=DC
∴∠ADB=90°
∴AD=DB
∴△ABD为等腰直角三角形
∴∠ABD=45°
课堂小结
①、切线和圆有且只有一个公共点
③、圆的切线垂直于经过切点的半径
②、切线和圆心的距离等于半径
切线性质
2.能运用切线性质定理进行计算与证明。
3.掌握常见的关于切线辅助线作法
思考:
1.什么是圆的切线 判断一条直线是圆的切线有哪些方法
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
2.前面我们已学过的切线的性质有哪些?
答:
①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。
3.切线还有什么性质?
切线的性质
观察右图:
如果直线AT是 ⊙O 的切线,A 为切点,那么 AT和半径OA是不是一定垂直?
A
T
O
如果AT是 ⊙O 的切线,A 为切点,那么AT⊥OA.
你能说明理由吗?
A
T
O
M
反证法:假设AT与OA不垂直
则过点O作OM⊥AT,垂足为M
根据垂线段最短,得OM<OA
即圆心O到直线AT的距离d<R
∴直线AT 与⊙O 相交
这与已知“AT是 ⊙O 的切线”矛盾
∴假设不成立,即AT⊥OA
O
A
T
切线的性质定理
1.圆的切线垂直于经过切点的半径
几何符号语言:
∵AT是 ⊙O 的切线,A 为切点
∴AT⊥OA
按图填空:(口答)
(1). 如果AB切⊙O于A,
那么
A
O
B
⊙O的切线
(2). 如果半径OA⊥AB,那么AB是
切点
(3).如果AB是⊙O的切线,OA⊥AB,那么A是
⊥
OA
AB.
预备练习:
1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心),∠BAC=63°,求∠ABC的度数。
2、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数。
例1、求证:经过直径的两端点的圆的切线互相平行。
C
D
O
A
B
已知:如图,AB是圆O的直径,直线AC,BD分别是过点A,B的圆O的切线。
求证 : AC BD
证明:如图,
AB 是⊙O的直径
∵AC、BD是⊙O的切线
∴AB⊥AC
AB⊥BD
∴AC∥BD
3
2
1
O
B
A
C
D
例2 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
例3:如图, PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
已知直线和圆相切时:常
连接切点与圆心。-----辅助线
若不给出图形,结果是否一样
B
A
O
P
C
C
PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
∠ACB=70°
,或 ∠ACB=110°
1
2
3
O
B
A
C
D
例4. 如图,AB为⊙O的直径, ,AD是和⊙O相切于点A的切线, ⊙O的弦BC平行于OD.
求证:DC是⊙O的切线
4
练习
如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.
C
A
B
O
证明:如图,
∴ C是AB的中点.
AC=BC
在大圆⊙O中, 根据垂径定理,得
∴OC⊥AB
连接OC, 则
∵AB是小圆的切线, C为切点
D
C
B
O
A
练习
如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.
解:∵ AB为直径
又∵BC为切线
∴∠ABC=90°
∵ △ABC为直角三角形
AD=DC
∴∠ADB=90°
∴AD=DB
∴△ABD为等腰直角三角形
∴∠ABD=45°
课堂小结
①、切线和圆有且只有一个公共点
③、圆的切线垂直于经过切点的半径
②、切线和圆心的距离等于半径
切线性质
2.能运用切线性质定理进行计算与证明。
3.掌握常见的关于切线辅助线作法
