六年级下册数学课件-第四单元 4.反比例 北师大版(共25张PPT)
文档属性
| 名称 | 六年级下册数学课件-第四单元 4.反比例 北师大版(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 15:01:40 | ||
图片预览







文档简介
反 比 例
北师大版六年级下册
什么是正比例?成正比例的量有什么特点?
两种相关联的量,一种量变化,另一种量也随着变化,并且这两种量中相对应的两个数的比值(也就是商)一定。像这样的两种量我们就说它们成正比例。
还记正比例吗?回忆一下,然后回答左边的问题。
yx=k(一定)
?
下面三个问题中,哪两种量成正比例?为什么?
(1)速度一定,路程与时间。
(2)时间一定,路程与速度。
(3)路程一定,速度与时间。
速度一定,路程与时间成正比例。因为路程与时间是相关联的量,路程÷时间=速度,所以速度一定,路程与时间成正比例。
时间一定,路程与速度成正比例。因为路程与速度是相关联的量,路程÷速度=时间,所以时间一定,路程与速度成正比例。
路程一定,速度与时间不成正比例。因为路程=速度×时间,路程一定,速度与时间的乘积一定,而不是比值一定,所以不成正比例。
用x , y表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
借助表格寻找共同规律
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
24
12
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
11
10
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
24
12
表1
8
6
6
4
8
3
12
2
24
1
(1)在表1中,有哪几个变量?
长方形的相邻两边边长(即长和宽)这两个变量。
(2)这两个变量之间有什么关系呢?请完成表1。
长方形的一条边长增加,相邻的边长减少。
表2
9
8
5
7
6
6
7
5
8
4
(1)在表2中,有哪几个变量?
长方形的相邻两边边长(即长和宽)这两个变量。
(2)这两个变量之间有什么关系呢?请完成表2。
长方形的一条边长增加,相邻的边长减少。
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
11
10
通过表1和表2我们发现,问题中的两个长方形的相邻两边边长有着相同的变化规律。
有什么相同的规律呢?
长方形一条边的长随着邻边长的增加而减少。
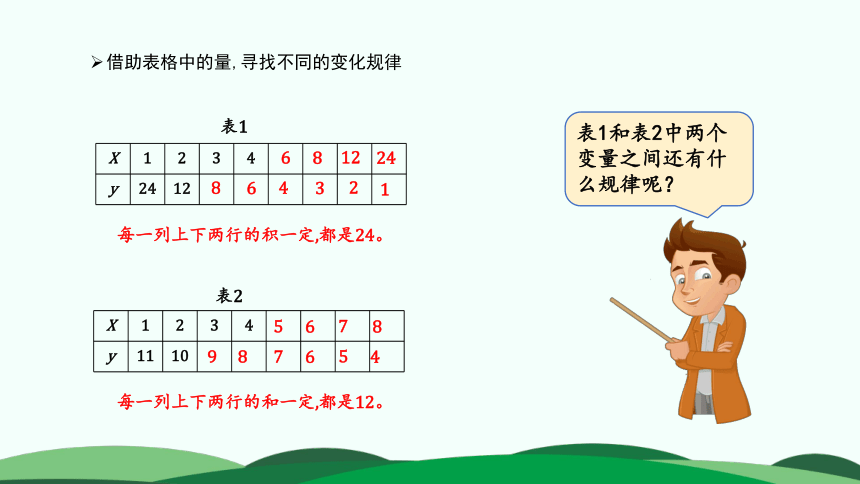
每一列上下两行的积一定,都是24。
每一列上下两行的和一定,都是12。
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
24
12
表1
8
6
6
4
8
3
12
2
24
1
表2
9
8
5
7
6
6
7
5
8
4
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
11
10
借助表格中的量,寻找不同的变化规律
表1和表2中两个变量之间还有什么规律呢?
王叔叔要去游长城,不同的交通工具的速度和行驶所需时间如下。你从表中发现了什么?
{5940675A-B579-460E-94D1-54222C63F5DA}
自行车
大巴车
小轿车
速度(千米/时)
10
60
80
时间/时
12
2
1.5
探究反比例的意义
时间是随着速度的变化而变化的。
10×12=60×2=80×
1.5,积都是120。
速度和时间这两个量,速度变化,所用的时间也随着变化,而且速度与时间的积(也就是路程)一定,我们就说速度和时间成反比例。
速度×时间=路程(一定)
通过上面的观察分析你们发现了什么?你们能写出关系式吗?
两种相关联的量,其中一种量在变化,另一种量也随着变化,并且这两种量中相对应的两个数的积是一定的。像这样两种相关联的量就成反比例。
x y =k(一定)
具有刚才那种关联关系的量我们又叫什么呢?
买苹果的总钱数一定,苹果的单价与数量成反比例吗?你是怎么想的?与同伴交流。
买苹果的总钱数一定时,苹果的单价与数量成反比例。苹果的单价增加,数量就减少;苹果的单价减少,数量就增加。单价与数量的积是一定的。
分析两个变量是否成反比例
奇思读一本书,已读的页数与剩下的页数的情况如下:
已读的页数
1
2
3
4
…
剩下的页数
79
78
77
…
(1)请同学们独立把表格填写完整。
76
5
75
领悟生活中变量之间关系的多样性
(2)试判断已读的页数与剩下的页数成反比例吗? 为什么?
不成反比例
生活中成反比例的例子还有很多,请同学们分别找一找,再与同伴交流。
生活中的反比例
如:长方形面积一定时,长与宽成反比例。路程一定时,速度和时间成反比例。
1.
{5940675A-B579-460E-94D1-54222C63F5DA}平均每天看的页数
10
15
20
30
40
看完全书所需天数
12
⑴把上表补充完整。
8
6
4
3
⑵说一说看完全书所需天数与平均每天看的页数的变化关系。
看完全书所需天数随平均每天看的页数的增加而减少。
⑶平均每天看的页数与看完全书所需天数是不是成反比例?说明理由。
因为平均每天看的页数与看完全书所需天数的乘积一定(总页数为120页),所以它们成反比例。
2.电脑兴趣小组练习打同一份稿件,下表记录的是每人打字所用的时间。
{5940675A-B579-460E-94D1-54222C63F5DA}
小敏
小峰
小英
小强
打字所用的时间/分
30
40
60
80
速度/(字/分)
80
请把上表补充完整,再回答下列问题。
60
40
30
⑴不同的人在打同一份稿件的过程中,哪个量没有变?
不同的人在打同一份稿件的过程中,总字数没有变。
⑵打字的速度和所用的时间有什么关系?
打字的速度随打字所用的时间的变化而变化,并且它们的乘积一定(总字数为2400个),所以它们成反比例。
2.电脑兴趣小组练习打同一份稿件,下表记录的是每人打字所用的时间。
{5940675A-B579-460E-94D1-54222C63F5DA}
小敏
小峰
小英
小强
打字所用的时间/分
30
40
60
80
速度/(字/分)
80
60
40
30
⑶李老师打这份稿件用了24分,你知道她平均每分打多少字吗?
平均每分钟打100个字。
2.电脑兴趣小组练习打同一份稿件,下表记录的是每人打字所用的时间。
{5940675A-B579-460E-94D1-54222C63F5DA}
小敏
小峰
小英
小强
打字所用的时间/分
30
40
60
80
速度/(字/分)
80
60
40
30
3.如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转动的总齿数是相同的。尝试回答下面的问题。
⑴大齿轮和小齿轮在同一时间内转动时,哪个齿轮转得更快?哪个齿轮转的圈数多?
小齿轮
小齿轮
⑵转过的总齿数一定时,每个齿轮的齿数和转过的圈数是什么关系?
成反比例关系
⑶大齿轮有40个齿,小齿轮有24个齿。如果大齿轮每分转
90圈,小齿轮每分转多少圈?
40×90÷24=150(圈)
答:小齿轮每分转150圈。
4.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
{5940675A-B579-460E-94D1-54222C63F5DA}每块地砖的面积/m2
0.2
0.3
0.4
0.6
0.8
…
所需地砖的数量/块
600
400
300
200
150
…
(1)每块地砖的面积和所需地砖的数量有什么关系?
每块地砖的面积和所需地砖的数量成反比例。
(2)如果每块地砖的面积是0.5m?,铺这一地面需要多少块地砖?
0.2×600÷0.5=240(块)
答:需要240块地砖。
(3)铺这一地面用了500块地砖,所用的地砖每块面积是多大?
0.2×600÷500=0.24(m?)
答:所用的地砖每块面积是0.24m?。
4.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
{5940675A-B579-460E-94D1-54222C63F5DA}每块地砖的面积/m2
0.2
0.3
0.4
0.6
0.8
…
所需地砖的数量/块
600
400
300
200
150
…
5.某大型酒店为迎接宾客,重新为酒店大厅铺地砖。设计了以下几种铺设方案并绘制出了图象。
每块面积/m?
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
500
1000
1500
2000
2500
3000
需要的块数/块
A
B
(1)点A,B 分别表示什么意义?
点A表示:用每块面积是0.3 m2的地砖,需铺2000块;
点B表示:用每块面积是0.6 m2的地砖,需铺1000块。
(2)从图象上估计一下,如果每块地砖的面积是0.8 m2,需要多少块地砖?
750块
如果速度和时间相对应的两个数的乘积(也就是路程)一定,我们就说速度和时间成反比例。
判断两种量是否成反比例,首先要判断这两种量是不是相关联的量,再运用数量关系式进行判断,看这两种量的积是否一定,最后得出结论。
北师大版六年级下册
什么是正比例?成正比例的量有什么特点?
两种相关联的量,一种量变化,另一种量也随着变化,并且这两种量中相对应的两个数的比值(也就是商)一定。像这样的两种量我们就说它们成正比例。
还记正比例吗?回忆一下,然后回答左边的问题。
yx=k(一定)
?
下面三个问题中,哪两种量成正比例?为什么?
(1)速度一定,路程与时间。
(2)时间一定,路程与速度。
(3)路程一定,速度与时间。
速度一定,路程与时间成正比例。因为路程与时间是相关联的量,路程÷时间=速度,所以速度一定,路程与时间成正比例。
时间一定,路程与速度成正比例。因为路程与速度是相关联的量,路程÷速度=时间,所以时间一定,路程与速度成正比例。
路程一定,速度与时间不成正比例。因为路程=速度×时间,路程一定,速度与时间的乘积一定,而不是比值一定,所以不成正比例。
用x , y表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
借助表格寻找共同规律
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
24
12
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
11
10
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
24
12
表1
8
6
6
4
8
3
12
2
24
1
(1)在表1中,有哪几个变量?
长方形的相邻两边边长(即长和宽)这两个变量。
(2)这两个变量之间有什么关系呢?请完成表1。
长方形的一条边长增加,相邻的边长减少。
表2
9
8
5
7
6
6
7
5
8
4
(1)在表2中,有哪几个变量?
长方形的相邻两边边长(即长和宽)这两个变量。
(2)这两个变量之间有什么关系呢?请完成表2。
长方形的一条边长增加,相邻的边长减少。
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
11
10
通过表1和表2我们发现,问题中的两个长方形的相邻两边边长有着相同的变化规律。
有什么相同的规律呢?
长方形一条边的长随着邻边长的增加而减少。
每一列上下两行的积一定,都是24。
每一列上下两行的和一定,都是12。
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
24
12
表1
8
6
6
4
8
3
12
2
24
1
表2
9
8
5
7
6
6
7
5
8
4
{5940675A-B579-460E-94D1-54222C63F5DA}X
1
2
3
4
y
11
10
借助表格中的量,寻找不同的变化规律
表1和表2中两个变量之间还有什么规律呢?
王叔叔要去游长城,不同的交通工具的速度和行驶所需时间如下。你从表中发现了什么?
{5940675A-B579-460E-94D1-54222C63F5DA}
自行车
大巴车
小轿车
速度(千米/时)
10
60
80
时间/时
12
2
1.5
探究反比例的意义
时间是随着速度的变化而变化的。
10×12=60×2=80×
1.5,积都是120。
速度和时间这两个量,速度变化,所用的时间也随着变化,而且速度与时间的积(也就是路程)一定,我们就说速度和时间成反比例。
速度×时间=路程(一定)
通过上面的观察分析你们发现了什么?你们能写出关系式吗?
两种相关联的量,其中一种量在变化,另一种量也随着变化,并且这两种量中相对应的两个数的积是一定的。像这样两种相关联的量就成反比例。
x y =k(一定)
具有刚才那种关联关系的量我们又叫什么呢?
买苹果的总钱数一定,苹果的单价与数量成反比例吗?你是怎么想的?与同伴交流。
买苹果的总钱数一定时,苹果的单价与数量成反比例。苹果的单价增加,数量就减少;苹果的单价减少,数量就增加。单价与数量的积是一定的。
分析两个变量是否成反比例
奇思读一本书,已读的页数与剩下的页数的情况如下:
已读的页数
1
2
3
4
…
剩下的页数
79
78
77
…
(1)请同学们独立把表格填写完整。
76
5
75
领悟生活中变量之间关系的多样性
(2)试判断已读的页数与剩下的页数成反比例吗? 为什么?
不成反比例
生活中成反比例的例子还有很多,请同学们分别找一找,再与同伴交流。
生活中的反比例
如:长方形面积一定时,长与宽成反比例。路程一定时,速度和时间成反比例。
1.
{5940675A-B579-460E-94D1-54222C63F5DA}平均每天看的页数
10
15
20
30
40
看完全书所需天数
12
⑴把上表补充完整。
8
6
4
3
⑵说一说看完全书所需天数与平均每天看的页数的变化关系。
看完全书所需天数随平均每天看的页数的增加而减少。
⑶平均每天看的页数与看完全书所需天数是不是成反比例?说明理由。
因为平均每天看的页数与看完全书所需天数的乘积一定(总页数为120页),所以它们成反比例。
2.电脑兴趣小组练习打同一份稿件,下表记录的是每人打字所用的时间。
{5940675A-B579-460E-94D1-54222C63F5DA}
小敏
小峰
小英
小强
打字所用的时间/分
30
40
60
80
速度/(字/分)
80
请把上表补充完整,再回答下列问题。
60
40
30
⑴不同的人在打同一份稿件的过程中,哪个量没有变?
不同的人在打同一份稿件的过程中,总字数没有变。
⑵打字的速度和所用的时间有什么关系?
打字的速度随打字所用的时间的变化而变化,并且它们的乘积一定(总字数为2400个),所以它们成反比例。
2.电脑兴趣小组练习打同一份稿件,下表记录的是每人打字所用的时间。
{5940675A-B579-460E-94D1-54222C63F5DA}
小敏
小峰
小英
小强
打字所用的时间/分
30
40
60
80
速度/(字/分)
80
60
40
30
⑶李老师打这份稿件用了24分,你知道她平均每分打多少字吗?
平均每分钟打100个字。
2.电脑兴趣小组练习打同一份稿件,下表记录的是每人打字所用的时间。
{5940675A-B579-460E-94D1-54222C63F5DA}
小敏
小峰
小英
小强
打字所用的时间/分
30
40
60
80
速度/(字/分)
80
60
40
30
3.如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转动的总齿数是相同的。尝试回答下面的问题。
⑴大齿轮和小齿轮在同一时间内转动时,哪个齿轮转得更快?哪个齿轮转的圈数多?
小齿轮
小齿轮
⑵转过的总齿数一定时,每个齿轮的齿数和转过的圈数是什么关系?
成反比例关系
⑶大齿轮有40个齿,小齿轮有24个齿。如果大齿轮每分转
90圈,小齿轮每分转多少圈?
40×90÷24=150(圈)
答:小齿轮每分转150圈。
4.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
{5940675A-B579-460E-94D1-54222C63F5DA}每块地砖的面积/m2
0.2
0.3
0.4
0.6
0.8
…
所需地砖的数量/块
600
400
300
200
150
…
(1)每块地砖的面积和所需地砖的数量有什么关系?
每块地砖的面积和所需地砖的数量成反比例。
(2)如果每块地砖的面积是0.5m?,铺这一地面需要多少块地砖?
0.2×600÷0.5=240(块)
答:需要240块地砖。
(3)铺这一地面用了500块地砖,所用的地砖每块面积是多大?
0.2×600÷500=0.24(m?)
答:所用的地砖每块面积是0.24m?。
4.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
{5940675A-B579-460E-94D1-54222C63F5DA}每块地砖的面积/m2
0.2
0.3
0.4
0.6
0.8
…
所需地砖的数量/块
600
400
300
200
150
…
5.某大型酒店为迎接宾客,重新为酒店大厅铺地砖。设计了以下几种铺设方案并绘制出了图象。
每块面积/m?
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
500
1000
1500
2000
2500
3000
需要的块数/块
A
B
(1)点A,B 分别表示什么意义?
点A表示:用每块面积是0.3 m2的地砖,需铺2000块;
点B表示:用每块面积是0.6 m2的地砖,需铺1000块。
(2)从图象上估计一下,如果每块地砖的面积是0.8 m2,需要多少块地砖?
750块
如果速度和时间相对应的两个数的乘积(也就是路程)一定,我们就说速度和时间成反比例。
判断两种量是否成反比例,首先要判断这两种量是不是相关联的量,再运用数量关系式进行判断,看这两种量的积是否一定,最后得出结论。
