六年级下册数学课件-数学好玩-2.神奇的莫比乌斯带 北师大版(共20张PPT)
文档属性
| 名称 | 六年级下册数学课件-数学好玩-2.神奇的莫比乌斯带 北师大版(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 15:02:36 | ||
图片预览








文档简介
神奇的莫比乌斯带
北师大版六年级下册
发挥你们的聪明才智想想该怎么解决这个有趣的问题吧!
下面是一个纸环,如果不穿过这个纸环的面,你
有办法用铅笔一次性画过纸环的内侧和外侧面吗?
一个纸环的内侧有一点面包屑,外面有一只蚂蚁。如果不让蚂蚁爬过纸环的边缘,它能吃到面包屑吗?
面包屑在里面,蚂蚁在外面,吃不到吧。
现在请同学们拿出课前你们准备好的纸条,然后说一说纸条有什么特点。
做一做——神奇的带子
长方形纸条有4条边、2个面。
你们能把它变成两条边吗?请同学们动手试一试。
你能把这2个面变成1个面吗?
制作方法:
先围成一个普通的纸环,然后将一端翻转180°,再用胶带粘牢。
做一做——神奇的带子
现在蚂蚁能吃到面包屑了吗?想一想,怎样验证呢?
做一做——神奇的带子
操作提示:
在带子上点上两个点,其中一个代表面包屑,一个代表蚂蚁。
标记好面包屑和蚂蚁,认真观察后你有什么发现?
不管面包屑标在什么地方,小蚂蚁都能吃到。
做一做——神奇的带子
操作提示:
分别在“神奇的纸环”上各取一点。从这点开始涂色,
不能翻过边缘一直涂下去
这样一个纸环真的只有一条边、一个面吗?我们一起来检验吧!
“神奇的纸环”上全涂了颜色,又回到了起点,说明只有一个面。
你们有什么发现?
你们知道这样的一个纸环叫什么名字吗?
它是德国数学家莫比乌斯在1858年偶然间发现的,所以就以他的名字命名为“莫比乌斯带”,也有人叫它“莫比乌斯圈”,还有人管它叫“怪圈”。
做一做——神奇的带子
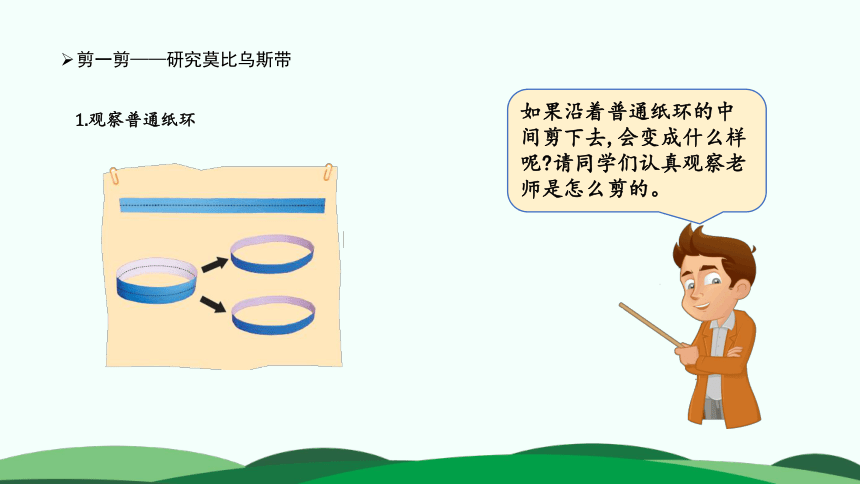
1.观察普通纸环
剪一剪——研究莫比乌斯带
如果沿着普通纸环的中间剪下去,会变成什么样呢?请同学们认真观察老师是怎么剪的。
2.观察“神奇的纸环”
剪一剪——研究莫比乌斯带
莫比乌斯带我们也用剪刀沿中间剪开,同学们猜一猜会变成什么样子?
操作提示:
不把纸环剪断,先看老师演示,然后再动手剪,大家剪的时候一定要注意安全!
在这个纸环中间画一条线,沿着中间这条线把这个纸环剪开。
2.观察“神奇的纸环”
剪一剪——研究莫比乌斯带
剪完的同学举起来给大家看一看,发生了什么神奇的事情?
3.继续神奇
剪一剪——研究莫比乌斯带
大家还想不想继续感受这个纸环的神奇?如果我们要沿着三等分线剪,猜一猜:要剪几次?剪的结果会是怎样呢?说说自己的想法。
课后同学们去实践一下,看看是不是你们猜想的结果。
说一说——莫比乌斯带的应用
如此神奇的“莫比乌斯带”在生活中有哪些应用呢?一起来欣赏几张图片吧!
过山车
(有些过山车的轨道采用
的就是莫比乌斯带原理)
说一说——莫比乌斯带的应用
莫比乌斯爬梯
说一说——莫比乌斯带的应用
哈萨克斯坦新国家图书馆
说一说——莫比乌斯带的应用
克莱因瓶是由德国数学家菲利克斯·克莱因提出的。
克莱因瓶的结构非常简单,一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。和我们平时用来喝水的杯子不一样,这个物体没有“边”,它的表面不会终结。它也不类似于气球 ,一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面(所以说它没有内外部之分)。
说一说——莫比乌斯带的应用
三叶扭结
一个长条扭一扭,两条短边手牵手,
变出莫比乌斯带,单侧曲面把路开。
课后查阅资料继续了解有关神奇的“莫比乌斯带”的应用实例。
北师大版六年级下册
发挥你们的聪明才智想想该怎么解决这个有趣的问题吧!
下面是一个纸环,如果不穿过这个纸环的面,你
有办法用铅笔一次性画过纸环的内侧和外侧面吗?
一个纸环的内侧有一点面包屑,外面有一只蚂蚁。如果不让蚂蚁爬过纸环的边缘,它能吃到面包屑吗?
面包屑在里面,蚂蚁在外面,吃不到吧。
现在请同学们拿出课前你们准备好的纸条,然后说一说纸条有什么特点。
做一做——神奇的带子
长方形纸条有4条边、2个面。
你们能把它变成两条边吗?请同学们动手试一试。
你能把这2个面变成1个面吗?
制作方法:
先围成一个普通的纸环,然后将一端翻转180°,再用胶带粘牢。
做一做——神奇的带子
现在蚂蚁能吃到面包屑了吗?想一想,怎样验证呢?
做一做——神奇的带子
操作提示:
在带子上点上两个点,其中一个代表面包屑,一个代表蚂蚁。
标记好面包屑和蚂蚁,认真观察后你有什么发现?
不管面包屑标在什么地方,小蚂蚁都能吃到。
做一做——神奇的带子
操作提示:
分别在“神奇的纸环”上各取一点。从这点开始涂色,
不能翻过边缘一直涂下去
这样一个纸环真的只有一条边、一个面吗?我们一起来检验吧!
“神奇的纸环”上全涂了颜色,又回到了起点,说明只有一个面。
你们有什么发现?
你们知道这样的一个纸环叫什么名字吗?
它是德国数学家莫比乌斯在1858年偶然间发现的,所以就以他的名字命名为“莫比乌斯带”,也有人叫它“莫比乌斯圈”,还有人管它叫“怪圈”。
做一做——神奇的带子
1.观察普通纸环
剪一剪——研究莫比乌斯带
如果沿着普通纸环的中间剪下去,会变成什么样呢?请同学们认真观察老师是怎么剪的。
2.观察“神奇的纸环”
剪一剪——研究莫比乌斯带
莫比乌斯带我们也用剪刀沿中间剪开,同学们猜一猜会变成什么样子?
操作提示:
不把纸环剪断,先看老师演示,然后再动手剪,大家剪的时候一定要注意安全!
在这个纸环中间画一条线,沿着中间这条线把这个纸环剪开。
2.观察“神奇的纸环”
剪一剪——研究莫比乌斯带
剪完的同学举起来给大家看一看,发生了什么神奇的事情?
3.继续神奇
剪一剪——研究莫比乌斯带
大家还想不想继续感受这个纸环的神奇?如果我们要沿着三等分线剪,猜一猜:要剪几次?剪的结果会是怎样呢?说说自己的想法。
课后同学们去实践一下,看看是不是你们猜想的结果。
说一说——莫比乌斯带的应用
如此神奇的“莫比乌斯带”在生活中有哪些应用呢?一起来欣赏几张图片吧!
过山车
(有些过山车的轨道采用
的就是莫比乌斯带原理)
说一说——莫比乌斯带的应用
莫比乌斯爬梯
说一说——莫比乌斯带的应用
哈萨克斯坦新国家图书馆
说一说——莫比乌斯带的应用
克莱因瓶是由德国数学家菲利克斯·克莱因提出的。
克莱因瓶的结构非常简单,一个瓶子底部有一个洞,现在延长瓶子的颈部,并且扭曲地进入瓶子内部,然后和底部的洞相连接。和我们平时用来喝水的杯子不一样,这个物体没有“边”,它的表面不会终结。它也不类似于气球 ,一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面(所以说它没有内外部之分)。
说一说——莫比乌斯带的应用
三叶扭结
一个长条扭一扭,两条短边手牵手,
变出莫比乌斯带,单侧曲面把路开。
课后查阅资料继续了解有关神奇的“莫比乌斯带”的应用实例。
