直线与圆的位置关系复习课件
图片预览






文档简介
(共16张PPT)
a(地平线)
(1)
(3)
(2)
[复习导引]
《直线与圆的位置关系》
复习课
[课题展示]
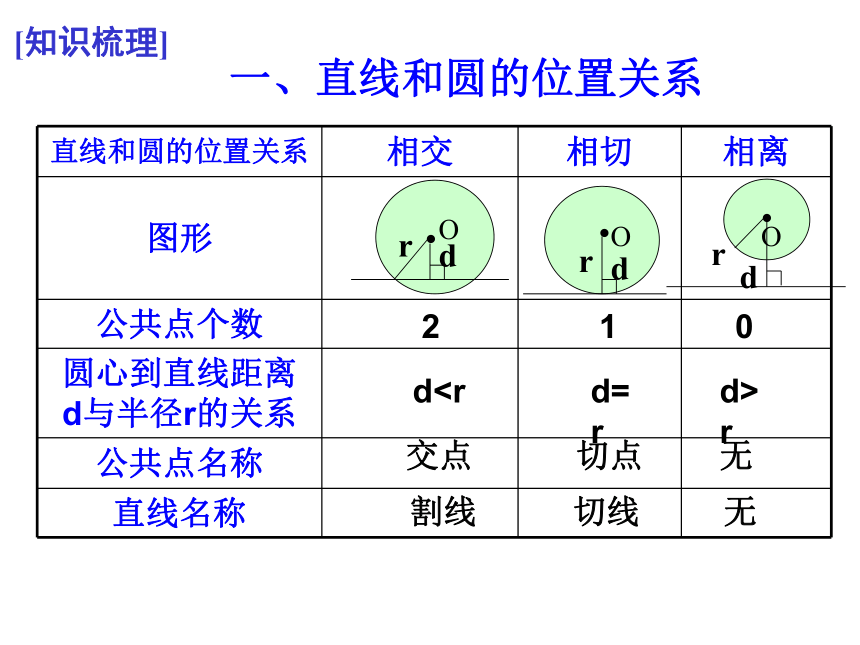
一、直线和圆的位置关系
直线和圆的位置关系 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
dd=r
d>r
交点
切点
无
割线
切线
无
O
d
r
O
l
d
r
O
d
r
[知识梳理]
1、⊙O的半径为r ,圆心O到直线a 的距离为d
(1)r=4,d=3,则直线a与⊙O
(2)r=4,d=4,则直线a与⊙O
(3)若直线a与⊙O相离,r=4,则d的取值范围为
相交
相切
2、如图,Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
⊙C的半径为2.4cm,则⊙C与线段AB的位置关系为
C
B
A
d>4
相切
D
[小试牛刀]
C
B
A
变一变:如图,Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,⊙C与线段AB只有一个公共点,则⊙C半径r的取值范围是
[初露锋芒]
二、切线的判定方法
③切线的判定定理:
②比较法(d=r):
圆心的距离到直线等于圆的半径。
①定义法: 直线与圆只有一个公共点。
经过半径外端并且垂直于这条半径的直线是圆的切线。
[方法归类]
1、如图,线段AB经过圆心O,与⊙O交于点A、C,∠BAD=∠B=30°,边BD交圆于点D。那么BD是⊙O的切线吗?为什么?
O
A
B
C
D
答:BD是⊙O的切线
理由:连结OD,
∵∠BAD=∠B=30°
∴∠ADB=120°
又∵OA=OD
∴∠ODA=30°
∴∠ODB=90°
∴BD是⊙O的切线
[知识应用]
A
B
D
O
C
2、△ABC中,AB=AC,AO是底边BC上的中线,以O为圆心的圆与AB边相切,切点为D。
求证:⊙O也与AC边相切。
E
证明:过O作OE⊥AC于E。
∵AB=AC
又∵AO是BC边上的中线
∴AO是∠BAC的平分线
∵AB与⊙O相切
∴ OD⊥AB,
又∵ OE⊥AC
∴OE=OD
∴OE是⊙O的切线
[知识应用]
3、如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E。
由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
D
E
C
O
B
A
[拓展思维]
三、切线的性质
1、经过切点的半径垂直与圆的切线;
2、经过切点垂直于切线的直线必经过圆心。
A
B
O
T
[知识回放]
1、如图,A、B两点在⊙O上,AC是⊙O的切线,∠B=65°,则∠BAC=
2、已知,PA为⊙O的切线,A为切点,OP交⊙O于点B,PB=2,PA =4。则⊙O的半径r=
C
A
B
O
[练习巩固]
[综合强化]
3、已知:如图,CD切⊙O于D,割线CBA经过点O,
DE⊥AB,垂足为E。求证:∠1=∠2。
2
1
O
A
C
D
E
B
[盘点收获]
这一节课我们复习了哪些内容?
你掌握了哪些添辅助线的方法?
你最感兴趣的是哪些?
本课中涉及的数学思想有哪些?
1.:如图,正三角形ABC的边长为6 厘米,⊙O的半径为r厘米,当圆心O从点A出发,沿着线路AB一BC一CA运动,回到点A时,⊙O随着点O的运动而移动.在⊙O移动过程中,从切点的个数来考虑,相切有几种不同的情况?写出不同情况下,r的取值范围及相应的切点个数.
A
B
C
2.如图:菱形ABCD的边长为5cm,∠B=60°当以A为圆心的圆与BC相切时,半径是 ,此时⊙A与CD的位置关系是 。
3.如图,一热带风暴中心O距A岛为2千米,风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行,问∠BAO的度数是多少时船就会进入风暴影响圈?
4.如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30° ,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径.
挑战自我!
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动。设运动时间为t(s)。
(1)求PQ的长;
(2)当t为何值时,直线AB与⊙O相切?
[激荡思维]
.
B
P
A
Q
M
N
.
O
引申:当0.5﹤t﹤3.5时,你能否求出直线 AB被⊙O截得的弦长关于时间t的表达式?
a(地平线)
(1)
(3)
(2)
[复习导引]
《直线与圆的位置关系》
复习课
[课题展示]
一、直线和圆的位置关系
直线和圆的位置关系 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
d
d>r
交点
切点
无
割线
切线
无
O
d
r
O
l
d
r
O
d
r
[知识梳理]
1、⊙O的半径为r ,圆心O到直线a 的距离为d
(1)r=4,d=3,则直线a与⊙O
(2)r=4,d=4,则直线a与⊙O
(3)若直线a与⊙O相离,r=4,则d的取值范围为
相交
相切
2、如图,Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
⊙C的半径为2.4cm,则⊙C与线段AB的位置关系为
C
B
A
d>4
相切
D
[小试牛刀]
C
B
A
变一变:如图,Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,⊙C与线段AB只有一个公共点,则⊙C半径r的取值范围是
[初露锋芒]
二、切线的判定方法
③切线的判定定理:
②比较法(d=r):
圆心的距离到直线等于圆的半径。
①定义法: 直线与圆只有一个公共点。
经过半径外端并且垂直于这条半径的直线是圆的切线。
[方法归类]
1、如图,线段AB经过圆心O,与⊙O交于点A、C,∠BAD=∠B=30°,边BD交圆于点D。那么BD是⊙O的切线吗?为什么?
O
A
B
C
D
答:BD是⊙O的切线
理由:连结OD,
∵∠BAD=∠B=30°
∴∠ADB=120°
又∵OA=OD
∴∠ODA=30°
∴∠ODB=90°
∴BD是⊙O的切线
[知识应用]
A
B
D
O
C
2、△ABC中,AB=AC,AO是底边BC上的中线,以O为圆心的圆与AB边相切,切点为D。
求证:⊙O也与AC边相切。
E
证明:过O作OE⊥AC于E。
∵AB=AC
又∵AO是BC边上的中线
∴AO是∠BAC的平分线
∵AB与⊙O相切
∴ OD⊥AB,
又∵ OE⊥AC
∴OE=OD
∴OE是⊙O的切线
[知识应用]
3、如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E。
由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
D
E
C
O
B
A
[拓展思维]
三、切线的性质
1、经过切点的半径垂直与圆的切线;
2、经过切点垂直于切线的直线必经过圆心。
A
B
O
T
[知识回放]
1、如图,A、B两点在⊙O上,AC是⊙O的切线,∠B=65°,则∠BAC=
2、已知,PA为⊙O的切线,A为切点,OP交⊙O于点B,PB=2,PA =4。则⊙O的半径r=
C
A
B
O
[练习巩固]
[综合强化]
3、已知:如图,CD切⊙O于D,割线CBA经过点O,
DE⊥AB,垂足为E。求证:∠1=∠2。
2
1
O
A
C
D
E
B
[盘点收获]
这一节课我们复习了哪些内容?
你掌握了哪些添辅助线的方法?
你最感兴趣的是哪些?
本课中涉及的数学思想有哪些?
1.:如图,正三角形ABC的边长为6 厘米,⊙O的半径为r厘米,当圆心O从点A出发,沿着线路AB一BC一CA运动,回到点A时,⊙O随着点O的运动而移动.在⊙O移动过程中,从切点的个数来考虑,相切有几种不同的情况?写出不同情况下,r的取值范围及相应的切点个数.
A
B
C
2.如图:菱形ABCD的边长为5cm,∠B=60°当以A为圆心的圆与BC相切时,半径是 ,此时⊙A与CD的位置关系是 。
3.如图,一热带风暴中心O距A岛为2千米,风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行,问∠BAO的度数是多少时船就会进入风暴影响圈?
4.如图,在直角梯形ABCD中,∠B=90°,AD∥BC, ∠C= 30° ,AD=1,AB=2.
试猜想在BC是否存在一点P,使得⊙P与线段CD、
AB都相切,如存在,请确定⊙P的半径.
挑战自我!
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q,A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动。设运动时间为t(s)。
(1)求PQ的长;
(2)当t为何值时,直线AB与⊙O相切?
[激荡思维]
.
B
P
A
Q
M
N
.
O
引申:当0.5﹤t﹤3.5时,你能否求出直线 AB被⊙O截得的弦长关于时间t的表达式?
