28.2.2直线与圆的位置关系(复习课)
文档属性
| 名称 | 28.2.2直线与圆的位置关系(复习课) |

|
|
| 格式 | rar | ||
| 文件大小 | 931.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-25 00:00:00 | ||
图片预览



文档简介
(共27张PPT)
1.直线与圆的位置关系有几种
A
o
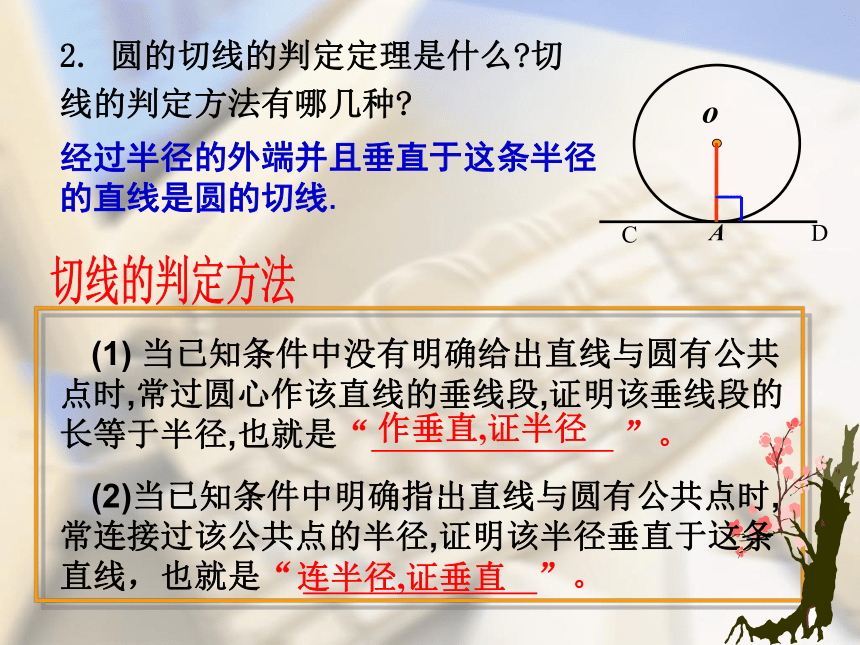
2. 圆的切线的判定定理是什么 切线的判定方法有哪几种
(1) 当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径,也就是“ ”。
(2)当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,也就是“ ”。
经过半径的外端并且垂直于这条半径的直线是圆的切线.
C
D
作垂直,证半径
连半径,证垂直
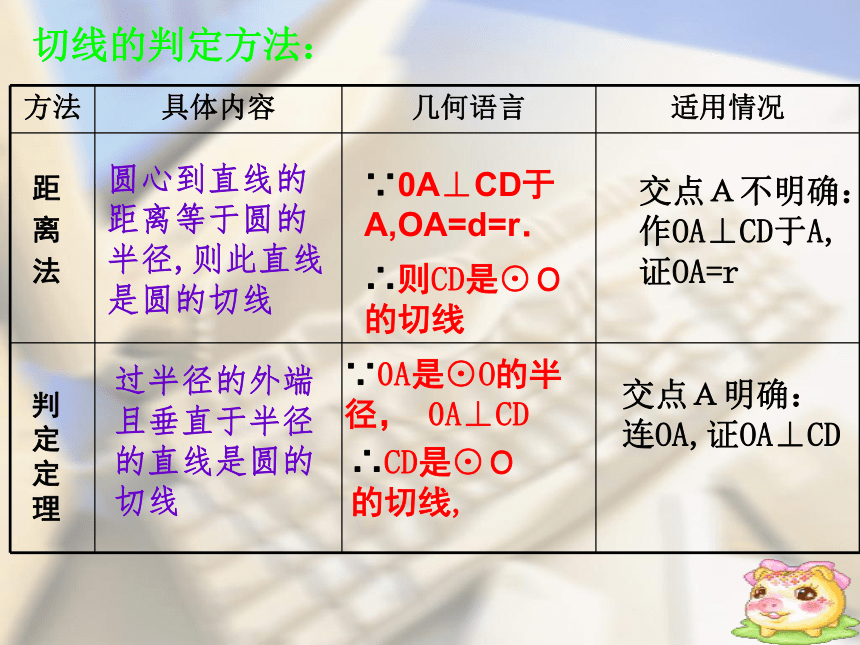
切线的判定方法:
方法 具体内容 几何语言 适用情况
距
离
法
判
定
定
理
圆心到直线的距离等于圆的半径,则此直线是圆的切线
过半径的外端且垂直于半径的直线是圆的切线
∵0A⊥CD于A,OA=d=r.
∴则CD是⊙O
的切线
交点A明确:
连OA,证OA⊥CD
交点A不明确:
作OA⊥CD于A,
证OA=r
∵0A是⊙O的半径, 0A⊥CD
∴CD是⊙O的切线,
3.切线有哪些性质
A
o
根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一
根据切线性质,我们经常做的辅助线是什么
(2)切线的性质定理:圆的切线垂直于过切点的半径.
符号语言: ∵CD是⊙O的切线,点A是切点
∴ OA⊥CD
C
D
(1)圆心到切线的距离等于半径
符号语言∵如图:CD与⊙O相切,OA⊥CD
∴d=OA=r
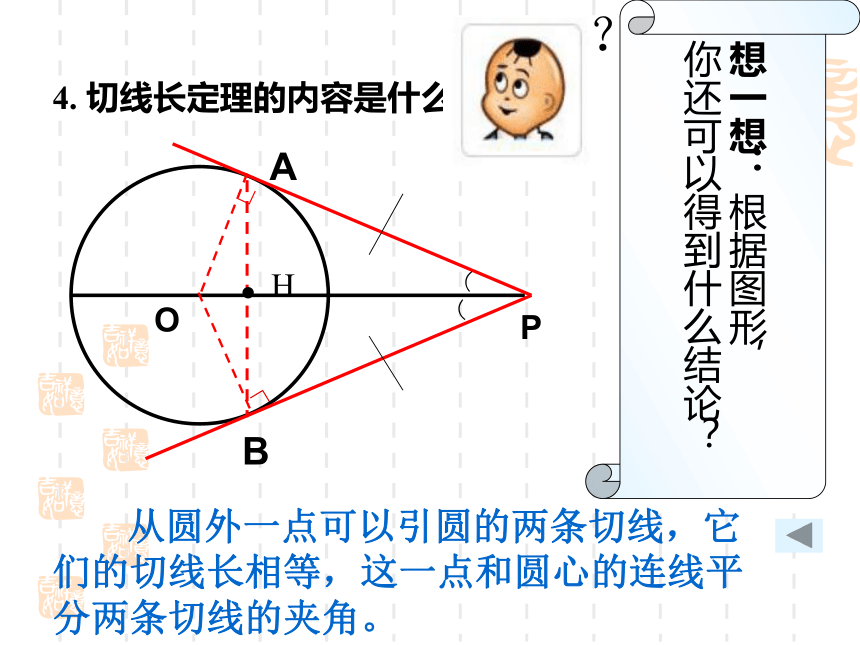
4. 切线长定理的内容是什么
∟
∟
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
P
A
B
想一想:根据图形,
你还可以得到什么结论?
. H
?
⌒
⌒
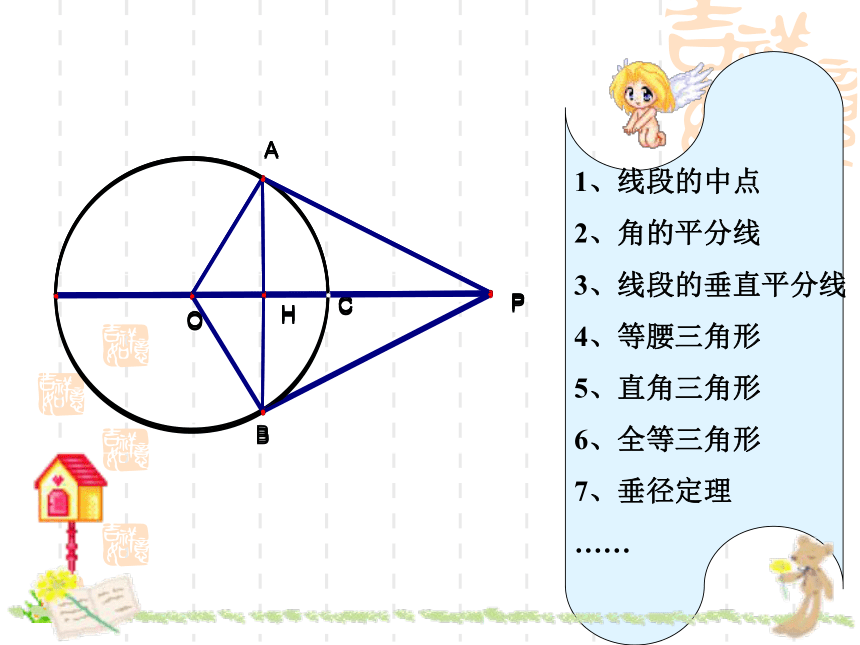
1、线段的中点
2、角的平分线
3、线段的垂直平分线
4、等腰三角形
5、直角三角形
6、全等三角形
7、垂径定理
……
?
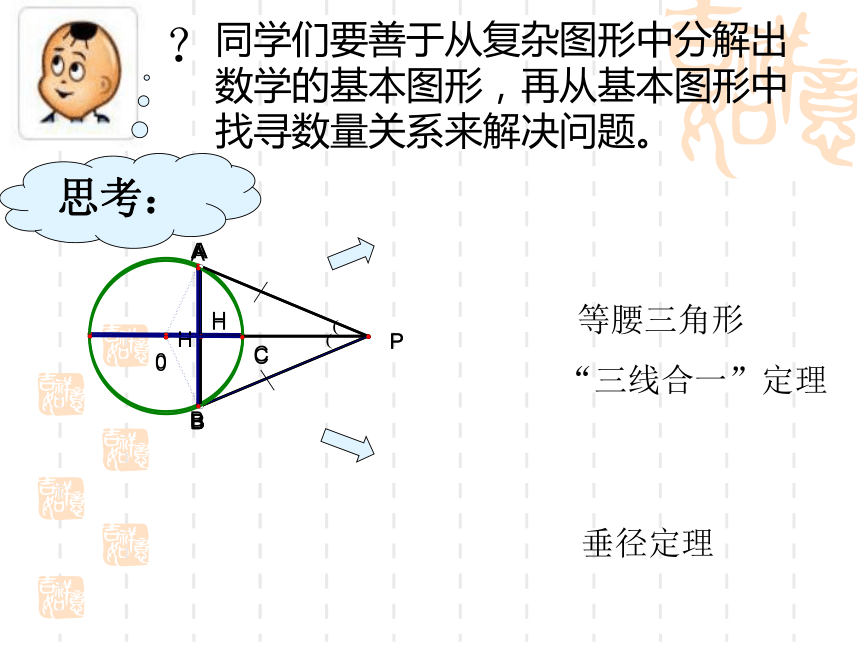
等腰三角形
“三线合一”定理
垂径定理
同学们要善于从复杂图形中分解出 数学的基本图形,再从基本图形中找寻数量关系来解决问题。
﹙
﹙
思考:
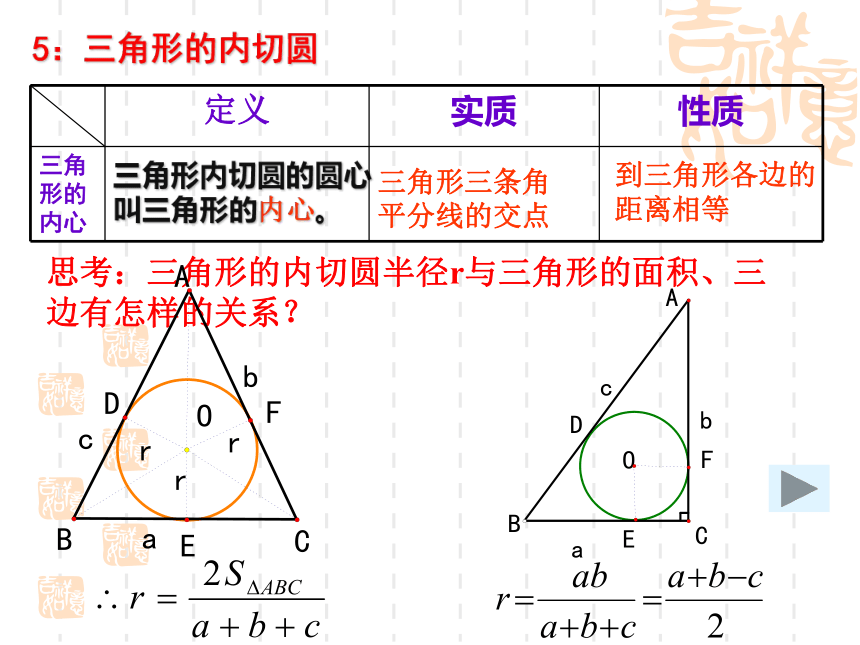
5:三角形的内切圆
三角形内切圆的圆心叫三角形的内心。
定义 实质 性质
三角形的内心
到三角形各边的距离相等
三角形三条角
平分线的交点
思考:三角形的内切圆半径r与三角形的面积、三边有怎样的关系?
思考:三角形的内切圆半径r与三角形的面积、三边有怎样的关系?
如图△ABC的三边分别为a、b、c,面积为S ⊙O分别与三边切于点D、E、F。试求内切圆半径r
解:连接OD、OE、OF、OA、OB、OC
∵ ⊙O分别与三边切于点D、E、F
∴OD⊥AB 、 OE ⊥BC、OF ⊥AC
OD=OE=OF=r
∴S△ABC= S△AOB +S△BOC +S△AOC
思考:直角三角形的内切圆半径r与三角形的三边有怎样的关系?
如图Rt△ABC的三边分别为a、b、c,∠C=90°,⊙O分别与三边切于点D、E、F。试求内切圆半径r
解:连接OE、OF
∵ ⊙O分别与三边切于点D、E、F
∴OE ⊥BC、OF ⊥AC,OE=OF=r
∵ ∠C=90°
∴四边形OECF是正方形
∴OE=CE=CF=OF=r
∴AD=AF=b-r
BD=BE=c-r
∴AB=b-r+c-r=C
例1.如图,点O是△ABC的内切圆的圆心。
(1)若∠BAC=80°,则∠BOC=___
130°
分析:根据三角形内切圆性质OB、OC分别平分∠ABC、ACB,要求∠BOC,只要求∠1+ ∠2 怎么求这两个角的和呢?
⌒
⌒
1
2
例1.如图,点O是△ABC的内切圆的圆心。
(2) ⊙O分别切AB、AC于点D、F,点P是优弧DF上一动点(点D、E除外),若∠BAC=80°,则∠DPF=__
⌒
思考:若点P是⊙O上的一动点(点D、F除外),上面的结论还成立吗?
根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一 .
50°
∟
∟
当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,也就是“连半径,证垂直”。
例2.如图:已知PA是⊙O的切线,A为切点, AB是⊙O 的直径 , BC//OP交⊙O于点C。求证:PC与⊙O相切.
解: 连接OC.
∵ OB=OC,
∴∠ OCB=∠OBC.
∴ ⊿POC ≌ ⊿POA(SAS)
∵ ⊙O切AP于A,
∴AB⊥PA.
∵ BC//OP,
∴∠ OCB=∠POC.
∠ OBC=∠POA.
∴∠POC=∠POA.
∵ OP=OP,OA=OB
∴∠ PCO=∠PAO.
∴∠ PCO= ∠ PAO= 900.
∴ PC是⊙O的切线.
∴ PC⊥半径OC于点C
。
直径所对的圆周角是直角 , 遇到直径 , 作直角 , 这也是圆中添加辅助线的常用方法之一
另解:如图:已知PA是⊙O的切线,A为切点, AB是⊙O 的直径 , BC//OP交⊙O于点C。求证:PC与⊙O相切.
当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,也就是“连半径,证垂直”。
。
直径所对的圆周角是直角 , 遇到直径 , 作直角 , 这也是圆中添加辅助线的常用方法之一
例2.如图:已知PA是⊙O的切线,A为切点, AB是⊙O 的直径 , 。求证: .
弦BC//OP
PC与⊙O相切
1、如图,已知PA、PC是⊙O的切线,A、C为切点, AB是⊙O 的直径 。求证: BC//OP
1、如图,已知PA、PC是⊙O的切线,A、C为切点, AB是⊙O 的直径 。求证: BC//OP
根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一 .
2、 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, E为AB的中点, 以AB为直径的圆与边CD相切于点F.求证:(1)DE⊥CE,(2)CD=AD+BC
A
B
C
D
E
F
我思考,我进步!
解: 连结EF
∵ ∠A= 900 , AB为⊙E的直径
∴ AD与⊙E相切.
∵ CD与⊙E相切.
∴ ∠ FDE= ∠ADC, AD=DF
1
2
同理得:∠ ECF= ∠BCD, CF=BC
1
2
∵ AD//BC
∴ ∠ADC+ ∠BCD=1800.
∴ ∠EDF+ ∠ECF=900.
∴ ∠DEC=900.
∴ CE⊥DE
∴ CD=DF+CF=AD+BC.
∴ CE⊥DE ,CD=AD+BC
3.(变式) 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, 且CD=AD+BC, 以AB为直径的圆
与边CD有怎样的位置关系,说明理由.
A
B
C
D
F
E
M
解: 以AB为直径的圆与CD相切.
方法一、取AB的中点E, 则点E即为以AB为直径的圆的圆心,过点E作 EF⊥CD 于 F,连接DE并延长交CB的延长线于点M……….
当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径.即“作垂直,证半径”.
A
B
C
D
F
当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径.即“作垂直,证半径”.
3.变式: 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, 且CD=AD+BC, 以AB为直径的圆与边CD有怎样的位置关系,说明理由.
A
B
C
D
F
E
解: 以AB为直径的圆与CD相切.
方法二、取AB的中点E, 则点E即为以AB为直径的圆的圆心,过点E作 EF⊥CD 于 F,,连接DE、EC…….
∟
∟
∟
面积相等法---构造等式
回顾与反思
同学们, 学习完本节课之后, 你有什么体会,谈谈你的想法,让大家分享一下你的思维成果!
驶向胜利的彼岸
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑴试猜想PC与⊙D的位置关系,并说明理由.
分析:做此类题,尤其强调
数形结合,同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证?联
想证明切线的两种方法。点
C在圆上,即证:∠DCP=90°
利用勾股及逆定理可得。
切
线
判
定
令x=0,得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5
又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20
在△CPD中, CD2+CP2=5+20=25, DP2=25
∴CD2+CP2=DP2
即:△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.
证明:∵直线y=-2x-4
解: PC是⊙O的切线,
勾股(逆)定理
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑵判断在直线PC上是否存在点E,使得S△EOC=
4S△CDO,若存在,求出点E的坐标;若不存在,
请说明理由.
存
在
性
问
题
解:假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO,
∵E点在直线PC:y=-2x-4上,
∴当y0=4时有:
当y0=-4时有:
∴在直线PC上存在满足条件的E点,其的坐标为(-4,4) , (0,-4) .
抓住不变量
分类讨论
1.直线与圆的位置关系有几种
A
o
2. 圆的切线的判定定理是什么 切线的判定方法有哪几种
(1) 当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径,也就是“ ”。
(2)当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,也就是“ ”。
经过半径的外端并且垂直于这条半径的直线是圆的切线.
C
D
作垂直,证半径
连半径,证垂直
切线的判定方法:
方法 具体内容 几何语言 适用情况
距
离
法
判
定
定
理
圆心到直线的距离等于圆的半径,则此直线是圆的切线
过半径的外端且垂直于半径的直线是圆的切线
∵0A⊥CD于A,OA=d=r.
∴则CD是⊙O
的切线
交点A明确:
连OA,证OA⊥CD
交点A不明确:
作OA⊥CD于A,
证OA=r
∵0A是⊙O的半径, 0A⊥CD
∴CD是⊙O的切线,
3.切线有哪些性质
A
o
根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一
根据切线性质,我们经常做的辅助线是什么
(2)切线的性质定理:圆的切线垂直于过切点的半径.
符号语言: ∵CD是⊙O的切线,点A是切点
∴ OA⊥CD
C
D
(1)圆心到切线的距离等于半径
符号语言∵如图:CD与⊙O相切,OA⊥CD
∴d=OA=r
4. 切线长定理的内容是什么
∟
∟
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
P
A
B
想一想:根据图形,
你还可以得到什么结论?
. H
?
⌒
⌒
1、线段的中点
2、角的平分线
3、线段的垂直平分线
4、等腰三角形
5、直角三角形
6、全等三角形
7、垂径定理
……
?
等腰三角形
“三线合一”定理
垂径定理
同学们要善于从复杂图形中分解出 数学的基本图形,再从基本图形中找寻数量关系来解决问题。
﹙
﹙
思考:
5:三角形的内切圆
三角形内切圆的圆心叫三角形的内心。
定义 实质 性质
三角形的内心
到三角形各边的距离相等
三角形三条角
平分线的交点
思考:三角形的内切圆半径r与三角形的面积、三边有怎样的关系?
思考:三角形的内切圆半径r与三角形的面积、三边有怎样的关系?
如图△ABC的三边分别为a、b、c,面积为S ⊙O分别与三边切于点D、E、F。试求内切圆半径r
解:连接OD、OE、OF、OA、OB、OC
∵ ⊙O分别与三边切于点D、E、F
∴OD⊥AB 、 OE ⊥BC、OF ⊥AC
OD=OE=OF=r
∴S△ABC= S△AOB +S△BOC +S△AOC
思考:直角三角形的内切圆半径r与三角形的三边有怎样的关系?
如图Rt△ABC的三边分别为a、b、c,∠C=90°,⊙O分别与三边切于点D、E、F。试求内切圆半径r
解:连接OE、OF
∵ ⊙O分别与三边切于点D、E、F
∴OE ⊥BC、OF ⊥AC,OE=OF=r
∵ ∠C=90°
∴四边形OECF是正方形
∴OE=CE=CF=OF=r
∴AD=AF=b-r
BD=BE=c-r
∴AB=b-r+c-r=C
例1.如图,点O是△ABC的内切圆的圆心。
(1)若∠BAC=80°,则∠BOC=___
130°
分析:根据三角形内切圆性质OB、OC分别平分∠ABC、ACB,要求∠BOC,只要求∠1+ ∠2 怎么求这两个角的和呢?
⌒
⌒
1
2
例1.如图,点O是△ABC的内切圆的圆心。
(2) ⊙O分别切AB、AC于点D、F,点P是优弧DF上一动点(点D、E除外),若∠BAC=80°,则∠DPF=__
⌒
思考:若点P是⊙O上的一动点(点D、F除外),上面的结论还成立吗?
根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一 .
50°
∟
∟
当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,也就是“连半径,证垂直”。
例2.如图:已知PA是⊙O的切线,A为切点, AB是⊙O 的直径 , BC//OP交⊙O于点C。求证:PC与⊙O相切.
解: 连接OC.
∵ OB=OC,
∴∠ OCB=∠OBC.
∴ ⊿POC ≌ ⊿POA(SAS)
∵ ⊙O切AP于A,
∴AB⊥PA.
∵ BC//OP,
∴∠ OCB=∠POC.
∠ OBC=∠POA.
∴∠POC=∠POA.
∵ OP=OP,OA=OB
∴∠ PCO=∠PAO.
∴∠ PCO= ∠ PAO= 900.
∴ PC是⊙O的切线.
∴ PC⊥半径OC于点C
。
直径所对的圆周角是直角 , 遇到直径 , 作直角 , 这也是圆中添加辅助线的常用方法之一
另解:如图:已知PA是⊙O的切线,A为切点, AB是⊙O 的直径 , BC//OP交⊙O于点C。求证:PC与⊙O相切.
当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,也就是“连半径,证垂直”。
。
直径所对的圆周角是直角 , 遇到直径 , 作直角 , 这也是圆中添加辅助线的常用方法之一
例2.如图:已知PA是⊙O的切线,A为切点, AB是⊙O 的直径 , 。求证: .
弦BC//OP
PC与⊙O相切
1、如图,已知PA、PC是⊙O的切线,A、C为切点, AB是⊙O 的直径 。求证: BC//OP
1、如图,已知PA、PC是⊙O的切线,A、C为切点, AB是⊙O 的直径 。求证: BC//OP
根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一 .
2、 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, E为AB的中点, 以AB为直径的圆与边CD相切于点F.求证:(1)DE⊥CE,(2)CD=AD+BC
A
B
C
D
E
F
我思考,我进步!
解: 连结EF
∵ ∠A= 900 , AB为⊙E的直径
∴ AD与⊙E相切.
∵ CD与⊙E相切.
∴ ∠ FDE= ∠ADC, AD=DF
1
2
同理得:∠ ECF= ∠BCD, CF=BC
1
2
∵ AD//BC
∴ ∠ADC+ ∠BCD=1800.
∴ ∠EDF+ ∠ECF=900.
∴ ∠DEC=900.
∴ CE⊥DE
∴ CD=DF+CF=AD+BC.
∴ CE⊥DE ,CD=AD+BC
3.(变式) 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, 且CD=AD+BC, 以AB为直径的圆
与边CD有怎样的位置关系,说明理由.
A
B
C
D
F
E
M
解: 以AB为直径的圆与CD相切.
方法一、取AB的中点E, 则点E即为以AB为直径的圆的圆心,过点E作 EF⊥CD 于 F,连接DE并延长交CB的延长线于点M……….
当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径.即“作垂直,证半径”.
A
B
C
D
F
当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径.即“作垂直,证半径”.
3.变式: 如图, 直角梯形ABCD中 , ∠A=900 , AD//BC, 且CD=AD+BC, 以AB为直径的圆与边CD有怎样的位置关系,说明理由.
A
B
C
D
F
E
解: 以AB为直径的圆与CD相切.
方法二、取AB的中点E, 则点E即为以AB为直径的圆的圆心,过点E作 EF⊥CD 于 F,,连接DE、EC…….
∟
∟
∟
面积相等法---构造等式
回顾与反思
同学们, 学习完本节课之后, 你有什么体会,谈谈你的想法,让大家分享一下你的思维成果!
驶向胜利的彼岸
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑴试猜想PC与⊙D的位置关系,并说明理由.
分析:做此类题,尤其强调
数形结合,同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证?联
想证明切线的两种方法。点
C在圆上,即证:∠DCP=90°
利用勾股及逆定理可得。
切
线
判
定
令x=0,得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5
又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20
在△CPD中, CD2+CP2=5+20=25, DP2=25
∴CD2+CP2=DP2
即:△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.
证明:∵直线y=-2x-4
解: PC是⊙O的切线,
勾股(逆)定理
已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑵判断在直线PC上是否存在点E,使得S△EOC=
4S△CDO,若存在,求出点E的坐标;若不存在,
请说明理由.
存
在
性
问
题
解:假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO,
∵E点在直线PC:y=-2x-4上,
∴当y0=4时有:
当y0=-4时有:
∴在直线PC上存在满足条件的E点,其的坐标为(-4,4) , (0,-4) .
抓住不变量
分类讨论
