6.2立方根 第2课时用计算器求算术平方根及其大小比较-人教版七年级下册课件(23张PPT)
文档属性
| 名称 | 6.2立方根 第2课时用计算器求算术平方根及其大小比较-人教版七年级下册课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 536.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 14:48:41 | ||
图片预览








文档简介
实
制作:Anan
数
知识回顾
3、平方根和立方根?
被开方数
平方根
立方根
正数
负数
零
有两个,互为相反数
无平方根
零
有一个,是正数
有一个,是负数
零
知识回顾
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是_________.平方根是它本身的数是_____算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
用计算器求算术平方根及其大小比较
6.1(第二课时)
学习目标
1、用计算器求立方根
2、探究立方根大小的变化规律
3、能够利用有理数估计无理数的值
4、能够求解简单的一元三次方程.
学习目标:
新课导入
1.任何有理数都有立方根,它不是正数就是负数
2.非负数的立方根还是非负数
3.一个数的平方根与其立方根相同,则这个数是1
不可能是负数
一个数的立方根有两个,它们互为相反数
x
√
x
x
x
讲授新知
一、用计算器求立方根
例1、用计算器求1845的立方根
依次按键
1845
=
显示:12.264 940 82
讲授新知
例2、用计算器求 的值(计算结果保留4位有效数字)。
1.354
=
按 键
显 示
2ndF
0.
1.354
1.106299938
解:用计算器求 的步骤如下:
∵计算结果要求保留4位有效数字,
讲授新知
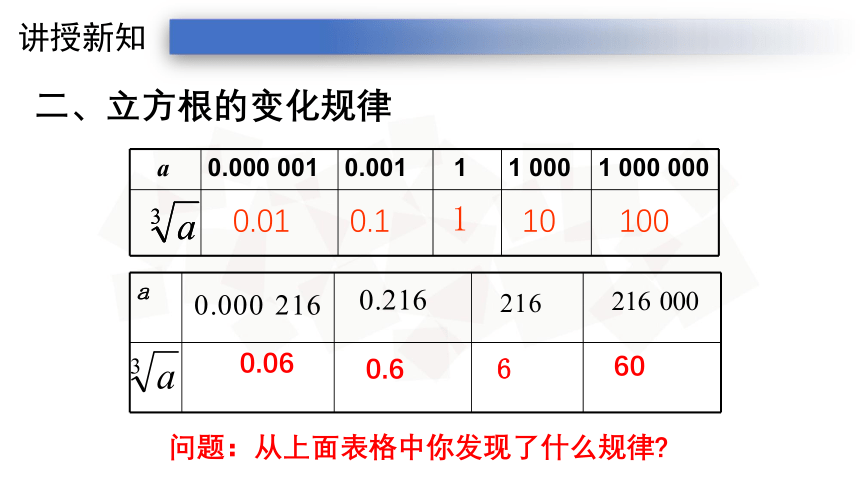
二、立方根的变化规律
a
0.000 001
0.001
1
1 000
1 000 000
0.1
1
10
100
a
60
0.01
问题:从上面表格中你发现了什么规律?
6
0.6
0.06
讲授新知
归纳:被开方数的小数点每向右(或左)移动三位,开方后立方根的小数点就向右(或左)移动一位。
观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍。
反之也成立。
1
10
0.1
1000
10
1000
10
讲授新知
例3、用你发现的规律填空
1.1
110
60
0.6
2
讲授新知
三、利用有理数估计无理数的值
例4、估计3,4, 的大小.
解:
Q
27 50 64,
< <
讲授新知
例5、比较下列各组数的大小.
解:
解:
讲授新知
四、求解简单的一元三次方程
例6、你能求出下列各式中的未知数x吗?
(1)x3+27=0; (2)125x3-64=0; (3)2(x+1)3-16=0.
解: (1) x3+27=0.
∴x=-3.
x3=-27.
(2) 125x3-64=0.
∴x=
讲授新知
x+1=2.
∴x=1.
解:(3) 2(x+1)3-16=0.
2(x+1)3=16
(x+1)3=8
讲授新知
三、立方根的特征
因为 = ,
所以
因为
所以
-2
=
=
-2
-3
-3
例2:填空,你能发现其中的规律吗?
讲授新知
一般地
即求负数的立方根,可以先求出这个负数的绝对值的立方根,再取其相反数。
讲授新知
四、平方根和立方根
被开方数
平方根
立方根
正数
负数
零
有两个,互为相反数
无平方根
零
有一个,是正数
有一个,是负数
零
课堂小结
1、用计算器求一个数的立方根.
2、比较无理数的大小.
3、求解简单一元三次方程.
随堂测试
——————。
——————。
——————。
=
=
=
0.06993
-324.6
-0.1507
随堂测试
3280
328000
3.估计68的立方根的大小在( )
A、2与3之间
B、3与4之间
C、4与5之间
D、5与6之间
C
随堂测试
4.一个正方体的水晶砖,体积为100cm?,
它的棱长大约在 ( )
A、4㎝~5㎝之间
C、6㎝~7㎝之间
B、5cm~6cm之间
D、7㎝~8㎝之间
A
THANKS
谢谢观看!
制作:Anan
数
知识回顾
3、平方根和立方根?
被开方数
平方根
立方根
正数
负数
零
有两个,互为相反数
无平方根
零
有一个,是正数
有一个,是负数
零
知识回顾
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是_________.平方根是它本身的数是_____算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
用计算器求算术平方根及其大小比较
6.1(第二课时)
学习目标
1、用计算器求立方根
2、探究立方根大小的变化规律
3、能够利用有理数估计无理数的值
4、能够求解简单的一元三次方程.
学习目标:
新课导入
1.任何有理数都有立方根,它不是正数就是负数
2.非负数的立方根还是非负数
3.一个数的平方根与其立方根相同,则这个数是1
不可能是负数
一个数的立方根有两个,它们互为相反数
x
√
x
x
x
讲授新知
一、用计算器求立方根
例1、用计算器求1845的立方根
依次按键
1845
=
显示:12.264 940 82
讲授新知
例2、用计算器求 的值(计算结果保留4位有效数字)。
1.354
=
按 键
显 示
2ndF
0.
1.354
1.106299938
解:用计算器求 的步骤如下:
∵计算结果要求保留4位有效数字,
讲授新知
二、立方根的变化规律
a
0.000 001
0.001
1
1 000
1 000 000
0.1
1
10
100
a
60
0.01
问题:从上面表格中你发现了什么规律?
6
0.6
0.06
讲授新知
归纳:被开方数的小数点每向右(或左)移动三位,开方后立方根的小数点就向右(或左)移动一位。
观察下面的运算,请你找出其中的规律
规律是:
①被开方数每扩大 倍,其结果就扩大 倍;
②被开方数每缩小 倍,其结果就缩小 倍。
反之也成立。
1
10
0.1
1000
10
1000
10
讲授新知
例3、用你发现的规律填空
1.1
110
60
0.6
2
讲授新知
三、利用有理数估计无理数的值
例4、估计3,4, 的大小.
解:
Q
27 50 64,
< <
讲授新知
例5、比较下列各组数的大小.
解:
解:
讲授新知
四、求解简单的一元三次方程
例6、你能求出下列各式中的未知数x吗?
(1)x3+27=0; (2)125x3-64=0; (3)2(x+1)3-16=0.
解: (1) x3+27=0.
∴x=-3.
x3=-27.
(2) 125x3-64=0.
∴x=
讲授新知
x+1=2.
∴x=1.
解:(3) 2(x+1)3-16=0.
2(x+1)3=16
(x+1)3=8
讲授新知
三、立方根的特征
因为 = ,
所以
因为
所以
-2
=
=
-2
-3
-3
例2:填空,你能发现其中的规律吗?
讲授新知
一般地
即求负数的立方根,可以先求出这个负数的绝对值的立方根,再取其相反数。
讲授新知
四、平方根和立方根
被开方数
平方根
立方根
正数
负数
零
有两个,互为相反数
无平方根
零
有一个,是正数
有一个,是负数
零
课堂小结
1、用计算器求一个数的立方根.
2、比较无理数的大小.
3、求解简单一元三次方程.
随堂测试
——————。
——————。
——————。
=
=
=
0.06993
-324.6
-0.1507
随堂测试
3280
328000
3.估计68的立方根的大小在( )
A、2与3之间
B、3与4之间
C、4与5之间
D、5与6之间
C
随堂测试
4.一个正方体的水晶砖,体积为100cm?,
它的棱长大约在 ( )
A、4㎝~5㎝之间
C、6㎝~7㎝之间
B、5cm~6cm之间
D、7㎝~8㎝之间
A
THANKS
谢谢观看!
