6.1平方根 第2课时用计算器求算术平方根及其大小比较-人教版七年级下册课件(18张PPT)
文档属性
| 名称 | 6.1平方根 第2课时用计算器求算术平方根及其大小比较-人教版七年级下册课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 14:48:55 | ||
图片预览






文档简介
实
制作:Anan
数
知识回顾
2.判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
-36
,
0.09
,
,
0
,
2
,
.
-36没有算术平方根.
只有非负数才有算术平方根,算术平方根是非负的.
1.什么是算术平方根?
用计算器求算术平方根及其大小比较
6.1(第二课时)
学习目标
1、用有理数估计无理数的大致范围
2、初步体验“无限不循环小数”的含义
3、用计算器求一个非负数的算术平方根
学习目标:
新课导入
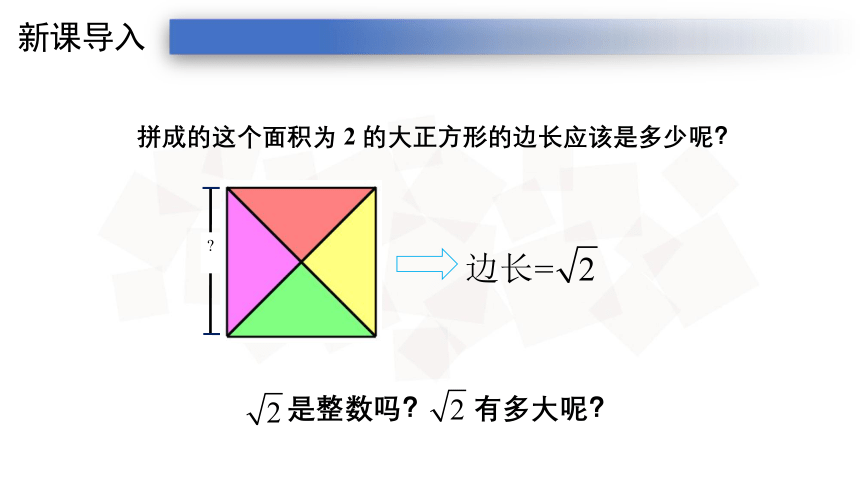
拼成的这个面积为
2
的大正方形的边长应该是多少呢?
是整数吗?
有多大呢?
?
讲授新知
一、无限不循环小数的概念
有多大呢?
大于1而小于2
你是怎样判断出
大于1而小于2的?
你能不能得到
的更精确的范围?
因为
,
,
而
<
<
,
所以
。
讲授新知
w
讲授新知
如此下去,可以得到
的更精确的近似值.
你以前见过这种数吗?
讲授新知
事实上,继续重复上述的过程,可以得到
小数位数无限,且小数部分不循环
是一个无限不循环的小数
小数位数无限,且小数部分不循环的小数称为无限不循环小数。
π也是一个无限不循环的小数
讲授新知
例1:估算
-2的值
( )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
解析:因为42<19<52,所以4<√19<5,所以2<√19-2<3.
故选B.
B
归纳:估计一个有理数的算术平方根的近似值,必须先判断这个有理数位于哪两个数的平方之间
讲授新知
二、用计算器求算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
a
=
按键顺序:
讲授新知
例2:用计算器求下列各式的值:
(1)
;
(2)
(精确到0.001)。
讲授新知
三、算术平方根的规律
利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律?你能说出其中的道理吗?
…
…
…
…
规律:被开方数的小数点向右每移动
位,它的算术平方根的小数点就向右移动
位;被开方数的小数点向左每移动
位,它的算术平方根的小数点就向左移动
位。
2
2
1
1
讲授新知
例3:你能用计算器计算
(精确到0.001)吗?并利用刚才的得到规律说出
,
,
的近似值。
≈1.732
≈0.1732
≈17.32
≈173.2
课堂小结
1、用有理数估计无理数的大致范围
2、
“无限不循环小数”的概念
3、用计算器求算术平方根
4、算术平方根运算中的规律
随堂测试
(1)144的算数平方根是________;
(2)1的算数平方根是________;
(3)
的算数平方根是________;
(4)0.008
1的算数平方根是________;
(5)5的算数平方根是________;
(6)
的算数平方根是________.
12
1
4/5
0.09
√5
3/2
1、求下列各数的算术平方根
随堂测试
2、2m+2的算数平方根是4,3m+n+1的算数平方根是5,求m+2n的值.
解:∵2m+2的算数平方根是4,3m+n+1的算数平方根是5,
∴2m+2=16,3m+n+1=25,
联立解得,m=7,n=3,
∴m+2n=7+2×3=13.
答:m+2n的值为13.
THANKS
谢谢观看!
制作:Anan
数
知识回顾
2.判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
-36
,
0.09
,
,
0
,
2
,
.
-36没有算术平方根.
只有非负数才有算术平方根,算术平方根是非负的.
1.什么是算术平方根?
用计算器求算术平方根及其大小比较
6.1(第二课时)
学习目标
1、用有理数估计无理数的大致范围
2、初步体验“无限不循环小数”的含义
3、用计算器求一个非负数的算术平方根
学习目标:
新课导入
拼成的这个面积为
2
的大正方形的边长应该是多少呢?
是整数吗?
有多大呢?
?
讲授新知
一、无限不循环小数的概念
有多大呢?
大于1而小于2
你是怎样判断出
大于1而小于2的?
你能不能得到
的更精确的范围?
因为
,
,
而
<
<
,
所以
。
讲授新知
w
讲授新知
如此下去,可以得到
的更精确的近似值.
你以前见过这种数吗?
讲授新知
事实上,继续重复上述的过程,可以得到
小数位数无限,且小数部分不循环
是一个无限不循环的小数
小数位数无限,且小数部分不循环的小数称为无限不循环小数。
π也是一个无限不循环的小数
讲授新知
例1:估算
-2的值
( )
A.在1和2之间
B.在2和3之间
C.在3和4之间
D.在4和5之间
解析:因为42<19<52,所以4<√19<5,所以2<√19-2<3.
故选B.
B
归纳:估计一个有理数的算术平方根的近似值,必须先判断这个有理数位于哪两个数的平方之间
讲授新知
二、用计算器求算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
a
=
按键顺序:
讲授新知
例2:用计算器求下列各式的值:
(1)
;
(2)
(精确到0.001)。
讲授新知
三、算术平方根的规律
利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律?你能说出其中的道理吗?
…
…
…
…
规律:被开方数的小数点向右每移动
位,它的算术平方根的小数点就向右移动
位;被开方数的小数点向左每移动
位,它的算术平方根的小数点就向左移动
位。
2
2
1
1
讲授新知
例3:你能用计算器计算
(精确到0.001)吗?并利用刚才的得到规律说出
,
,
的近似值。
≈1.732
≈0.1732
≈17.32
≈173.2
课堂小结
1、用有理数估计无理数的大致范围
2、
“无限不循环小数”的概念
3、用计算器求算术平方根
4、算术平方根运算中的规律
随堂测试
(1)144的算数平方根是________;
(2)1的算数平方根是________;
(3)
的算数平方根是________;
(4)0.008
1的算数平方根是________;
(5)5的算数平方根是________;
(6)
的算数平方根是________.
12
1
4/5
0.09
√5
3/2
1、求下列各数的算术平方根
随堂测试
2、2m+2的算数平方根是4,3m+n+1的算数平方根是5,求m+2n的值.
解:∵2m+2的算数平方根是4,3m+n+1的算数平方根是5,
∴2m+2=16,3m+n+1=25,
联立解得,m=7,n=3,
∴m+2n=7+2×3=13.
答:m+2n的值为13.
THANKS
谢谢观看!
