1.2直角三角形 培优训练-2020-2021学年北师大版八年级数学下册(Word版 含答案)
文档属性
| 名称 | 1.2直角三角形 培优训练-2020-2021学年北师大版八年级数学下册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 366.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览


文档简介
北师版八年级下册数学第一章 三角形的证明
第2节《直角三角形》同步培优训练
选择。
1.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是 ( )
?
A.20 B.20 C.30 D.10?
2.在Rt△ABC中,∠C=90°,∠A=30°,AB=4,那么( )
A.BC=8 B.AC=2 C.AC= D.BC=
3.如图,在中,AB=AC, ∠B=30°,AD⊥AB,AD=4,则下列各式中正确的是( )
A.AB=8 B.BC=16 C.DC=4 D.BD=10
4.如图,的三个内角比为1:1:2,且,则∠CBD是( )
A.5° B.10° C.15° D.45°
5.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高
度为尺,则可列方程为( )
A. B.
C. D.
6.如图,有一块直角三角形纸片,两直角边,.现将直角边沿直线折叠,使它落在斜边上,且与重合,则等于( )
A. B. C. D.
7.下列命题中,是假命题的是( )
A.在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C.在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D.在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
8.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
A. B. C. D.
9.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
A.600m B.500m
C.400m D.300m
10.若直角三角形的三边长分别为、a、,且a、b都是正整数,则三角形其中一边的长可能为()
A.22 B.32 C.62 D.82
填空。
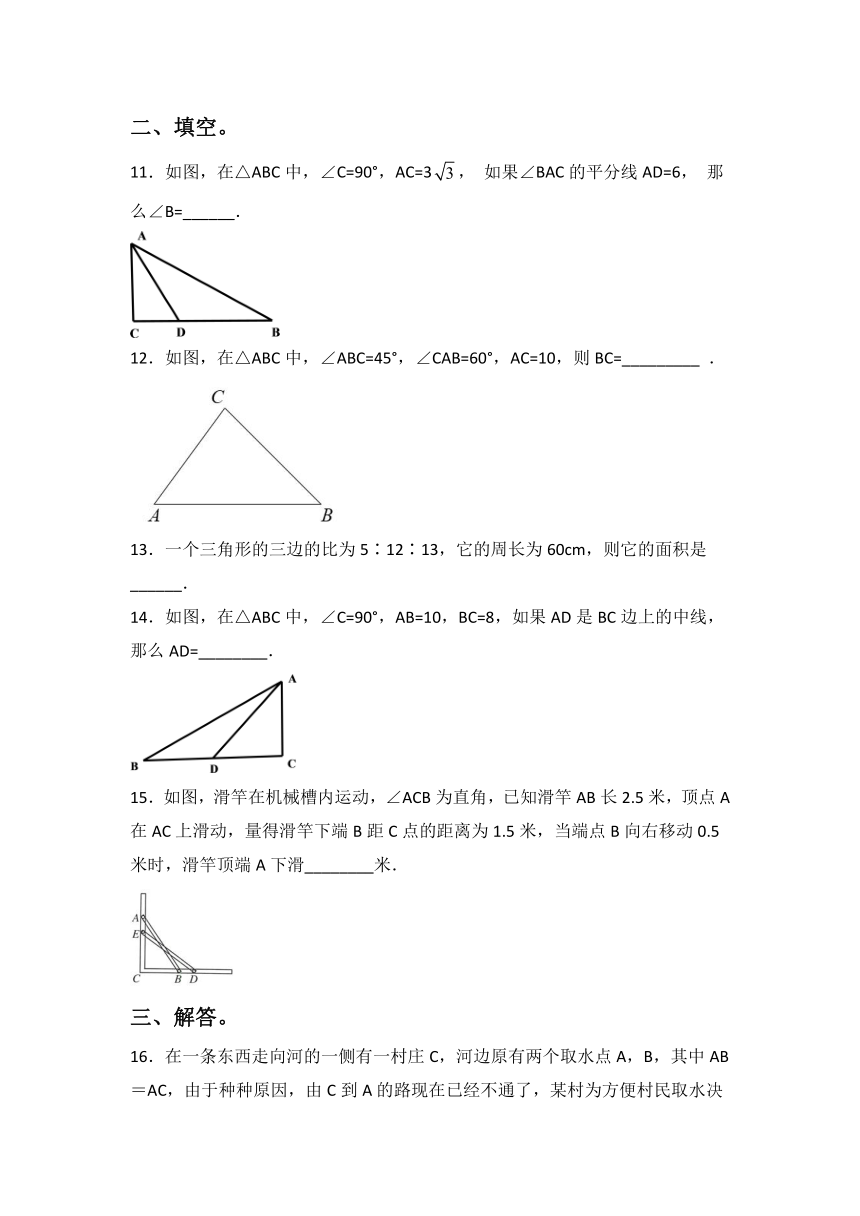
11.如图,在△ABC中,∠C=90°,AC=3, 如果∠BAC的平分线AD=6, 那么∠B=______.
12.如图,在△ABC中,∠ABC=45°,∠CAB=60°,AC=10,则BC=_________ .
13.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是______.
14.如图,在△ABC中,∠C=90°,AB=10,BC=8,如果AD是BC边上的中线,那么AD=________.
15.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.
解答。
16.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于种种原因,由C到A的路现在已经不通了,某村为方便村民取水决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是不是从村庄C到河边的最近路,请通过计算加以说明;
(2)求原来的路线AC的长.
17.如图所示,在△ABC中,AC=8cm,BC=6cm;在△ABE中,DE为AB边上的高,DE=12cm,△ABE的面积S=60cm2.
(1)求出AB边的长;
(2)你能求出∠C的度数吗?请试一试.
18.如图,在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:.
19.如图,三个村庄A、B、C之间的距离分别为AB=12km,AC=5km,BC=13km,要从A修一条公路AD直达BC,已知公路的造价为26000元/km,求这条公路的最低造价是多少万元?
20.如图,在中,,,,.
求的周长;
判断是否是直角三角形,并说明理由.
答案
1-5:DCCCD 6-10:BCDBB
11.30°
12.
13.
14.
15.0.5
16.(1)是,理由见解析;(2)2.5米.
(1)∵,即,
∴Rt△CHB是直角三角形,即CH⊥BH,
∴CH是从村庄C到河边的最近路(点到直线的距离中,垂线段最短);
(2)设AC=AB=x,则AH=x-1.8,
∵在Rt△ACH,
∴,即 ,解得x=2.5,
∴原来的路线AC的长为2.5米.
17.(1)AB=10;(2)∠C=90°.
(1)∵DE=12,S△ABE= DE?AB=60,
∴AB=10;
(2)∵AC=8,BC=6,62+82=102,
∴AC2+BC2=AB2,
由勾股定理逆定理得∠C=90°.
18.
证明:连接MA,
∵MD⊥AB,
∴AD2=AM2-MD2,BM2=BD2+MD2,
∵∠C=90°,
∴AM2=AC2+CM2
∵M为BC中点,
∴BM=MC.
∴AD2=AC2+BD2
19.最低造价为120000元.
20.(1)54;(2)不是直角三角形,理由见解析.
解:,
.
在和中,
根据勾股定理得,,
又,,,
,
;
不是直角三角形.理由:
,
,
不是直角三角形.
第2节《直角三角形》同步培优训练
选择。
1.如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是 ( )
?
A.20 B.20 C.30 D.10?
2.在Rt△ABC中,∠C=90°,∠A=30°,AB=4,那么( )
A.BC=8 B.AC=2 C.AC= D.BC=
3.如图,在中,AB=AC, ∠B=30°,AD⊥AB,AD=4,则下列各式中正确的是( )
A.AB=8 B.BC=16 C.DC=4 D.BD=10
4.如图,的三个内角比为1:1:2,且,则∠CBD是( )
A.5° B.10° C.15° D.45°
5.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高
度为尺,则可列方程为( )
A. B.
C. D.
6.如图,有一块直角三角形纸片,两直角边,.现将直角边沿直线折叠,使它落在斜边上,且与重合,则等于( )
A. B. C. D.
7.下列命题中,是假命题的是( )
A.在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C.在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D.在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
8.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
A. B. C. D.
9.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
A.600m B.500m
C.400m D.300m
10.若直角三角形的三边长分别为、a、,且a、b都是正整数,则三角形其中一边的长可能为()
A.22 B.32 C.62 D.82
填空。
11.如图,在△ABC中,∠C=90°,AC=3, 如果∠BAC的平分线AD=6, 那么∠B=______.
12.如图,在△ABC中,∠ABC=45°,∠CAB=60°,AC=10,则BC=_________ .
13.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是______.
14.如图,在△ABC中,∠C=90°,AB=10,BC=8,如果AD是BC边上的中线,那么AD=________.
15.如图,滑竿在机械槽内运动,∠ACB为直角,已知滑竿AB长2.5米,顶点A在AC上滑动,量得滑竿下端B距C点的距离为1.5米,当端点B向右移动0.5米时,滑竿顶端A下滑________米.
解答。
16.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于种种原因,由C到A的路现在已经不通了,某村为方便村民取水决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是不是从村庄C到河边的最近路,请通过计算加以说明;
(2)求原来的路线AC的长.
17.如图所示,在△ABC中,AC=8cm,BC=6cm;在△ABE中,DE为AB边上的高,DE=12cm,△ABE的面积S=60cm2.
(1)求出AB边的长;
(2)你能求出∠C的度数吗?请试一试.
18.如图,在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:.
19.如图,三个村庄A、B、C之间的距离分别为AB=12km,AC=5km,BC=13km,要从A修一条公路AD直达BC,已知公路的造价为26000元/km,求这条公路的最低造价是多少万元?
20.如图,在中,,,,.
求的周长;
判断是否是直角三角形,并说明理由.
答案
1-5:DCCCD 6-10:BCDBB
11.30°
12.
13.
14.
15.0.5
16.(1)是,理由见解析;(2)2.5米.
(1)∵,即,
∴Rt△CHB是直角三角形,即CH⊥BH,
∴CH是从村庄C到河边的最近路(点到直线的距离中,垂线段最短);
(2)设AC=AB=x,则AH=x-1.8,
∵在Rt△ACH,
∴,即 ,解得x=2.5,
∴原来的路线AC的长为2.5米.
17.(1)AB=10;(2)∠C=90°.
(1)∵DE=12,S△ABE= DE?AB=60,
∴AB=10;
(2)∵AC=8,BC=6,62+82=102,
∴AC2+BC2=AB2,
由勾股定理逆定理得∠C=90°.
18.
证明:连接MA,
∵MD⊥AB,
∴AD2=AM2-MD2,BM2=BD2+MD2,
∵∠C=90°,
∴AM2=AC2+CM2
∵M为BC中点,
∴BM=MC.
∴AD2=AC2+BD2
19.最低造价为120000元.
20.(1)54;(2)不是直角三角形,理由见解析.
解:,
.
在和中,
根据勾股定理得,,
又,,,
,
;
不是直角三角形.理由:
,
,
不是直角三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
