2020-2021学年北师大版数学八年级下册第一章《三角形的证明》第三节:1.3.1线段垂直平分线(第一课时)(共17张)
文档属性
| 名称 | 2020-2021学年北师大版数学八年级下册第一章《三角形的证明》第三节:1.3.1线段垂直平分线(第一课时)(共17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 18:06:34 | ||
图片预览





文档简介
北师大版八年级(下)
1.3线段垂直平分线
第一章 三角形的证明
第1回 线段垂直平分线的性质和判定
学习目标
1.探索证明线段垂直平分线的性质和判定.
2.能运用线段垂直平分线性质和其判定解决实际问题.
3.经历“探索-发现-猜想-证明”的过程,进一步体会证明的必要性,增强证明意识和能力,发展推理能力.
课前复习
1.等边对等角,等角对等边,逆命题,逆定理,难我不倒;
2.“三线合一”,反证法,熟能生巧;
3.不论勾股定理,还是倒过来作为判定,外加特殊全等判定(HL),小到两锐角互余,一条不会漏掉.
不论等腰还是直角,你我皆已明了!
想一想:曾经我们用折纸的办法得出“线段垂直平分线线上的点到线段两个端点距离相等”,有了前面两节证明的经验积累,你现在一定可以证明这一结论.
聪明如我的你们
一定可以搞定哦!
画图试试!
新知探究
新知探究
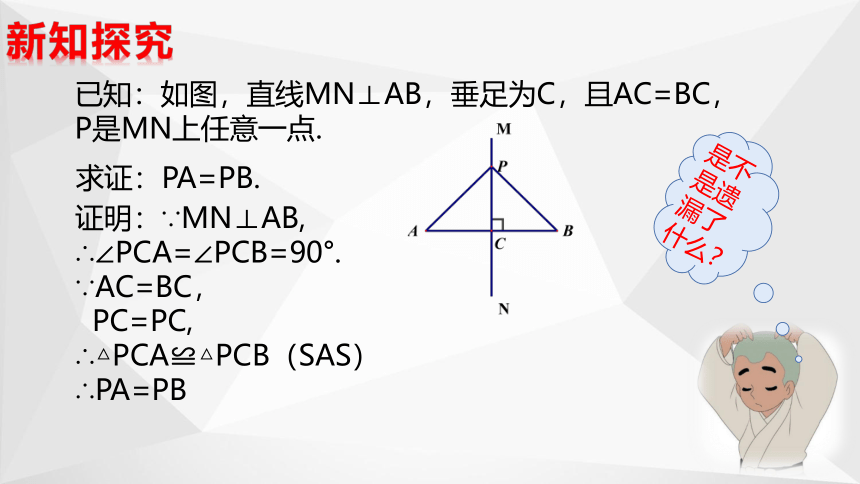
已知:如图,直线MN⊥AB,垂足为C,且AC=BC,P是MN上任意一点.
求证:PA=PB.
证明:∵MN⊥AB,
∴∠PCA=∠PCB=90°.
∵AC=BC,
PC=PC,
∴△PCA≌△PCB(SAS)
∴PA=PB
是不是遗漏了什么?
新知探究
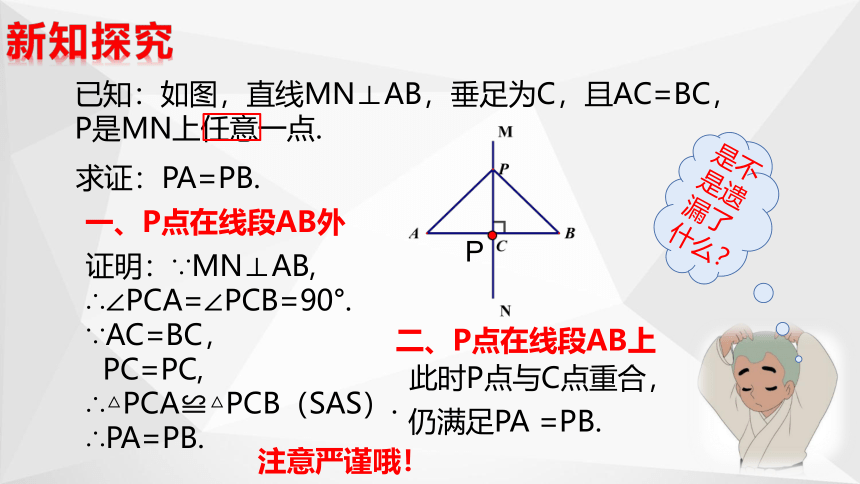
已知:如图,直线MN⊥AB,垂足为C,且AC=BC,P是MN上任意一点.
求证:PA=PB.
证明:∵MN⊥AB,
∴∠PCA=∠PCB=90°.
∵AC=BC,
PC=PC,
∴△PCA≌△PCB(SAS).
∴PA=PB.
是不是遗漏了什么?
一、P点在线段AB外
二、P点在线段AB上
此时P点与C点重合,
仍满足PA =PB.
P
注意严谨哦!
新知诞生
定理:线段垂直平分线上的点
到这条线段两个端点的距离相等.
你能写出这个定理的逆命题吗?
逆命题:到一条条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如何判断证明这个命题的真假呢?
你试试!
新知探究
已知:如图,线段AB,PA=PB.
求证:点 P在线段AB的垂直平分线上.
证明:作AB边上的中线PC.
∵PA=PB,
∴△PAB是等腰三角形
∴PC⊥AB,(三线合一)
∴PC所在直线是线段AB的垂
直平分线.
即P点在线段AB垂直平分线上
方法很多哦!
一、P点在线段AB外
C
二、P点在线段AB上
此时P点为AB中点,
P点仍在线段AB垂直平分线上.
新知诞生
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
定理:到一条条线段两个端点距离相等的点,在这条线段的垂直平分线上.
互为
逆定理
综上:线段的垂直平分线是到线段两个端点距离相等的所有点的集合.
学以致用
已知:如图,在△ABC中,AB=AC,O是△ABC内一点且OB=OC.
求证:直线AO垂直平分线段BC.
证明:
∵AB=AC,
∴点A在线段BC的垂直平分线上( ?).
∵OB=OC,
∴点A在线段BC的垂直平分线上( ?).
∴直线AO是线段BC的垂直平分线( ?).
学以致用
已知:如图,在△ABC中,AB=AC,O是△ABC内一点且OB=OC.
求证:直线AO垂直平分线段BC.
同学们想一想这题还有其他证明方法吗?想好后相互交流交流.
全等无处不在哦!
D
可证△ABO≌ACO,
再证△ABD≌ACD,
从而得证.
随堂练习
1.线段是轴对称图形吗?如果是说出它的对称轴.
是轴对称图形,
对称轴是它的垂直平分线;
还有一条对称轴是线段
本身所在直线哦!
有点坑!
2.已知:如图,AB是线段CD的垂直平分线,E、F是AB上两点.
求证:∠ECF=∠EDF.
随堂练习
方法多种,请说出你的想法!
提高练习
1.如图,在△ABC 中,BC =8,AB 的中垂线交BC于D,
AC 的中垂线交BC 与E,求△ADE 的周长.
A
B
C
D
E
解:∵D点在AB的中垂线上,
∴DA=DB.
∵E点在AC的中垂线上,
∴EA=EC.
∵S△ADE=AD+DE+AE,
∴S△ADE=DB+DE+EC=BC.
∴S△ADE=8
知识小结
线段的垂直平分线
PA=PB
点P在线段AB的垂直平分线上
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这
条线段两个端点的距离相等
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是到线段两个端点距离相等的所有点的集合
互为
逆定理
1.教材习题1.7
2.对应练习册
课后练习
又来了!
故事还在继续……
欲知后事如何,请听下回分解!
1.3线段垂直平分线
第一章 三角形的证明
第1回 线段垂直平分线的性质和判定
学习目标
1.探索证明线段垂直平分线的性质和判定.
2.能运用线段垂直平分线性质和其判定解决实际问题.
3.经历“探索-发现-猜想-证明”的过程,进一步体会证明的必要性,增强证明意识和能力,发展推理能力.
课前复习
1.等边对等角,等角对等边,逆命题,逆定理,难我不倒;
2.“三线合一”,反证法,熟能生巧;
3.不论勾股定理,还是倒过来作为判定,外加特殊全等判定(HL),小到两锐角互余,一条不会漏掉.
不论等腰还是直角,你我皆已明了!
想一想:曾经我们用折纸的办法得出“线段垂直平分线线上的点到线段两个端点距离相等”,有了前面两节证明的经验积累,你现在一定可以证明这一结论.
聪明如我的你们
一定可以搞定哦!
画图试试!
新知探究
新知探究
已知:如图,直线MN⊥AB,垂足为C,且AC=BC,P是MN上任意一点.
求证:PA=PB.
证明:∵MN⊥AB,
∴∠PCA=∠PCB=90°.
∵AC=BC,
PC=PC,
∴△PCA≌△PCB(SAS)
∴PA=PB
是不是遗漏了什么?
新知探究
已知:如图,直线MN⊥AB,垂足为C,且AC=BC,P是MN上任意一点.
求证:PA=PB.
证明:∵MN⊥AB,
∴∠PCA=∠PCB=90°.
∵AC=BC,
PC=PC,
∴△PCA≌△PCB(SAS).
∴PA=PB.
是不是遗漏了什么?
一、P点在线段AB外
二、P点在线段AB上
此时P点与C点重合,
仍满足PA =PB.
P
注意严谨哦!
新知诞生
定理:线段垂直平分线上的点
到这条线段两个端点的距离相等.
你能写出这个定理的逆命题吗?
逆命题:到一条条线段两个端点距离相等的点,在这条线段的垂直平分线上.
如何判断证明这个命题的真假呢?
你试试!
新知探究
已知:如图,线段AB,PA=PB.
求证:点 P在线段AB的垂直平分线上.
证明:作AB边上的中线PC.
∵PA=PB,
∴△PAB是等腰三角形
∴PC⊥AB,(三线合一)
∴PC所在直线是线段AB的垂
直平分线.
即P点在线段AB垂直平分线上
方法很多哦!
一、P点在线段AB外
C
二、P点在线段AB上
此时P点为AB中点,
P点仍在线段AB垂直平分线上.
新知诞生
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
定理:到一条条线段两个端点距离相等的点,在这条线段的垂直平分线上.
互为
逆定理
综上:线段的垂直平分线是到线段两个端点距离相等的所有点的集合.
学以致用
已知:如图,在△ABC中,AB=AC,O是△ABC内一点且OB=OC.
求证:直线AO垂直平分线段BC.
证明:
∵AB=AC,
∴点A在线段BC的垂直平分线上( ?).
∵OB=OC,
∴点A在线段BC的垂直平分线上( ?).
∴直线AO是线段BC的垂直平分线( ?).
学以致用
已知:如图,在△ABC中,AB=AC,O是△ABC内一点且OB=OC.
求证:直线AO垂直平分线段BC.
同学们想一想这题还有其他证明方法吗?想好后相互交流交流.
全等无处不在哦!
D
可证△ABO≌ACO,
再证△ABD≌ACD,
从而得证.
随堂练习
1.线段是轴对称图形吗?如果是说出它的对称轴.
是轴对称图形,
对称轴是它的垂直平分线;
还有一条对称轴是线段
本身所在直线哦!
有点坑!
2.已知:如图,AB是线段CD的垂直平分线,E、F是AB上两点.
求证:∠ECF=∠EDF.
随堂练习
方法多种,请说出你的想法!
提高练习
1.如图,在△ABC 中,BC =8,AB 的中垂线交BC于D,
AC 的中垂线交BC 与E,求△ADE 的周长.
A
B
C
D
E
解:∵D点在AB的中垂线上,
∴DA=DB.
∵E点在AC的中垂线上,
∴EA=EC.
∵S△ADE=AD+DE+AE,
∴S△ADE=DB+DE+EC=BC.
∴S△ADE=8
知识小结
线段的垂直平分线
PA=PB
点P在线段AB的垂直平分线上
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这
条线段两个端点的距离相等
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是到线段两个端点距离相等的所有点的集合
互为
逆定理
1.教材习题1.7
2.对应练习册
课后练习
又来了!
故事还在继续……
欲知后事如何,请听下回分解!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
