2.3等比数列概念课件(苏教版必修5)
文档属性
| 名称 | 2.3等比数列概念课件(苏教版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 396.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-25 18:26:52 | ||
图片预览






文档简介
(共15张PPT)
热 烈 欢 迎 各 位
老师光临指导!
等差数列的公差:
等差数列的通项公式:
等差数列的定义:
知识回顾:
等差数列的通项公式是如何推导
观察思考:以下几个数列有何共同特点
(1) 2,4,8,16,…
(2) 2,2 , 4, 4 …
(4) 5, 5, 5, 5, …
(3) 1, , , , …
从第 二项起,每一项与它前一项之比 等于同一常数
高一数学备课组
等比数列概念
如果一个数列从第 __项起,每一项与它的前一项的 _等于 _一个常数,那么这个数列就叫做 这个常数叫做等 数列的 _____
1.等比数列定义:
二
比
同
等比数列
公比
等差数列定义
如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差
公差通常用字母d表示
公比通常用字母q表示
比
等比数列
由于等比数列的每一项都有可能作分母,
故a 1 ≠0 且 q ≠0
等差数列
由于等差数列是作差 故a 1 d 没有要求
判断数列是等差数列的方法
判断数列是等比数列的方法
或 an+1-an=d(n≥1)
an –an-1=d(n≥2)
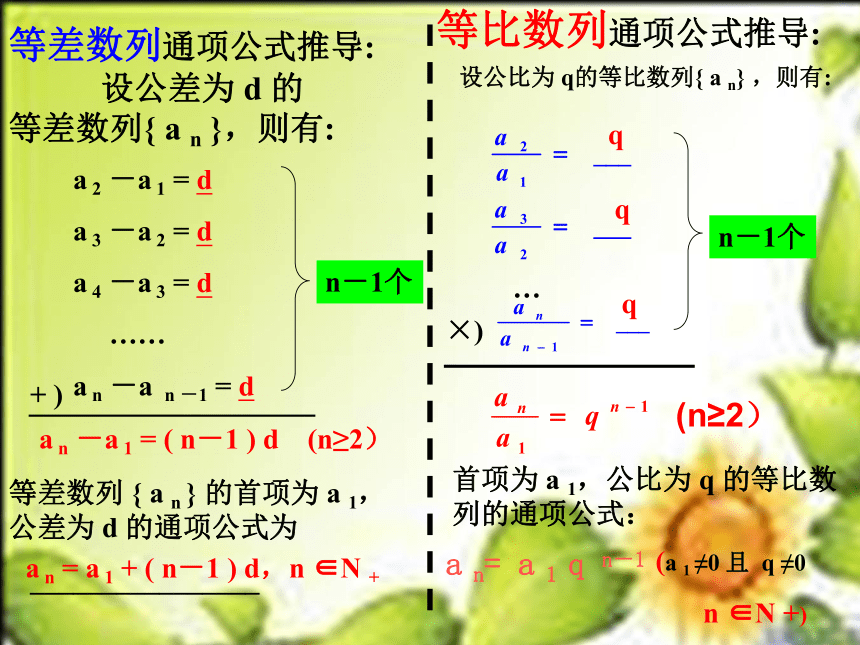
等比数列通项公式推导:
等差数列通项公式推导:
设公差为 d 的
等差数列{ a n },则有:
n-1个
a 2 -a 1 = d
a 3 -a 2 = d
a 4 -a 3 = d
……
a n -a n -1 = d
+ )
a n -a 1 = ( n-1 ) d (n≥2)
等差数列 { a n } 的首项为 a 1,公差为 d 的通项公式为
________________
a n = a 1 + ( n-1 ) d,n ∈N +
设公比为 q的等比数列{ a n} ,则有:
…
×)
n-1个
q
q
q
首项为 a 1,公比为 q 的等比数列的通项公式:
a n= a 1 q n-1
(a 1 ≠0 且 q ≠0
n ∈N +)
(n≥2)
等比数列
等差数列
常数列都是等差数列
但常数列却不一定是等比数列,
如0,0,0,0,……
等差数列通项公式:
等比数列通项公式:
首项为 a 1,公差为 d 的通项公式为
________________
a n = a 1 + ( n-1 ) d,n ∈N +
首项为 a 1,公比为 q 的 的通项公式:
a n= a 1 q n-1
(a 1 ≠0 且 q ≠0,n ∈N +)
几何意义及图象特点:
a n =
图象特点:
形如指数函数上的一些规律的点
(1) 2,4,8,16,…
(2) 2,2 , 4, 4 …
(4) 5, 5, 5, 5, …
(3) 1, , , , …
a n =2n
a n=
a n=
a n=5
判断下列数列是否为等比数列
(1)1,1,1,1,1;
(2)0,1,2,4,8;
(3)1,-1/2,1/4,-1/8,1/16;
求出下列等比数列中的未知项
(1)2,a,8;
(2)-4,b,c,1/2;
(3)d,3,27;
(1)在等比数列{an}中,
是否有an2=an-1an+1(n≥2)?
(2)如果数列{an}中,对于任意的正整数n (n≥2),都有an2=an-1an+1,那么, {an}一定是等比数列吗?
练习:课本P47页练习4,5
等比数列有没有与等差数列同样的一些性质呢
等差数列性质
(1):an=am+(n-m)d
(2)在等差数列 中若m+n=p+k,m、n、p、k∈N+则am+an=ap+aq
(3):等差中项
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
等比数列性质
(2)在等比数列 中 若m+n=p+k, m、n、p、k∈N+,则 aman=apak
(3):等比中项
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
(1):
课堂小结
(2)等比数列的通项公式及推导方法
(1)等比数列的定义
(3)等比数列的有关性质
(4)学习的思想方法:
类比方法
热 烈 欢 迎 各 位
老师光临指导!
等差数列的公差:
等差数列的通项公式:
等差数列的定义:
知识回顾:
等差数列的通项公式是如何推导
观察思考:以下几个数列有何共同特点
(1) 2,4,8,16,…
(2) 2,2 , 4, 4 …
(4) 5, 5, 5, 5, …
(3) 1, , , , …
从第 二项起,每一项与它前一项之比 等于同一常数
高一数学备课组
等比数列概念
如果一个数列从第 __项起,每一项与它的前一项的 _等于 _一个常数,那么这个数列就叫做 这个常数叫做等 数列的 _____
1.等比数列定义:
二
比
同
等比数列
公比
等差数列定义
如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差
公差通常用字母d表示
公比通常用字母q表示
比
等比数列
由于等比数列的每一项都有可能作分母,
故a 1 ≠0 且 q ≠0
等差数列
由于等差数列是作差 故a 1 d 没有要求
判断数列是等差数列的方法
判断数列是等比数列的方法
或 an+1-an=d(n≥1)
an –an-1=d(n≥2)
等比数列通项公式推导:
等差数列通项公式推导:
设公差为 d 的
等差数列{ a n },则有:
n-1个
a 2 -a 1 = d
a 3 -a 2 = d
a 4 -a 3 = d
……
a n -a n -1 = d
+ )
a n -a 1 = ( n-1 ) d (n≥2)
等差数列 { a n } 的首项为 a 1,公差为 d 的通项公式为
________________
a n = a 1 + ( n-1 ) d,n ∈N +
设公比为 q的等比数列{ a n} ,则有:
…
×)
n-1个
q
q
q
首项为 a 1,公比为 q 的等比数列的通项公式:
a n= a 1 q n-1
(a 1 ≠0 且 q ≠0
n ∈N +)
(n≥2)
等比数列
等差数列
常数列都是等差数列
但常数列却不一定是等比数列,
如0,0,0,0,……
等差数列通项公式:
等比数列通项公式:
首项为 a 1,公差为 d 的通项公式为
________________
a n = a 1 + ( n-1 ) d,n ∈N +
首项为 a 1,公比为 q 的 的通项公式:
a n= a 1 q n-1
(a 1 ≠0 且 q ≠0,n ∈N +)
几何意义及图象特点:
a n =
图象特点:
形如指数函数上的一些规律的点
(1) 2,4,8,16,…
(2) 2,2 , 4, 4 …
(4) 5, 5, 5, 5, …
(3) 1, , , , …
a n =2n
a n=
a n=
a n=5
判断下列数列是否为等比数列
(1)1,1,1,1,1;
(2)0,1,2,4,8;
(3)1,-1/2,1/4,-1/8,1/16;
求出下列等比数列中的未知项
(1)2,a,8;
(2)-4,b,c,1/2;
(3)d,3,27;
(1)在等比数列{an}中,
是否有an2=an-1an+1(n≥2)?
(2)如果数列{an}中,对于任意的正整数n (n≥2),都有an2=an-1an+1,那么, {an}一定是等比数列吗?
练习:课本P47页练习4,5
等比数列有没有与等差数列同样的一些性质呢
等差数列性质
(1):an=am+(n-m)d
(2)在等差数列 中若m+n=p+k,m、n、p、k∈N+则am+an=ap+aq
(3):等差中项
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
等比数列性质
(2)在等比数列 中 若m+n=p+k, m、n、p、k∈N+,则 aman=apak
(3):等比中项
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
(1):
课堂小结
(2)等比数列的通项公式及推导方法
(1)等比数列的定义
(3)等比数列的有关性质
(4)学习的思想方法:
类比方法
