9.2.1 总体取值规律的分析跟踪练习(含答案)
文档属性
| 名称 | 9.2.1 总体取值规律的分析跟踪练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 13:59:39 | ||
图片预览


文档简介
9.2.1 总体取值规律的分析跟踪练习
选择题
1.每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如下表所示),并根据调查结果绘制了尚不完整的统计图表(如下图)
由两个统计图表可以求得,选择D选项的人数和扇形统计图中E的圆心角度数分别为( )
A.500,28.8° B.250,28.6° C.500,28.6° D.250,28.8°
2.某单位去年的开支分布的折线图如图1所示,在这一年中的水、电、交通开支(单位:万元)如图2所示,则该单位去年的水费开支占总开支的百分比为( )
A.false B.false C.false D.false
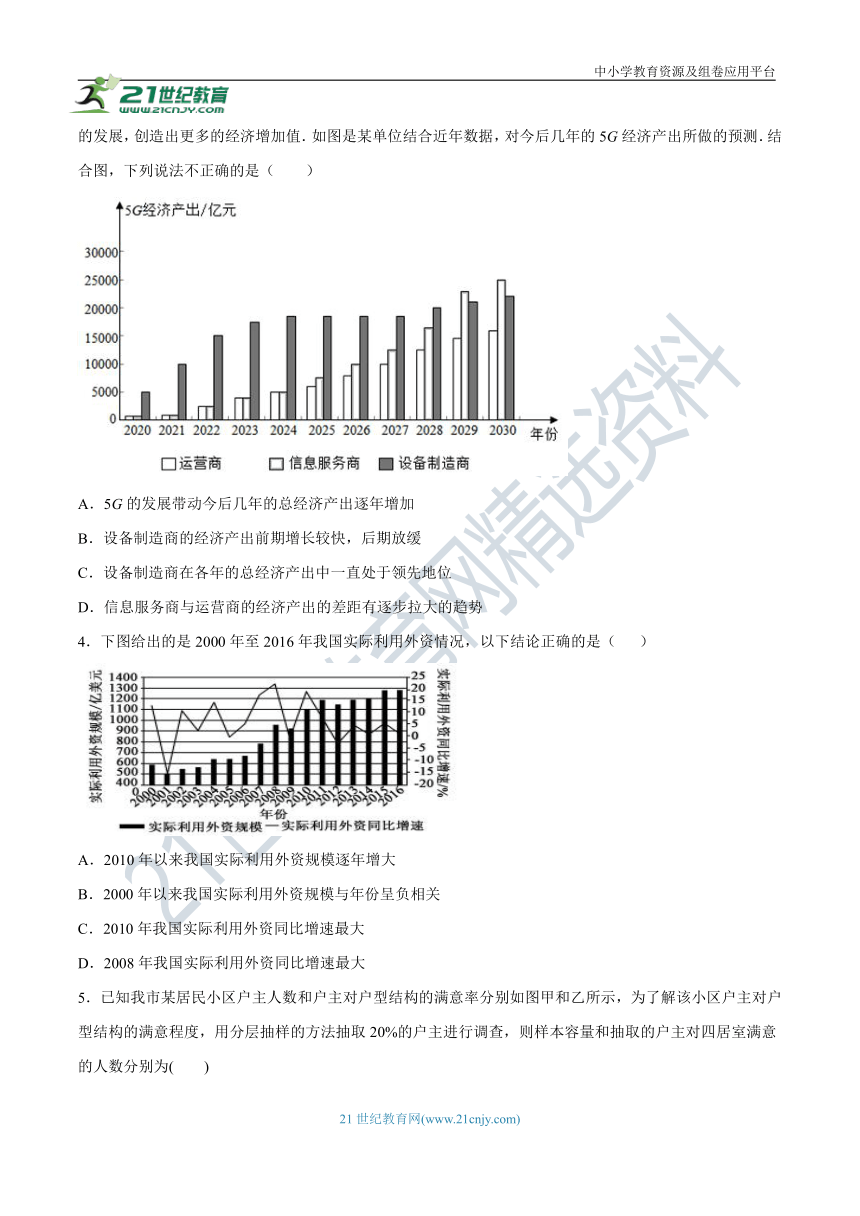
3.由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造出更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合图,下列说法不正确的是( )
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
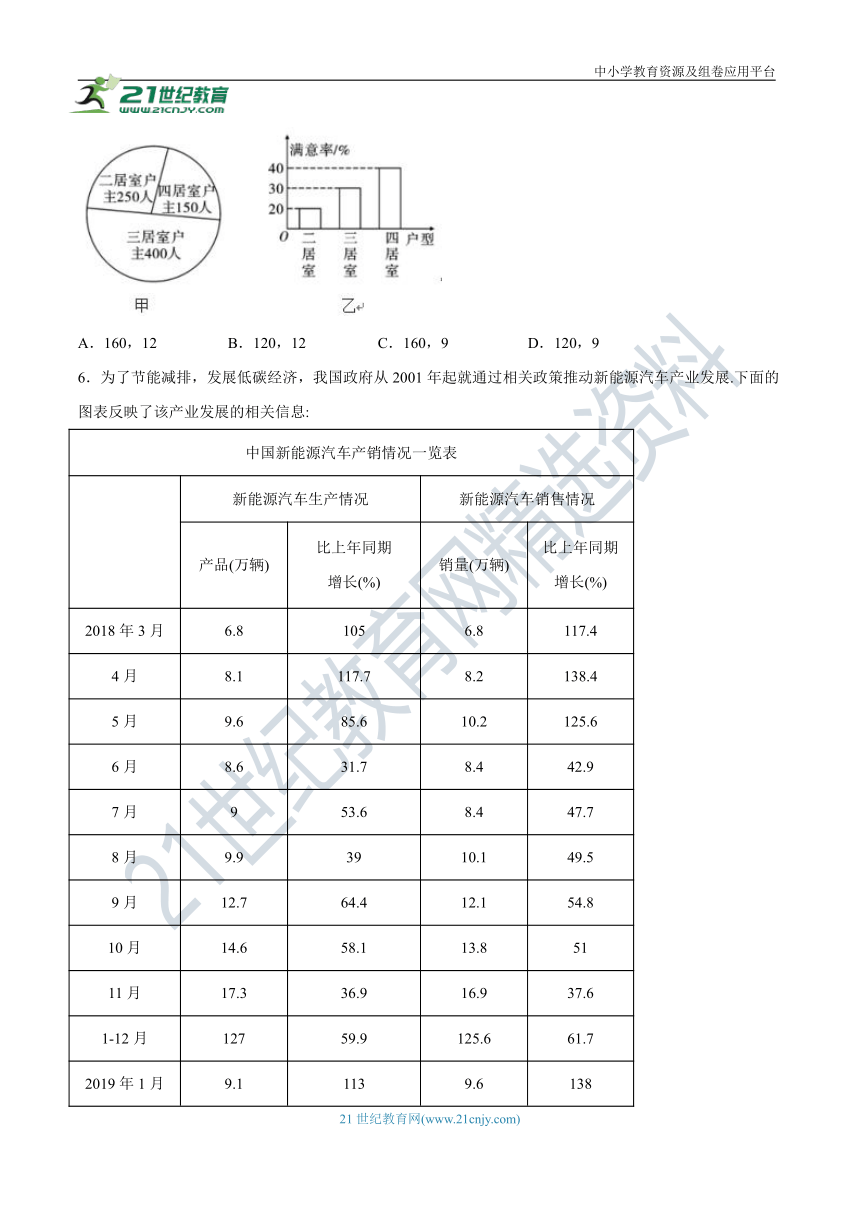
4.下图给出的是2000年至2016年我国实际利用外资情况,以下结论正确的是( )
A.2010年以来我国实际利用外资规模逐年增大
B.2000年以来我国实际利用外资规模与年份呈负相关
C.2010年我国实际利用外资同比增速最大
D.2008年我国实际利用外资同比增速最大
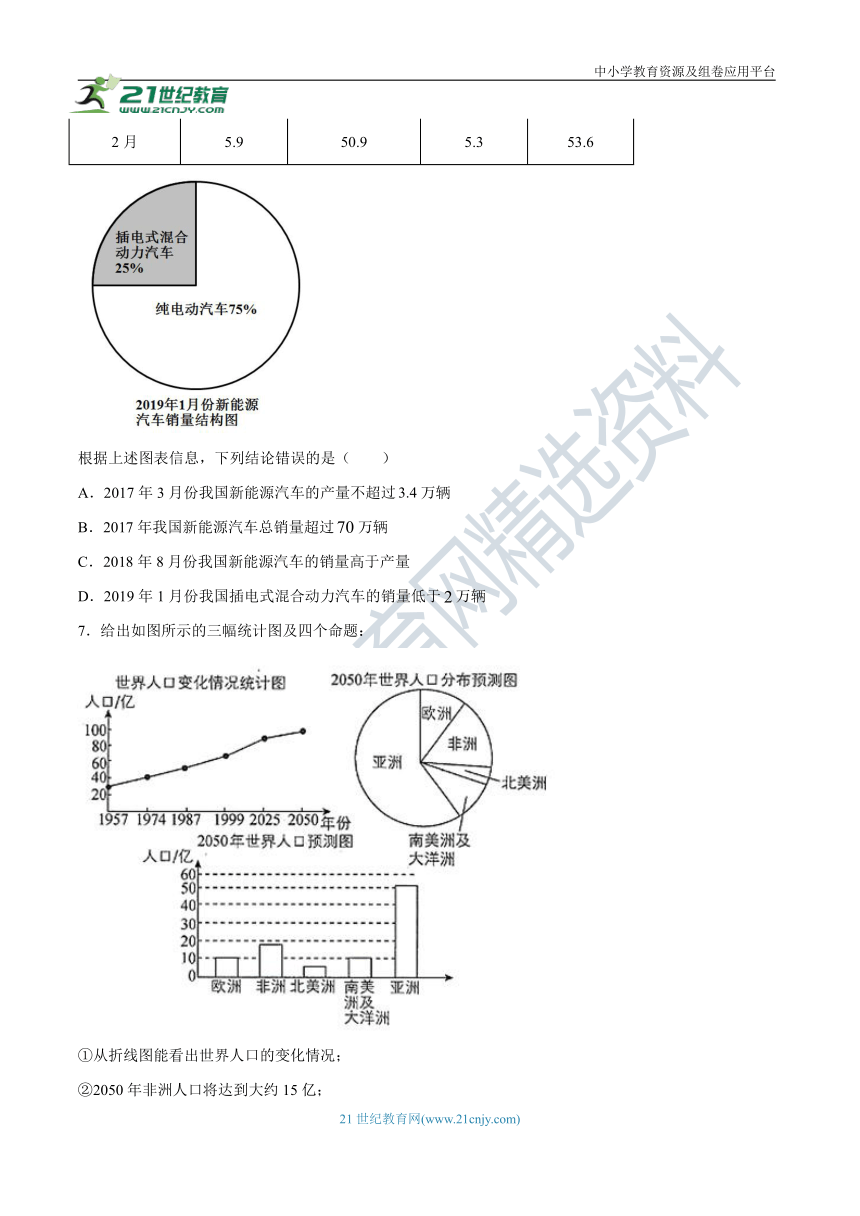
5.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图甲和乙所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
A.160,12 B.120,12 C.160,9 D.120,9
6.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表
新能源汽车生产情况
新能源汽车销售情况
产品(万辆)
比上年同期
增长(%)
销量(万辆)
比上年同期
增长(%)
2018年3月
6.8
105
6.8
117.4
4月
8.1
117.7
8.2
138.4
5月
9.6
85.6
10.2
125.6
6月
8.6
31.7
8.4
42.9
7月
9
53.6
8.4
47.7
8月
9.9
39
10.1
49.5
9月
12.7
64.4
12.1
54.8
10月
14.6
58.1
13.8
51
11月
17.3
36.9
16.9
37.6
1-12月
127
59.9
125.6
61.7
2019年1月
9.1
113
9.6
138
2月
5.9
50.9
5.3
53.6
根据上述图表信息,下列结论错误的是( )
A.2017年3月份我国新能源汽车的产量不超过false万辆
B.2017年我国新能源汽车总销量超过false万辆
C.2018年8月份我国新能源汽车的销量高于产量
D.2019年1月份我国插电式混合动力汽车的销量低于false万辆
7.给出如图所示的三幅统计图及四个命题:
①从折线图能看出世界人口的变化情况;
②2050年非洲人口将达到大约15亿;
③2050年亚洲人口比其他各洲人口的总和还要多;
④从1957年到2050年各洲中北美洲人口增长速度最慢.
其中命题正确的有( )
A.①② B.①③ C.①④ D.②④
8.已知样本数据:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,11.那么频率为0.2的是( )
A.false B.false C.false D.false
9.容量为100的某个样本数据分成10组,并填写频率分布表,若前7组频率之和为0.79,则剩下3组的频率之和为( )
A.0.21% B.0.21 C.21 D.无法确定
10.为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间false的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0 B.1 C.2 D.3
11.某高校调查了320名学生每周的自习时间(单位:小时),制成了下图所示的频率分布直方图,其中自习时间的范围是false,样本数据分组为false,false,false,false,false.根据直方图,这320名学生中每周的自习时间不足22.5小时的人数是( )
A.68 B.72 C.76 D.80
12.某学校对100间学生公寓的卫生情况进行综合评比,依考核分数分为false四个等级,其中分数在false为false等级;分数在false为false等级;分数在false为false等级;分数在false为false等级.考核评估后,得其频率分布折线图如图所示,估计这100间学生公寓评估得分的平均数是( )
A.80.25 B.80.45 C.80.5 D.80.65
解答题
13.当今的学校教育非常关注学生身体健康成长,某地安顺小学的教育行政主管部门为了了解小学生的体能情况,抽取该校二年级的部分学生进行两分钟跳绳次数测试,测试成绩分成false,false,false,false四个部分,并画出频率分布直方图如图所示,图中从左到右前三个小组的频率分别为false,false,false,且第一小组false从左向右数false的人数为5人.
false求第四小组的频率;
false求参加两分钟跳绳测试的学生人数;
false若两分钟跳绳次数不低于100次的学生体能为达标,试估计该校二年级学生体能的达标率false用百分数表示false
14.某校为调查高一、高二学生周日在家学习用时情况,随机抽取了高一、高二各false人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表(学习时间均在区间false内):
学习时间
false
false
false
false
false
false
频数
3
1
8
4
2
2
高二学生学习时间的频率分布直方图:
(1)求高二学生学习时间的频率分布直方图中的false值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
(2)利用分层抽样的方法,从高一学生学习时间在false,false的两组里随机抽取false人,再从这false人中随机抽取false人,求学习时间在false这一组中至少有false人被抽中的概率.
15.某市为制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:百度),将数据按照false,false,false分成false组,制成了如图所示的频率分布直方图:
(I)求直方图中false的值;
56789月均用电量百厦
(Ⅱ)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百度的人数,估计每户居民月均用电量的中位数,说明理由;
(Ⅲ)政府计划对月均用电量在4(百度)以下的用户进行奖励,月均用电量在false内的用户奖励20元/月,月均用电量在false内的用户奖励10元/月,月均用电量在false内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
答案
1.A 2.A 3.C 4.D 5.A 6.D 7. B 8.D 9.B 10.D 11.B 12.C
13.【答案】(1)0.2;(2)50;(3)false
【详解】false第四小组的频率为:false.
false设参加两分钟跳绳测试的学生有x人,则false,解得false,
false参加两分钟跳绳测试的学生人数为50人.
false由题意及频率分布直方图知:
样本数据参加两分钟跳绳次数测试体体能达标率为:false,
false估计该校二年级学生体能的达标率为false.
14.【答案】(1)false,3.8;(2)false
【解析】
分析:(1)根据评率分布直方图的特征各直方图的面积之和为1可得a值;(2)根据分层抽样定义可得:从高一学生学习时间在false中抽取false人,从高一学生学习时间在false中抽取false人,
然后根据古典概型计算公式可得结论.
详解:
(1)由图可知,学生学习时间在区间false内的频率为false,
false内的频率为false,所以false
设中位数为false,则false,解得false,
即该校高二学生学习时间的中位数为false.
(2)根据分层抽样,从高一学生学习时间在false中抽取false人,从高一学生学习时间在false中抽取false人,从这false人中随机抽取false人共有false种情况,其中学习时间在false这一组中没人被抽中的有false种情况,设在false这一组中至少有false人被抽中的事件为false,
则false.
15.【答案】(Ⅰ)false(Ⅱ)false(Ⅲ)false亿元
【解析】
分析:(1)利用频率分布直方图中所有小矩形的面积之和为false,可求出参数false的值;(2)根据频率分布直方图计算出200户居民月均用电量不低于6百度的频率为false,则可估计100万户居民中月均用电量不低于6百度的户数为120000,设中位数为false,由前4组频率之和为false,前5组频率之和为false,可知false,可继续计算出false的值;(3)分别计算出月均用电量在false内的用户数,可得出一年的预算.
详解:(Ⅰ)false false
(Ⅱ)200户居民月均用电量不低于6百度的频率为false,
100万户居民中月均用水量不低于6百度的户数有false;
设中位数是false百度,前false组的频率之和false
而前false组的频率之和false
所以false,false,故false.
(Ⅲ)该市月均用电量在false,false,false内的用户数分别为false,false,false,所以每月预算为false元,
故一年预算为false万元false亿元.
点睛:本题主要结合频率直方图考察样本估计总体,以及样本数字特征的计算等知识.频率分布直方图中相邻两横坐标之差表示组距,纵坐标表示false,频率false;频率分布直方图中各小长方形的面积之和为1,因此在频率分布直方图中组距是一个固定值,所以各小长方形高的比也就是频率比.
选择题
1.每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如下表所示),并根据调查结果绘制了尚不完整的统计图表(如下图)
由两个统计图表可以求得,选择D选项的人数和扇形统计图中E的圆心角度数分别为( )
A.500,28.8° B.250,28.6° C.500,28.6° D.250,28.8°
2.某单位去年的开支分布的折线图如图1所示,在这一年中的水、电、交通开支(单位:万元)如图2所示,则该单位去年的水费开支占总开支的百分比为( )
A.false B.false C.false D.false
3.由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造出更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合图,下列说法不正确的是( )
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
4.下图给出的是2000年至2016年我国实际利用外资情况,以下结论正确的是( )
A.2010年以来我国实际利用外资规模逐年增大
B.2000年以来我国实际利用外资规模与年份呈负相关
C.2010年我国实际利用外资同比增速最大
D.2008年我国实际利用外资同比增速最大
5.已知我市某居民小区户主人数和户主对户型结构的满意率分别如图甲和乙所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
A.160,12 B.120,12 C.160,9 D.120,9
6.为了节能减排,发展低碳经济,我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:
中国新能源汽车产销情况一览表
新能源汽车生产情况
新能源汽车销售情况
产品(万辆)
比上年同期
增长(%)
销量(万辆)
比上年同期
增长(%)
2018年3月
6.8
105
6.8
117.4
4月
8.1
117.7
8.2
138.4
5月
9.6
85.6
10.2
125.6
6月
8.6
31.7
8.4
42.9
7月
9
53.6
8.4
47.7
8月
9.9
39
10.1
49.5
9月
12.7
64.4
12.1
54.8
10月
14.6
58.1
13.8
51
11月
17.3
36.9
16.9
37.6
1-12月
127
59.9
125.6
61.7
2019年1月
9.1
113
9.6
138
2月
5.9
50.9
5.3
53.6
根据上述图表信息,下列结论错误的是( )
A.2017年3月份我国新能源汽车的产量不超过false万辆
B.2017年我国新能源汽车总销量超过false万辆
C.2018年8月份我国新能源汽车的销量高于产量
D.2019年1月份我国插电式混合动力汽车的销量低于false万辆
7.给出如图所示的三幅统计图及四个命题:
①从折线图能看出世界人口的变化情况;
②2050年非洲人口将达到大约15亿;
③2050年亚洲人口比其他各洲人口的总和还要多;
④从1957年到2050年各洲中北美洲人口增长速度最慢.
其中命题正确的有( )
A.①② B.①③ C.①④ D.②④
8.已知样本数据:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,11.那么频率为0.2的是( )
A.false B.false C.false D.false
9.容量为100的某个样本数据分成10组,并填写频率分布表,若前7组频率之和为0.79,则剩下3组的频率之和为( )
A.0.21% B.0.21 C.21 D.无法确定
10.为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
①样本数据落在区间false的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0 B.1 C.2 D.3
11.某高校调查了320名学生每周的自习时间(单位:小时),制成了下图所示的频率分布直方图,其中自习时间的范围是false,样本数据分组为false,false,false,false,false.根据直方图,这320名学生中每周的自习时间不足22.5小时的人数是( )
A.68 B.72 C.76 D.80
12.某学校对100间学生公寓的卫生情况进行综合评比,依考核分数分为false四个等级,其中分数在false为false等级;分数在false为false等级;分数在false为false等级;分数在false为false等级.考核评估后,得其频率分布折线图如图所示,估计这100间学生公寓评估得分的平均数是( )
A.80.25 B.80.45 C.80.5 D.80.65
解答题
13.当今的学校教育非常关注学生身体健康成长,某地安顺小学的教育行政主管部门为了了解小学生的体能情况,抽取该校二年级的部分学生进行两分钟跳绳次数测试,测试成绩分成false,false,false,false四个部分,并画出频率分布直方图如图所示,图中从左到右前三个小组的频率分别为false,false,false,且第一小组false从左向右数false的人数为5人.
false求第四小组的频率;
false求参加两分钟跳绳测试的学生人数;
false若两分钟跳绳次数不低于100次的学生体能为达标,试估计该校二年级学生体能的达标率false用百分数表示false
14.某校为调查高一、高二学生周日在家学习用时情况,随机抽取了高一、高二各false人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表(学习时间均在区间false内):
学习时间
false
false
false
false
false
false
频数
3
1
8
4
2
2
高二学生学习时间的频率分布直方图:
(1)求高二学生学习时间的频率分布直方图中的false值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
(2)利用分层抽样的方法,从高一学生学习时间在false,false的两组里随机抽取false人,再从这false人中随机抽取false人,求学习时间在false这一组中至少有false人被抽中的概率.
15.某市为制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:百度),将数据按照false,false,false分成false组,制成了如图所示的频率分布直方图:
(I)求直方图中false的值;
56789月均用电量百厦
(Ⅱ)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百度的人数,估计每户居民月均用电量的中位数,说明理由;
(Ⅲ)政府计划对月均用电量在4(百度)以下的用户进行奖励,月均用电量在false内的用户奖励20元/月,月均用电量在false内的用户奖励10元/月,月均用电量在false内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
答案
1.A 2.A 3.C 4.D 5.A 6.D 7. B 8.D 9.B 10.D 11.B 12.C
13.【答案】(1)0.2;(2)50;(3)false
【详解】false第四小组的频率为:false.
false设参加两分钟跳绳测试的学生有x人,则false,解得false,
false参加两分钟跳绳测试的学生人数为50人.
false由题意及频率分布直方图知:
样本数据参加两分钟跳绳次数测试体体能达标率为:false,
false估计该校二年级学生体能的达标率为false.
14.【答案】(1)false,3.8;(2)false
【解析】
分析:(1)根据评率分布直方图的特征各直方图的面积之和为1可得a值;(2)根据分层抽样定义可得:从高一学生学习时间在false中抽取false人,从高一学生学习时间在false中抽取false人,
然后根据古典概型计算公式可得结论.
详解:
(1)由图可知,学生学习时间在区间false内的频率为false,
false内的频率为false,所以false
设中位数为false,则false,解得false,
即该校高二学生学习时间的中位数为false.
(2)根据分层抽样,从高一学生学习时间在false中抽取false人,从高一学生学习时间在false中抽取false人,从这false人中随机抽取false人共有false种情况,其中学习时间在false这一组中没人被抽中的有false种情况,设在false这一组中至少有false人被抽中的事件为false,
则false.
15.【答案】(Ⅰ)false(Ⅱ)false(Ⅲ)false亿元
【解析】
分析:(1)利用频率分布直方图中所有小矩形的面积之和为false,可求出参数false的值;(2)根据频率分布直方图计算出200户居民月均用电量不低于6百度的频率为false,则可估计100万户居民中月均用电量不低于6百度的户数为120000,设中位数为false,由前4组频率之和为false,前5组频率之和为false,可知false,可继续计算出false的值;(3)分别计算出月均用电量在false内的用户数,可得出一年的预算.
详解:(Ⅰ)false false
(Ⅱ)200户居民月均用电量不低于6百度的频率为false,
100万户居民中月均用水量不低于6百度的户数有false;
设中位数是false百度,前false组的频率之和false
而前false组的频率之和false
所以false,false,故false.
(Ⅲ)该市月均用电量在false,false,false内的用户数分别为false,false,false,所以每月预算为false元,
故一年预算为false万元false亿元.
点睛:本题主要结合频率直方图考察样本估计总体,以及样本数字特征的计算等知识.频率分布直方图中相邻两横坐标之差表示组距,纵坐标表示false,频率false;频率分布直方图中各小长方形的面积之和为1,因此在频率分布直方图中组距是一个固定值,所以各小长方形高的比也就是频率比.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
