高考数学模拟题以及答案(三角函数与立体几何)
文档属性
| 名称 | 高考数学模拟题以及答案(三角函数与立体几何) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-26 00:00:00 | ||
图片预览


文档简介
高考数学模拟题(三角函数和立体几何)
三角函数
1.在△ABC中,角A、B、C所对的边分别为a、b、c,若(2bc)cosA=acosC,则角A=
2.计算:sin20100 =
3.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为和,第一排和最后一排的距离为米,旗杆底部 旗手应以 ▲ (米 /秒)的速度匀速升旗.
4.在ABC中,内角A,B,C的对边分别为,b,c,,
且满足sinB+ cosB =, a= 1
(I)求角B的大小;
(II)若b是a和c的等比中项,求ABC的面积.
5.已知函数f(x)=
(1)求f(x)的最大值及此时x的值
(2)求f(1)+f(2)+f(3)+…+f(2009)的值
6.已知向量函数
.
(1)求函数的最小正周期;
(2)将函数的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移 个单位得到的图象,试探讨:当时,函数与的图象的交点个数.
7.在中,分别是角A、B、C的对边,,且
(1)求角A的大小;
(2)记,作出函数的图象。
立体几何
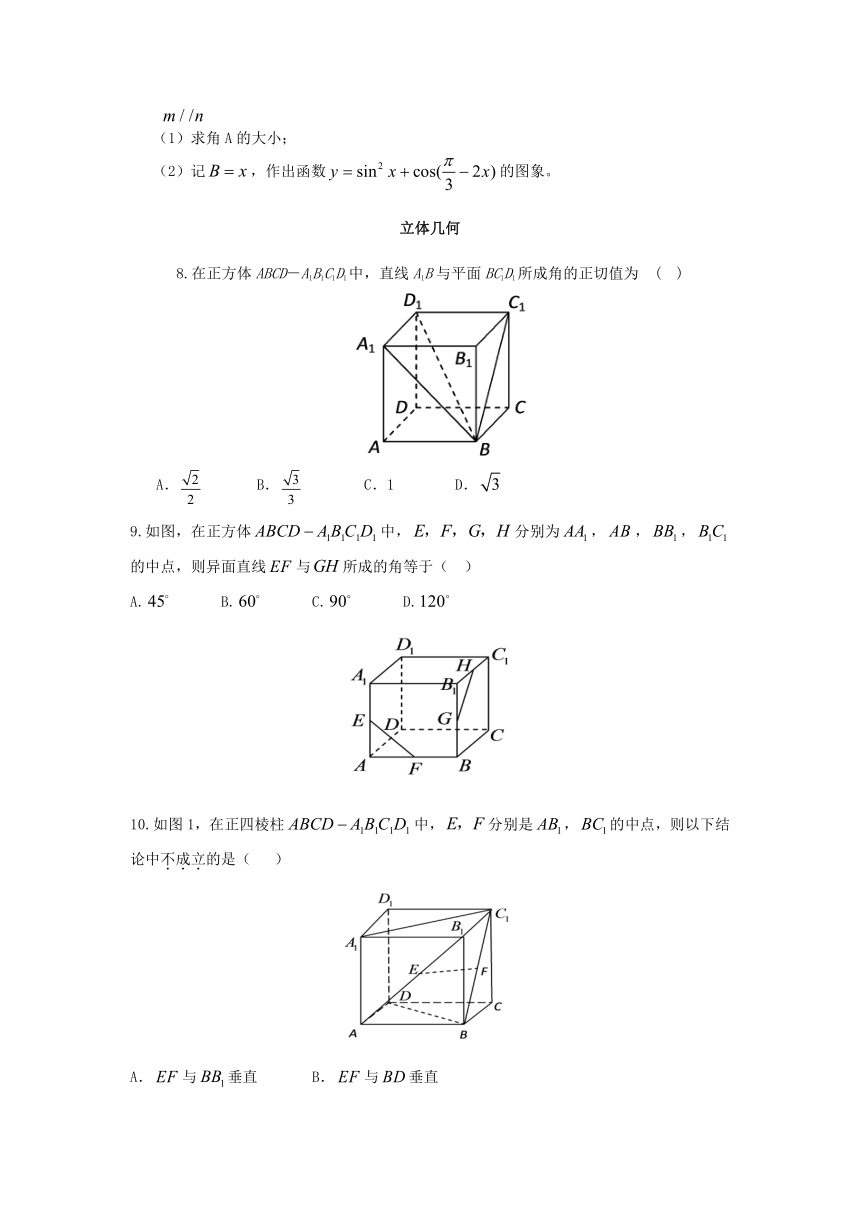
8.在正方体ABCD-A1B1C1D1中,直线A1B与平面BC1D1所成角的正切值为 ( )
A. B. C.1 D.
9.如图,在正方体中,分别为,,,的中点,则异面直线与所成的角等于( )
A. B. C. D.
10.如图1,在正四棱柱中,分别是,的中点,则以下结论中不成立的是( )
A.与垂直 B.与垂直
C.与异面 D.与异面
11.如图,正方体的棱线长为1,线段上有两个动点E,F,且③,则下列结论中错误的是 ( )
A. B.
C.三棱锥的体积为定值
D.
12.给定下列四个命题:
①若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
13.函数的图象恒过定点,若点在直线上,则的最小值为 .
14.如图,在直四棱柱中,
已知,.
(1)求证:;
(2)设是上一点,试确定的位置,使平面
,并说明理由.
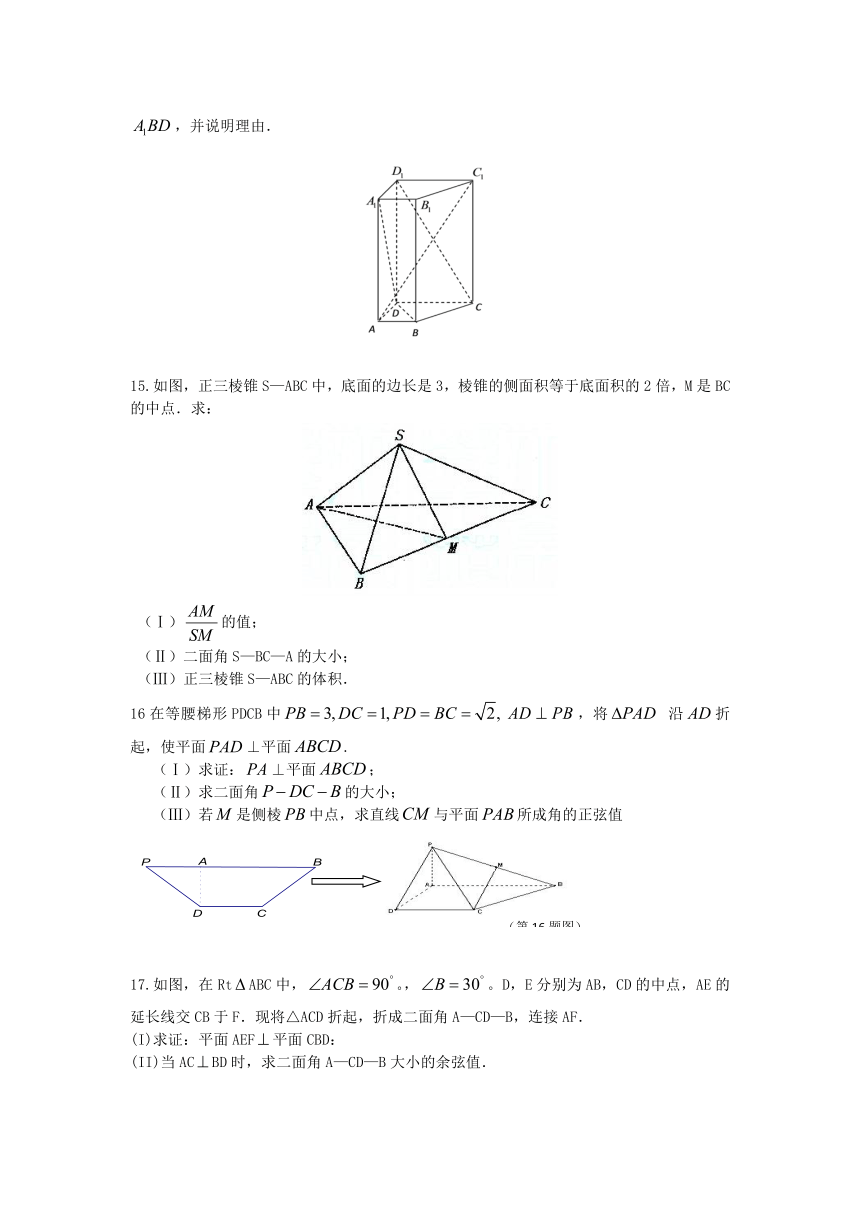
15.如图,正三棱锥S—ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.求:
(Ⅰ)的值;
(Ⅱ)二面角S—BC—A的大小;
(Ⅲ)正三棱锥S—ABC的体积.
16在等腰梯形PDCB中,将 沿折起,使平面⊥平面.
(Ⅰ)求证:⊥平面;
(Ⅱ)求二面角的大小;
(Ⅲ)若是侧棱中点,求直线与平面所成角的正弦值
17.如图,在RtABC中,。,。D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD折起,折成二面角A—CD—B,连接AF.
(I)求证:平面AEF平面CBD:
(II)当ACBD时,求二面角A—CD—B大小的余弦值.
三视图
18.下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是
A.①② B.②③ C.②④ D.①③
19.一个多面体的三视图分别是正方形、等腰三角形和矩形,
其尺寸如图,则该多面体的体积为
(A) (B) (C) (D)
20.某个几何体的三视图如图所示,则该几何体的体积是( )
A. B.
C. D.
21.一空间几何体的三视图如图所示,则该几何体的体积为( ).
A. B.
C. D.
22.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是( )
A. B.
C. D.
高考数学模拟题(三角函数和立体几何)
答案
1.
2 . -0.5
3. 0.6
4. B= S=
5.(1)
∴时, (2)原式=
6.(1)
(2)可得所以时,2个交点;时,1个交点; 时,没有交点.
7.(1)由 ( http: / / www. / )得 ( http: / / www. / ),
由正弦定理得 ( http: / / www. / ),
( http: / / www. / ) ( http: / / www. / ) ,
( http: / / www. / ) ( http: / / www. / ) ,
( http: / / www. / ) .
(第18题)
(2)化简得:, ,
8.B 9.B 10.D 11.D 12.D 13.4 14.(2).中点
15. 解析:(Ⅰ)∵SB=SC,AB=AC,M为BC中点,
∴SM⊥BC,AM⊥BC. (2分)
由棱锥的侧面积等于底面积的2倍,即
得.
(Ⅱ)作正三棱锥的高SG,则G为正三角形ABC的中心,G在AM上,
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S—BC—A的平面角.(6分)
在Rt△SGM中,∵∴∠SMA=∠SMG=60°,
即二面角S—BC—A的大小为60°.
(Ⅲ)∵△ABC的边长是3,
∴,
∴.
评析计算二面角大小,既可以根据二面角的定义,通过作出二面角的平面角,再解三角形求角,也可以运用向量方法,转化为计算两个平面的法向量的夹角.做题时要考虑前后联系,注意选择简便的方法.
16.(Ⅰ)在梯形中,
又
⊥平面
(Ⅱ)由(Ⅰ)得:⊥平面
又
就是二面角的平面角
在中,
即二面角的大小为
(Ⅲ)作交于点,连
⊥平面
17. tan=
18.C 19.A 20.B 21.C 22.D
(第3题图)
(第16题图)
俯视图
正(主)视图
侧(左)视图
2
3
2
2
三角函数
1.在△ABC中,角A、B、C所对的边分别为a、b、c,若(2bc)cosA=acosC,则角A=
2.计算:sin20100 =
3.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为和,第一排和最后一排的距离为米,旗杆底部 旗手应以 ▲ (米 /秒)的速度匀速升旗.
4.在ABC中,内角A,B,C的对边分别为,b,c,,
且满足sinB+ cosB =, a= 1
(I)求角B的大小;
(II)若b是a和c的等比中项,求ABC的面积.
5.已知函数f(x)=
(1)求f(x)的最大值及此时x的值
(2)求f(1)+f(2)+f(3)+…+f(2009)的值
6.已知向量函数
.
(1)求函数的最小正周期;
(2)将函数的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移 个单位得到的图象,试探讨:当时,函数与的图象的交点个数.
7.在中,分别是角A、B、C的对边,,且
(1)求角A的大小;
(2)记,作出函数的图象。
立体几何
8.在正方体ABCD-A1B1C1D1中,直线A1B与平面BC1D1所成角的正切值为 ( )
A. B. C.1 D.
9.如图,在正方体中,分别为,,,的中点,则异面直线与所成的角等于( )
A. B. C. D.
10.如图1,在正四棱柱中,分别是,的中点,则以下结论中不成立的是( )
A.与垂直 B.与垂直
C.与异面 D.与异面
11.如图,正方体的棱线长为1,线段上有两个动点E,F,且③,则下列结论中错误的是 ( )
A. B.
C.三棱锥的体积为定值
D.
12.给定下列四个命题:
①若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
13.函数的图象恒过定点,若点在直线上,则的最小值为 .
14.如图,在直四棱柱中,
已知,.
(1)求证:;
(2)设是上一点,试确定的位置,使平面
,并说明理由.
15.如图,正三棱锥S—ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.求:
(Ⅰ)的值;
(Ⅱ)二面角S—BC—A的大小;
(Ⅲ)正三棱锥S—ABC的体积.
16在等腰梯形PDCB中,将 沿折起,使平面⊥平面.
(Ⅰ)求证:⊥平面;
(Ⅱ)求二面角的大小;
(Ⅲ)若是侧棱中点,求直线与平面所成角的正弦值
17.如图,在RtABC中,。,。D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD折起,折成二面角A—CD—B,连接AF.
(I)求证:平面AEF平面CBD:
(II)当ACBD时,求二面角A—CD—B大小的余弦值.
三视图
18.下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是
A.①② B.②③ C.②④ D.①③
19.一个多面体的三视图分别是正方形、等腰三角形和矩形,
其尺寸如图,则该多面体的体积为
(A) (B) (C) (D)
20.某个几何体的三视图如图所示,则该几何体的体积是( )
A. B.
C. D.
21.一空间几何体的三视图如图所示,则该几何体的体积为( ).
A. B.
C. D.
22.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是( )
A. B.
C. D.
高考数学模拟题(三角函数和立体几何)
答案
1.
2 . -0.5
3. 0.6
4. B= S=
5.(1)
∴时, (2)原式=
6.(1)
(2)可得所以时,2个交点;时,1个交点; 时,没有交点.
7.(1)由 ( http: / / www. / )得 ( http: / / www. / ),
由正弦定理得 ( http: / / www. / ),
( http: / / www. / ) ( http: / / www. / ) ,
( http: / / www. / ) ( http: / / www. / ) ,
( http: / / www. / ) .
(第18题)
(2)化简得:, ,
8.B 9.B 10.D 11.D 12.D 13.4 14.(2).中点
15. 解析:(Ⅰ)∵SB=SC,AB=AC,M为BC中点,
∴SM⊥BC,AM⊥BC. (2分)
由棱锥的侧面积等于底面积的2倍,即
得.
(Ⅱ)作正三棱锥的高SG,则G为正三角形ABC的中心,G在AM上,
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S—BC—A的平面角.(6分)
在Rt△SGM中,∵∴∠SMA=∠SMG=60°,
即二面角S—BC—A的大小为60°.
(Ⅲ)∵△ABC的边长是3,
∴,
∴.
评析计算二面角大小,既可以根据二面角的定义,通过作出二面角的平面角,再解三角形求角,也可以运用向量方法,转化为计算两个平面的法向量的夹角.做题时要考虑前后联系,注意选择简便的方法.
16.(Ⅰ)在梯形中,
又
⊥平面
(Ⅱ)由(Ⅰ)得:⊥平面
又
就是二面角的平面角
在中,
即二面角的大小为
(Ⅲ)作交于点,连
⊥平面
17. tan=
18.C 19.A 20.B 21.C 22.D
(第3题图)
(第16题图)
俯视图
正(主)视图
侧(左)视图
2
3
2
2
