四年级数学下册课件-5.3 三角形内角和 -人教版(共23张PPT)
文档属性
| 名称 | 四年级数学下册课件-5.3 三角形内角和 -人教版(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 46.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 13:36:40 | ||
图片预览




文档简介
三角形内角和
三角形内角和
形状似座山,稳定性能坚;
三竿首尾连,学问不简单。
猜 谜 语
(猜一种几何图形)
3
1
2
∠1+∠2+∠3
观 察
锐角三角形
直角三角形
钝角三角形
1
2
3
1
1
2
2
3
3
所有三角形的内角和都是180°吗?
小组合作要求:
每组选择一个三角形。
准备汇报。(我选了什么三角形?我是怎样测量的?结论是什么?)
用量角器测量你们小组内的三角形每个内角的度数,并计算出内角和,记录在表格里。
3
1
2
∠1
∠2
∠3
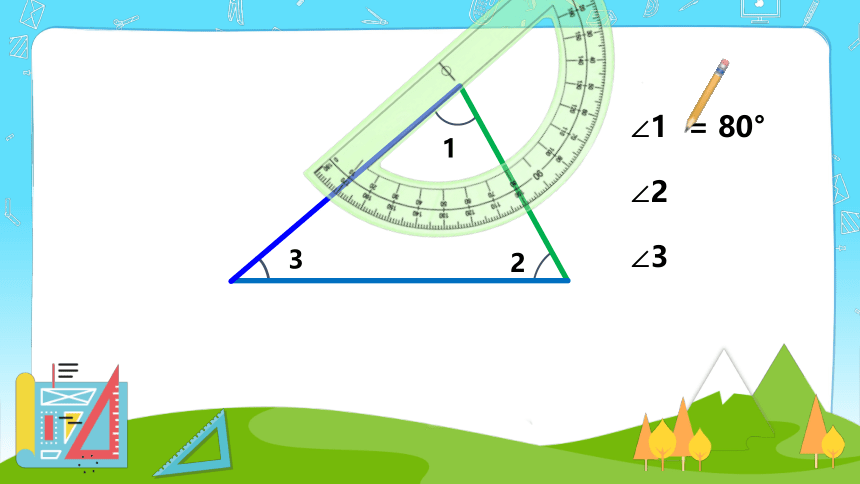
= 80°
= 60°
= 40°
3
1
2
∠1
∠2
∠3
= 80°
3
1
2
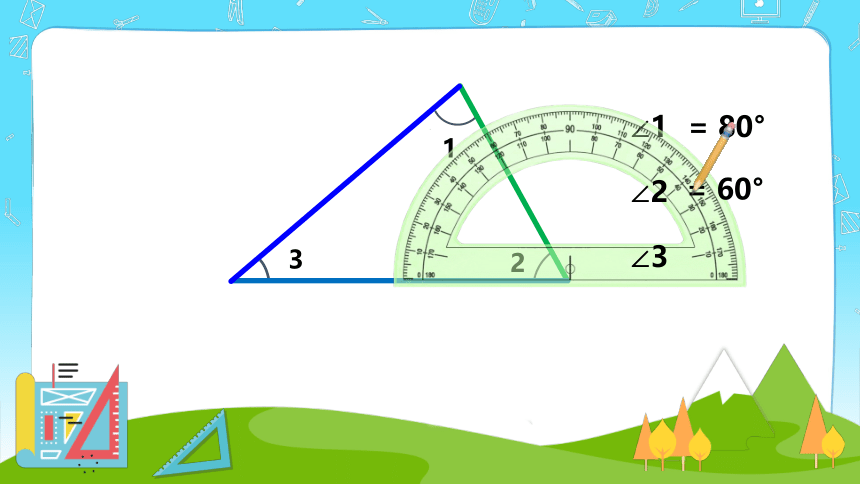
∠1
∠2
∠3
= 80°
= 60°
3
1
2
∠1
∠2
∠3
= 80°
= 60°
= 40°
∠1+∠2+∠3=80°+60°+40°=180°
活动记录表
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}
内角
度数
三角形
∠1
∠2
∠3
内角和
锐角三角形
直角三角形
钝角三角形
我的发现
合作探究
每个小组选任两种三角形进行研究。
动手操作,把你们组好的想法展示在表格的相应位置。
把我的发现填完整。
2
1
3
2
1
3
1
2
3
3
1
2
3
1
2
1
1
剪&拼
3
2
1
平角:1800
平角:1800
1
平角:1800
2
2
3
钝角三角形
1
1
3
锐角三角形
1
2
3
直角三角形
3
1
2
1
3
2
1
3
2
早在300多年前这位法国的科学家就已经发现了任何三角形的内角和是180度,而他当时才12岁。
法国数学家,物理学家,近代概率论的奠基者
帕斯卡
数学文化
内角和:4×90°=360°
数学文化
帕斯卡是怎么证明的呢?
沿对角线分为两个相同的直角三角形
直角三角形的内角和
360°÷2=180°
长方形的四个角是直角
90°
90°
90°
90°
帕斯卡是怎么证明的呢?
沿对角线分为两个相同的直角三角形
内角和:4×90°=360°
长方形的四个角是直角
直角三角形的内角和
360°÷ 2 = 180°
数学文化
任何三角形的内角和都是180°
计算三角形中被笑脸遮盖角的度数。
80°
30°
70°
40°
20°
120°
180°-40°-20°=
180°- 80°- 30°=
70°
120°
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
180°- 70°- 70°=
40°
答:每个小三角形的内角和仍是180 °
把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
两个直角三角形的和:180°+ 180°=360°
三角形的内角和:360°-90°-90°=180°
根据所学的知识,你能想办法求出下面图形的内角和吗?
拓展应用:
6
7
8
111
毕达哥拉斯
名人名言
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。
三角形内角和
形状似座山,稳定性能坚;
三竿首尾连,学问不简单。
猜 谜 语
(猜一种几何图形)
3
1
2
∠1+∠2+∠3
观 察
锐角三角形
直角三角形
钝角三角形
1
2
3
1
1
2
2
3
3
所有三角形的内角和都是180°吗?
小组合作要求:
每组选择一个三角形。
准备汇报。(我选了什么三角形?我是怎样测量的?结论是什么?)
用量角器测量你们小组内的三角形每个内角的度数,并计算出内角和,记录在表格里。
3
1
2
∠1
∠2
∠3
= 80°
= 60°
= 40°
3
1
2
∠1
∠2
∠3
= 80°
3
1
2
∠1
∠2
∠3
= 80°
= 60°
3
1
2
∠1
∠2
∠3
= 80°
= 60°
= 40°
∠1+∠2+∠3=80°+60°+40°=180°
活动记录表
{E8B1032C-EA38-4F05-BA0D-38AFFFC7BED3}
内角
度数
三角形
∠1
∠2
∠3
内角和
锐角三角形
直角三角形
钝角三角形
我的发现
合作探究
每个小组选任两种三角形进行研究。
动手操作,把你们组好的想法展示在表格的相应位置。
把我的发现填完整。
2
1
3
2
1
3
1
2
3
3
1
2
3
1
2
1
1
剪&拼
3
2
1
平角:1800
平角:1800
1
平角:1800
2
2
3
钝角三角形
1
1
3
锐角三角形
1
2
3
直角三角形
3
1
2
1
3
2
1
3
2
早在300多年前这位法国的科学家就已经发现了任何三角形的内角和是180度,而他当时才12岁。
法国数学家,物理学家,近代概率论的奠基者
帕斯卡
数学文化
内角和:4×90°=360°
数学文化
帕斯卡是怎么证明的呢?
沿对角线分为两个相同的直角三角形
直角三角形的内角和
360°÷2=180°
长方形的四个角是直角
90°
90°
90°
90°
帕斯卡是怎么证明的呢?
沿对角线分为两个相同的直角三角形
内角和:4×90°=360°
长方形的四个角是直角
直角三角形的内角和
360°÷ 2 = 180°
数学文化
任何三角形的内角和都是180°
计算三角形中被笑脸遮盖角的度数。
80°
30°
70°
40°
20°
120°
180°-40°-20°=
180°- 80°- 30°=
70°
120°
一个等腰三角形的风筝,它的一个底角是700,它的顶角是多少度?
180°- 70°- 70°=
40°
答:每个小三角形的内角和仍是180 °
把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
两个直角三角形的和:180°+ 180°=360°
三角形的内角和:360°-90°-90°=180°
根据所学的知识,你能想办法求出下面图形的内角和吗?
拓展应用:
6
7
8
111
毕达哥拉斯
名人名言
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。
