2020-2021学年北师大版八年级下册第三章图形的平移与旋转复习课课件(共17张)
文档属性
| 名称 | 2020-2021学年北师大版八年级下册第三章图形的平移与旋转复习课课件(共17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 775.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 18:20:05 | ||
图片预览





文档简介
图形的平移与旋转
复习课
练习检测 知识梳理
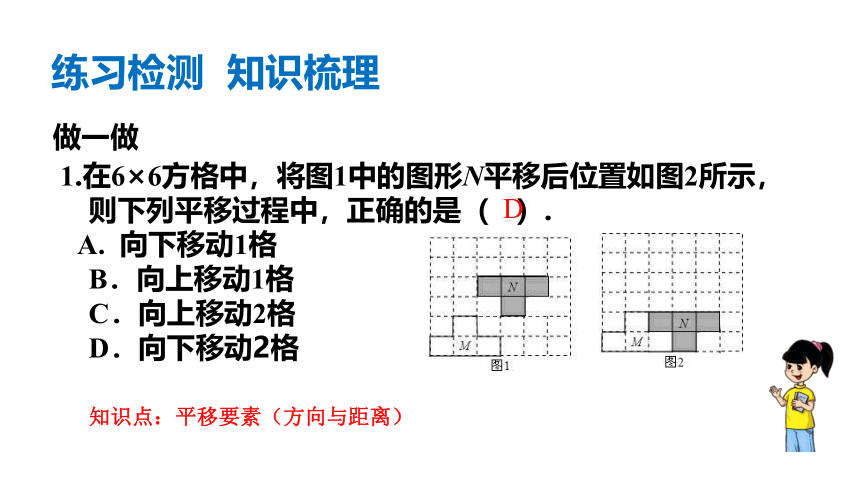
1.在6×6方格中,将图1中的图形N平移后位置如图2所示,
则下列平移过程中,正确的是( ).
A. 向下移动1格
B.向上移动1格
C.向上移动2格
D.向下移动2格
D
知识点:平移要素(方向与距离)
做一做
2. 将点A(1,-3)向右平移2个单位,再向下平移2个单位后
得到点B(a,b),则 ab= .
练习检测 知识梳理
知识点:
平移坐标有特征,
横坐标左减右加,
纵坐标上加下减.
-15
平移——定义及性质
1. 在平面内,将一个图形沿某个 移动一定的 ,这样
的图形移动称为平移.
2. 平移的性质:
(1)对应线段平行(或共线)且 ,对应点所连的线段 ,
图形上的每个点都沿同一个方向移动了相同的距离;
(2)对应角分别 ,且对应角的两边分别平行、方向一致;
(3)平移变换后的图形与原图形 .
方向
距离
相等
相等
相等
全等
填一填
练习检测 知识梳理
做一做
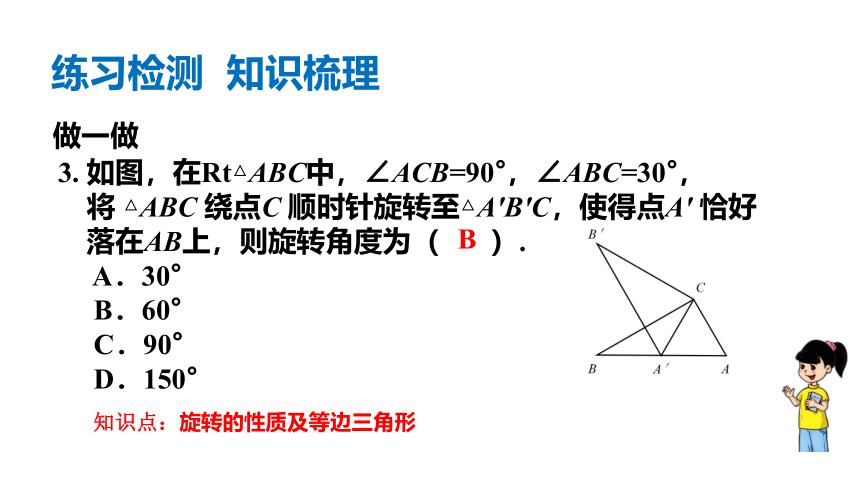
3. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,
将 △ABC 绕点C 顺时针旋转至△A′B′C,使得点A′ 恰好
落在AB上,则旋转角度为( ).
A.30°
B.60°
C.90°
D.150°
B
知识点:旋转的性质及等边三角形
练习检测 知识梳理
4. 如图,Rt△OAB的直角边 OA 在y轴上,点 B 在第一象限内,
OA=2,AB=1,若将△OAB 绕点 O 按顺时针方向旋转90°,
则点B的对应点的坐标是 .
(2,-1)
知识点:旋转性质,长度与坐标
旋转——定义及性质
1. 定义:在平面内,把一个图形绕着某一个定点沿着某个
方向旋转一定的角度,这样的图形运动称为旋转.这个
定点叫做 ,转动的角叫做 .
2. 图形的旋转有三个基本条件
(1) ;(2) ;(3) .
3. 旋转的性质:
(1)对应点到旋转中心的距离 ;
(2)对应点与旋转中心所连线段的夹角等于 ;
(3)旋转前后的图形 .
旋转中心
旋转角
旋转中心
旋转方向
旋转角
相等
旋转角
全等
填一填
练习检测 知识梳理
5. 正方形ABCD在直角坐标系中的位置如图所示,将正方形
ABCD绕点A顺时针方向旋转180°后,C点的坐标是 .
解析:AB=2,则正方形ABCD绕点A顺时针方向
旋转180°后C的对应点设是,C点的坐标是C′,
则AC′=AC=2,OC′=OA+AC′=3,
故坐标是(3,0).
做一做
(3,0)
中心对称与中心对称图形——区别与联系
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系,中心对
称图形指一个图形本身成中心对称.
联系: 如果将成中心对称的两个图形看成一个整体,则它
们是中心对称图形.如果将中心对称图形对称的部
分看成两个图形,则它们成中心对称.
练习检测 知识梳理
简单的图案设计
(1)确定“基本图案”;
(2)分析轴对称、平移、旋转等变换手法及组合的合理运用.
知识构建
图形的平移与旋转
图形的平移
图形的旋转
中心对称
简单的图案设计
两个图形成中心对称
中心对称图形
拓展提升
6. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC
沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接
A′C,求△A′B′C的周长.
思路:60°的理解、平移的性质
解:由题意可得B′C′=BC,CC′=2,
∴B′C=4,
又∠B=60°,∴△A′B′C为等边三角形,
∴△A′B′C的周长为4×3=12.
拓展提升
7. 如图,在长20m,宽10m的长方形草地内修建了宽2m的
道路,则草地的面积为 m2.
144
思路:将图中道路分别向左、右上平移,
得到右图,此时草地部分的长为
20-2=18m,宽为10-2=8m,
则草地面积为18×8=144m2.
拓展提升
8. 在直角坐标系中的矩形OABC,OA=4,OC=2,将矩形
OABC绕点C逆时针旋转至矩形DEFC,DE经过点B.
求旋转角的大小.
y
x
A
F
D
C
B
o
E
提示:如何理解DE经过点B,特殊角度的
直角三角形及旋转性质
解析:根据OA=4,OC=2,BC=OA,
而由BC=2CD,可以求出∠BCD=60°,
则可得旋转角为30°.
拓展提升
9. 如图,已知△ABC中,∠C=90°, AC=BC= ,将△ABC
绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,
判断BC′与AB′的位置关系并说明理由?
提示:连结BB′,并延长BC′交AB′于点D,
利用三角形全等
解析:如图,连接BB′,
∵△ABC绕点A顺时针方向旋转60°
得到△AB′C′,∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,∴AB=BB′,
再证△ABD′≌△B′BD,即可得BC′⊥AB′.
课堂总结
思考本章的知识框架?
回顾并分析数学学习和现实生活中的平移、旋转、中心对称现象
平移及其基本性质
简单的平移画图
沿坐标轴方向平移后的图形与原图形对应点坐标之间的关系
依次沿两个坐标轴方向平移后所得到的图形与原来图形之间的关系
旋转及其基本性质
简单的旋转画图
图形之间的变换关系分析
中心对称及其基本性质
中心对称画图
中心对称图形
简单的图案欣赏与设计
复习课
练习检测 知识梳理
1.在6×6方格中,将图1中的图形N平移后位置如图2所示,
则下列平移过程中,正确的是( ).
A. 向下移动1格
B.向上移动1格
C.向上移动2格
D.向下移动2格
D
知识点:平移要素(方向与距离)
做一做
2. 将点A(1,-3)向右平移2个单位,再向下平移2个单位后
得到点B(a,b),则 ab= .
练习检测 知识梳理
知识点:
平移坐标有特征,
横坐标左减右加,
纵坐标上加下减.
-15
平移——定义及性质
1. 在平面内,将一个图形沿某个 移动一定的 ,这样
的图形移动称为平移.
2. 平移的性质:
(1)对应线段平行(或共线)且 ,对应点所连的线段 ,
图形上的每个点都沿同一个方向移动了相同的距离;
(2)对应角分别 ,且对应角的两边分别平行、方向一致;
(3)平移变换后的图形与原图形 .
方向
距离
相等
相等
相等
全等
填一填
练习检测 知识梳理
做一做
3. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,
将 △ABC 绕点C 顺时针旋转至△A′B′C,使得点A′ 恰好
落在AB上,则旋转角度为( ).
A.30°
B.60°
C.90°
D.150°
B
知识点:旋转的性质及等边三角形
练习检测 知识梳理
4. 如图,Rt△OAB的直角边 OA 在y轴上,点 B 在第一象限内,
OA=2,AB=1,若将△OAB 绕点 O 按顺时针方向旋转90°,
则点B的对应点的坐标是 .
(2,-1)
知识点:旋转性质,长度与坐标
旋转——定义及性质
1. 定义:在平面内,把一个图形绕着某一个定点沿着某个
方向旋转一定的角度,这样的图形运动称为旋转.这个
定点叫做 ,转动的角叫做 .
2. 图形的旋转有三个基本条件
(1) ;(2) ;(3) .
3. 旋转的性质:
(1)对应点到旋转中心的距离 ;
(2)对应点与旋转中心所连线段的夹角等于 ;
(3)旋转前后的图形 .
旋转中心
旋转角
旋转中心
旋转方向
旋转角
相等
旋转角
全等
填一填
练习检测 知识梳理
5. 正方形ABCD在直角坐标系中的位置如图所示,将正方形
ABCD绕点A顺时针方向旋转180°后,C点的坐标是 .
解析:AB=2,则正方形ABCD绕点A顺时针方向
旋转180°后C的对应点设是,C点的坐标是C′,
则AC′=AC=2,OC′=OA+AC′=3,
故坐标是(3,0).
做一做
(3,0)
中心对称与中心对称图形——区别与联系
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系,中心对
称图形指一个图形本身成中心对称.
联系: 如果将成中心对称的两个图形看成一个整体,则它
们是中心对称图形.如果将中心对称图形对称的部
分看成两个图形,则它们成中心对称.
练习检测 知识梳理
简单的图案设计
(1)确定“基本图案”;
(2)分析轴对称、平移、旋转等变换手法及组合的合理运用.
知识构建
图形的平移与旋转
图形的平移
图形的旋转
中心对称
简单的图案设计
两个图形成中心对称
中心对称图形
拓展提升
6. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC
沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接
A′C,求△A′B′C的周长.
思路:60°的理解、平移的性质
解:由题意可得B′C′=BC,CC′=2,
∴B′C=4,
又∠B=60°,∴△A′B′C为等边三角形,
∴△A′B′C的周长为4×3=12.
拓展提升
7. 如图,在长20m,宽10m的长方形草地内修建了宽2m的
道路,则草地的面积为 m2.
144
思路:将图中道路分别向左、右上平移,
得到右图,此时草地部分的长为
20-2=18m,宽为10-2=8m,
则草地面积为18×8=144m2.
拓展提升
8. 在直角坐标系中的矩形OABC,OA=4,OC=2,将矩形
OABC绕点C逆时针旋转至矩形DEFC,DE经过点B.
求旋转角的大小.
y
x
A
F
D
C
B
o
E
提示:如何理解DE经过点B,特殊角度的
直角三角形及旋转性质
解析:根据OA=4,OC=2,BC=OA,
而由BC=2CD,可以求出∠BCD=60°,
则可得旋转角为30°.
拓展提升
9. 如图,已知△ABC中,∠C=90°, AC=BC= ,将△ABC
绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,
判断BC′与AB′的位置关系并说明理由?
提示:连结BB′,并延长BC′交AB′于点D,
利用三角形全等
解析:如图,连接BB′,
∵△ABC绕点A顺时针方向旋转60°
得到△AB′C′,∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,∴AB=BB′,
再证△ABD′≌△B′BD,即可得BC′⊥AB′.
课堂总结
思考本章的知识框架?
回顾并分析数学学习和现实生活中的平移、旋转、中心对称现象
平移及其基本性质
简单的平移画图
沿坐标轴方向平移后的图形与原图形对应点坐标之间的关系
依次沿两个坐标轴方向平移后所得到的图形与原来图形之间的关系
旋转及其基本性质
简单的旋转画图
图形之间的变换关系分析
中心对称及其基本性质
中心对称画图
中心对称图形
简单的图案欣赏与设计
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
