2020-2021学年北师大版八年级数学下册3.3中心对称 课件(共14张)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册3.3中心对称 课件(共14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
中心对称
回顾
生活中的现象
性质
作图
定义
生活中的
中心对称
中心对称
的性质
中心对称
作图
中心对称
的定义
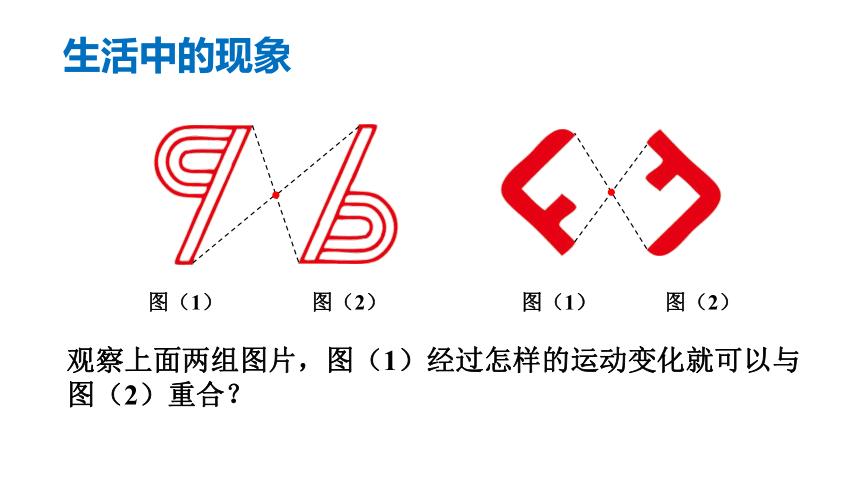
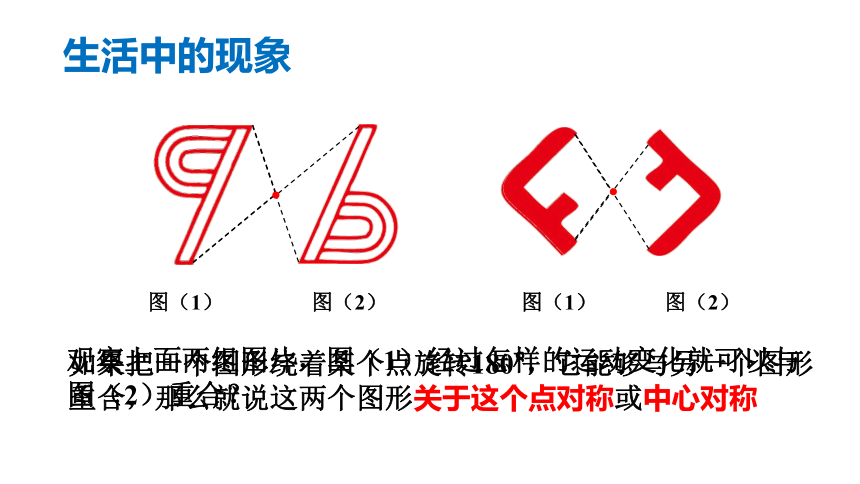
生活中的现象
观察上面两组图片,图(1)经过怎样的运动变化就可以与
图(2)重合?
图(1)
图(2)
图(1)
图(2)
如果把一个图形绕着某个点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
观察上面两组图片,图(1)经过怎样的运动变化就可以与
图(2)重合?
图(1)
图(2)
图(1)
图(2)
生活中的现象
中心对称的定义
如果把一个图形绕着某个点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
对称中心:点O
△ABC与△A'B'C'成中心对称
△ABC与△A'B'C'关于点O对称
,
这个点叫做它们的对称中心.
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
中心对称与旋转
如果把一个图形绕着某个点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.
探索中心对称的性质
自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180°.连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试,并与同伴交流.
A
O
F
E
D
C
B
自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180°.连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试,并与同伴交流.
探索中心对称的性质
①在△ABC与△DEF中,有对应线段相等,对应角相等;
②线段AD、BE、CF都经过点O
成中心对称的两个图形是全等图形;
成中心对称的两个图形中,对应点所连线段经过对称
中心
,且有
OA=OD,
OB=OE,
OC=OF.
M
N
,且被对称中心平分.
中心对称作图
B′
C′
D′
如图,点O是线段AE 的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
解:如图,连接BO并延长至B′,使OB′=OB;
连接CO并延长至C′,使OC′=OC;
连接DO并延长至D′,使OD′=OD;
顺次连接E、B′、C′、D′、A.
图形EB′C′D′A就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
成中心对称的两个图形中,对应点所连
线段经过对称中心,且被对称中心平分.
B′
C′
D′
议一议
请你观察这些图形,它们有什么共同特征?
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形
,这个点叫做
它的对称中心.
中心对称与中心对称图形
中心对称 中心对称图形
定义
区别
联系 如果把一个图形绕着某个点旋转
180°,它能够与另一个图形重合,那么就说这两个图形关于这个点
对称或中心对称.
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做
中心对称图形.
两个图形的关系
一个图形的特征
若把中心对称图形的两部分分别看作两图,则它们成中心对称;
若把中心对称的两图看作一个整体,则为中心对称图形。
B′
C′
D′
轴对称与轴对称图形
中 国
当堂检测
1.下面哪些图片是中心对称图形?
2.下列常见几何图形中,轴对称图形的有______________,
中心对称图形的有____________,既是轴对称图形又是
中心对称图形的有___________.
当堂检测
①线段 ②角 ③等边三角形 ④平行四边形
⑤矩形 ⑥菱形 ⑦圆 ⑧ 等腰梯形
①
①
①
②
③
④
⑤
⑤
⑤
⑥
⑥
⑥
⑦
⑦
⑦
⑧
课堂小结
中心对称和
中心对称图形
中心
对称
中心对
称图形
定义
性质
作图
绕一点旋转180°与另一个图形重合
成中心对称的两个图形中,对应点所连线段
经过对称中心,且被对称中心平分.
绕一点旋转180°与原图重合
B′
C′
D′
中心对称
回顾
生活中的现象
性质
作图
定义
生活中的
中心对称
中心对称
的性质
中心对称
作图
中心对称
的定义
生活中的现象
观察上面两组图片,图(1)经过怎样的运动变化就可以与
图(2)重合?
图(1)
图(2)
图(1)
图(2)
如果把一个图形绕着某个点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
观察上面两组图片,图(1)经过怎样的运动变化就可以与
图(2)重合?
图(1)
图(2)
图(1)
图(2)
生活中的现象
中心对称的定义
如果把一个图形绕着某个点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称
对称中心:点O
△ABC与△A'B'C'成中心对称
△ABC与△A'B'C'关于点O对称
,
这个点叫做它们的对称中心.
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
中心对称与旋转
如果把一个图形绕着某个点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.
探索中心对称的性质
自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180°.连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试,并与同伴交流.
A
O
F
E
D
C
B
自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180°.连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试,并与同伴交流.
探索中心对称的性质
①在△ABC与△DEF中,有对应线段相等,对应角相等;
②线段AD、BE、CF都经过点O
成中心对称的两个图形是全等图形;
成中心对称的两个图形中,对应点所连线段经过对称
中心
,且有
OA=OD,
OB=OE,
OC=OF.
M
N
,且被对称中心平分.
中心对称作图
B′
C′
D′
如图,点O是线段AE 的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
解:如图,连接BO并延长至B′,使OB′=OB;
连接CO并延长至C′,使OC′=OC;
连接DO并延长至D′,使OD′=OD;
顺次连接E、B′、C′、D′、A.
图形EB′C′D′A就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
成中心对称的两个图形中,对应点所连
线段经过对称中心,且被对称中心平分.
B′
C′
D′
议一议
请你观察这些图形,它们有什么共同特征?
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形
,这个点叫做
它的对称中心.
中心对称与中心对称图形
中心对称 中心对称图形
定义
区别
联系 如果把一个图形绕着某个点旋转
180°,它能够与另一个图形重合,那么就说这两个图形关于这个点
对称或中心对称.
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做
中心对称图形.
两个图形的关系
一个图形的特征
若把中心对称图形的两部分分别看作两图,则它们成中心对称;
若把中心对称的两图看作一个整体,则为中心对称图形。
B′
C′
D′
轴对称与轴对称图形
中 国
当堂检测
1.下面哪些图片是中心对称图形?
2.下列常见几何图形中,轴对称图形的有______________,
中心对称图形的有____________,既是轴对称图形又是
中心对称图形的有___________.
当堂检测
①线段 ②角 ③等边三角形 ④平行四边形
⑤矩形 ⑥菱形 ⑦圆 ⑧ 等腰梯形
①
①
①
②
③
④
⑤
⑤
⑤
⑥
⑥
⑥
⑦
⑦
⑦
⑧
课堂小结
中心对称和
中心对称图形
中心
对称
中心对
称图形
定义
性质
作图
绕一点旋转180°与另一个图形重合
成中心对称的两个图形中,对应点所连线段
经过对称中心,且被对称中心平分.
绕一点旋转180°与原图重合
B′
C′
D′
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
