2020-2021学年苏科版七年级下册7.5多边形的内角和与外角和课件(共17张)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册7.5多边形的内角和与外角和课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 734.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览


文档简介
7.5 多边形的内角和与外角和
第7章 平面图形的认识(二)
找出地板中的多边形.
一、复习引入
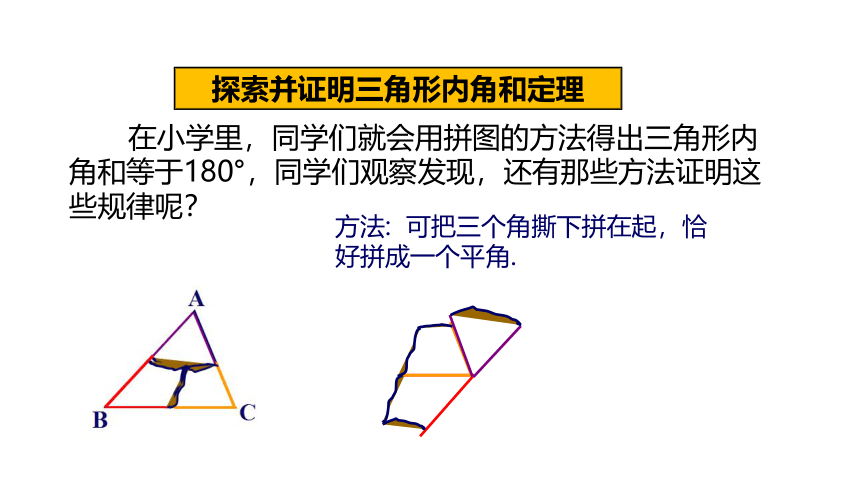
在小学里,同学们就会用拼图的方法得出三角形内角和等于180°,同学们观察发现,还有那些方法证明这些规律呢?
方法: 可把三个角撕下拼在起,恰好拼成一个平角.
探索并证明三角形内角和定理
探索并证明三角形内角和定理
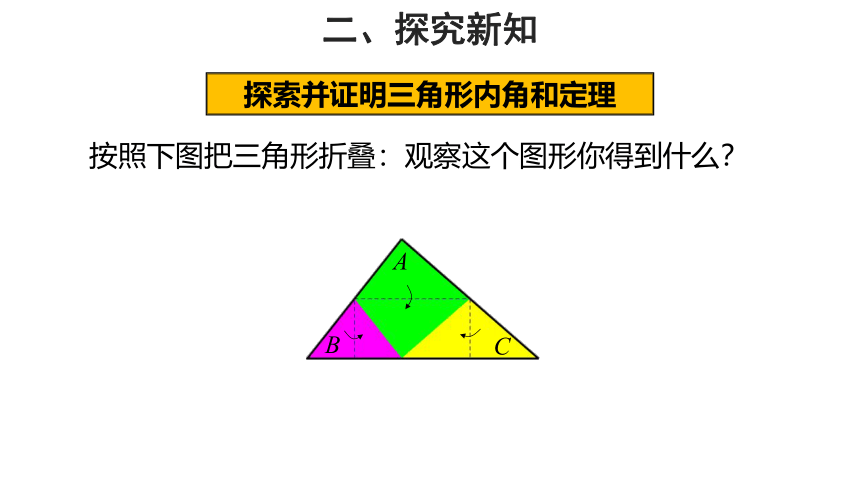
按照下图把三角形折叠:观察这个图形你得到什么?
A
B
C
二、探究新知
探索并证明三角形内角和定理
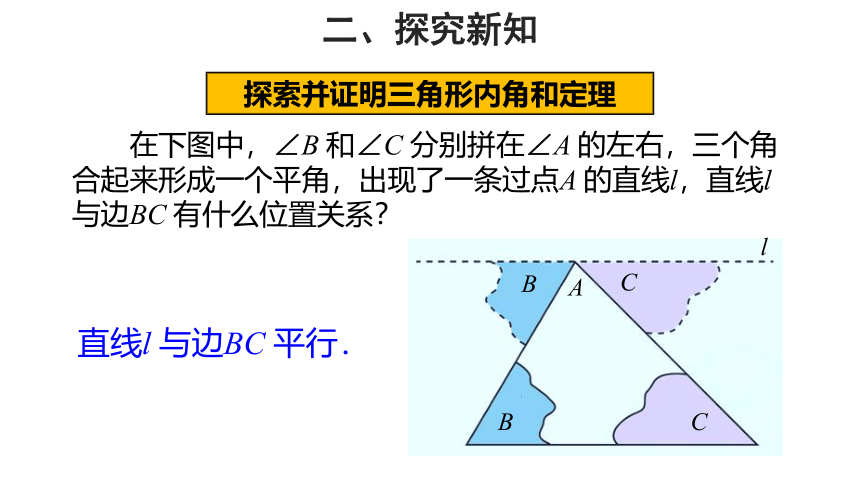
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?
B
B
C
C
A
l
直线l 与边BC 平行.
二、探究新知
探索并证明三角形内角和定理
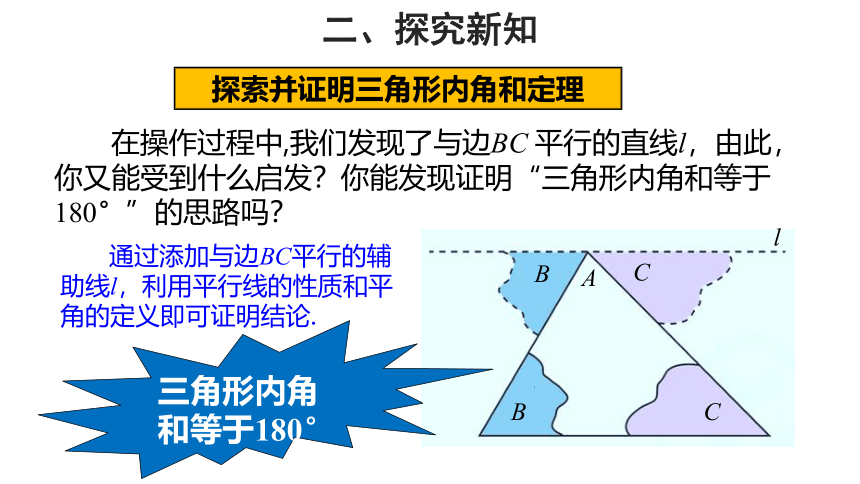
在操作过程中,我们发现了与边BC 平行的直线l,由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
B
B
C
C
A
l
通过添加与边BC平行的辅助线l,利用平行线的性质和平角的定义即可证明结论.
三角形内角和等于180°
二、探究新知
多边形组成的图案
二、探究新知
(1)在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
一个多边形由几条线段组成,就叫做几边形,三角形是最简单的多边形.
(2)多边形中相邻两边组成的角叫做多边形的内角.
如图中的∠A、∠B、∠C、∠D、∠E.
(3)多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
(4)连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
二、探究新知
如图,从五边形ABCDE 的顶点A 出发共有几条对角线?
A
B
C
D
E
二、探究新知
长方形、正方形的内角和等于360°.
任意一个四边形的内角和是否也等于360° 呢?
例如:利用三角形内角和定理证明:
从四边形的一个顶点出发,
可以作1条对角线,它们将四边形分为2个三角形,四边形的内角和等于180°×2=360°.
A
B
C
D
二、探究新知
类比前面的过程,你能探索五边形的内角和吗?
从五边形的一个顶点出发,
可以作2条对角线,它们将四边形分为3个三角形,四边形的内角和等于180°×3=540°.
A
B
C
D
E
六边形、八边形呢
二、探究新知
从四边形、五边形、六边形的内角和的 研究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?
从n 边形的一个顶点出发,可以作(n -3)条对角
线,它们将n 边形分为(n -2)个三角形,这(n -2)
个三角形的内角和就是n 边形的内角和,所以,n 边形
的内角和等于(n -2)×180°.
二、探究新知
我们知道,三角形的内角和是180°,三角形的外角和是360°.得出三角形的外角和是360°有多种方法.如图,你能说说怎样由外角与相邻内角互补的关系得出这个结论吗?
由 ∠1 +∠BAE =180°,∠2 +∠CBF =180°,
∠3 +∠ACD =180°,
得 ∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD =540°
由 ∠1 + ∠2 + ∠3 = 180°,得
∠BAE +∠CBF +∠ACD
= 540° - 180°
= 360°
A
B
C
D
E
F
1
2
3
二、探究新知
如图,仿照上面的方法求四边形的外角和吗?
由 ∠BAD +∠1 =180°,
∠ABC +∠2 =180°,
∠BCD +∠3 =180°,
∠ADC +∠4 =180°,
得∠BAD + ∠1 + ∠ABC
+∠2 +∠BCD +∠3 +∠ADC +∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,得
∠1 +∠2 +∠3 +∠4 =180°×4 - 180°×2 =360°.
A
B
C
1
2
3
D
4
二、探究新知
因为n 边形的每个内角与它相邻的外角是邻补角,
它们的和是180°,所以n 边形内角和加外角和等于:
n · 180°,所以, n 边形的外角和为:
n · 180°-(n -2)· 180°= 360°
任意多边形的外角和等于360°
二、探究新知
1.本节课通过操作活动,探索了三角形内角和与外角和的基本性质.
2.本节课接下来根据三角形内角和与外角和,探索了多边形的内角和与外角和的相关性质.
3.请同学们求解习题中的相关几何问题.
课后小结
再 见
第7章 平面图形的认识(二)
找出地板中的多边形.
一、复习引入
在小学里,同学们就会用拼图的方法得出三角形内角和等于180°,同学们观察发现,还有那些方法证明这些规律呢?
方法: 可把三个角撕下拼在起,恰好拼成一个平角.
探索并证明三角形内角和定理
探索并证明三角形内角和定理
按照下图把三角形折叠:观察这个图形你得到什么?
A
B
C
二、探究新知
探索并证明三角形内角和定理
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?
B
B
C
C
A
l
直线l 与边BC 平行.
二、探究新知
探索并证明三角形内角和定理
在操作过程中,我们发现了与边BC 平行的直线l,由此,你又能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
B
B
C
C
A
l
通过添加与边BC平行的辅助线l,利用平行线的性质和平角的定义即可证明结论.
三角形内角和等于180°
二、探究新知
多边形组成的图案
二、探究新知
(1)在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
一个多边形由几条线段组成,就叫做几边形,三角形是最简单的多边形.
(2)多边形中相邻两边组成的角叫做多边形的内角.
如图中的∠A、∠B、∠C、∠D、∠E.
(3)多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
(4)连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
二、探究新知
如图,从五边形ABCDE 的顶点A 出发共有几条对角线?
A
B
C
D
E
二、探究新知
长方形、正方形的内角和等于360°.
任意一个四边形的内角和是否也等于360° 呢?
例如:利用三角形内角和定理证明:
从四边形的一个顶点出发,
可以作1条对角线,它们将四边形分为2个三角形,四边形的内角和等于180°×2=360°.
A
B
C
D
二、探究新知
类比前面的过程,你能探索五边形的内角和吗?
从五边形的一个顶点出发,
可以作2条对角线,它们将四边形分为3个三角形,四边形的内角和等于180°×3=540°.
A
B
C
D
E
六边形、八边形呢
二、探究新知
从四边形、五边形、六边形的内角和的 研究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?
从n 边形的一个顶点出发,可以作(n -3)条对角
线,它们将n 边形分为(n -2)个三角形,这(n -2)
个三角形的内角和就是n 边形的内角和,所以,n 边形
的内角和等于(n -2)×180°.
二、探究新知
我们知道,三角形的内角和是180°,三角形的外角和是360°.得出三角形的外角和是360°有多种方法.如图,你能说说怎样由外角与相邻内角互补的关系得出这个结论吗?
由 ∠1 +∠BAE =180°,∠2 +∠CBF =180°,
∠3 +∠ACD =180°,
得 ∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD =540°
由 ∠1 + ∠2 + ∠3 = 180°,得
∠BAE +∠CBF +∠ACD
= 540° - 180°
= 360°
A
B
C
D
E
F
1
2
3
二、探究新知
如图,仿照上面的方法求四边形的外角和吗?
由 ∠BAD +∠1 =180°,
∠ABC +∠2 =180°,
∠BCD +∠3 =180°,
∠ADC +∠4 =180°,
得∠BAD + ∠1 + ∠ABC
+∠2 +∠BCD +∠3 +∠ADC +∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,得
∠1 +∠2 +∠3 +∠4 =180°×4 - 180°×2 =360°.
A
B
C
1
2
3
D
4
二、探究新知
因为n 边形的每个内角与它相邻的外角是邻补角,
它们的和是180°,所以n 边形内角和加外角和等于:
n · 180°,所以, n 边形的外角和为:
n · 180°-(n -2)· 180°= 360°
任意多边形的外角和等于360°
二、探究新知
1.本节课通过操作活动,探索了三角形内角和与外角和的基本性质.
2.本节课接下来根据三角形内角和与外角和,探索了多边形的内角和与外角和的相关性质.
3.请同学们求解习题中的相关几何问题.
课后小结
再 见
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
