华东师大版七年级下册数学课件:6.2.2 解一元一次方程3(共22张)
文档属性
| 名称 | 华东师大版七年级下册数学课件:6.2.2 解一元一次方程3(共22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 19:46:13 | ||
图片预览







文档简介
第6章 一元一次方程
6.2 解一元一次方程
2. 解一元一次方程
教学目标
教学重点与难点
重点:会列一元一次方程解简单的应用题.
难点:正确列出符合题意的一元一次方程.
1.进一步掌握解一元一次方程。?
2. 会列一元一次方程解简单的应用题.
3.培养学生数学建模的能力.
一.去分母:
当方程中的系数出现分数,将方程的两边都乘以
同一个数(各分母的最小公倍数),去掉方程中的
分母的变形称为“去分母”.
注意:不要漏乘不含分母的项.
二.解一元一次方程的一般步骤是:
说明:解一元一次方程的一般步骤,并不是每题
都要全部用到,要根据具体题目取舍.
温故夯基
(1) 去分母;
(2) 去括号;
(3) 移项;
(4) 合并同类项;
(5) 系数化为1.
巩固练习
B
A
1.在解方程 时,方程两边同时乘以6,
去分母后,正确的是( ).
A.2x-1+6x=3(3x+1)
B.2(x-1)+6x=3(3x+1)
C.2(x-1)+x=3(3x+1)
D.(x-1)+x=3(x+1)
2.若关于x的一元一次方程 的解
是x=-1,则k的值是( ).
A. 1 B. C. D.0
D
3.下列变形正确的是( ).
A.由 ,得2(x-2)-5x+2=4
B.由 ,得4(2x-1)-3(3x-1)=1
C.由 ,得4(x-1)-(9x+2)=8
D.由 ,得3(x-1)+6x=2(2x-3)+12
去分母得:2(x+5)+3(x-1)=12,
去括号得:2x+10+3x-3=12,
移项得:2x+3x=12-10+3,
合并同类项得:5x=5,
系数化为1得:x=1.
1
解方程2x-3=3得x=3.
把x=3代入方程 得:
解方程 得:
m=2.
2
4.若代数式 与 的和为2,则x的值为____.
5.已知方程2x-3=3和方程 有相同的解,则m的值为____.
学习新知
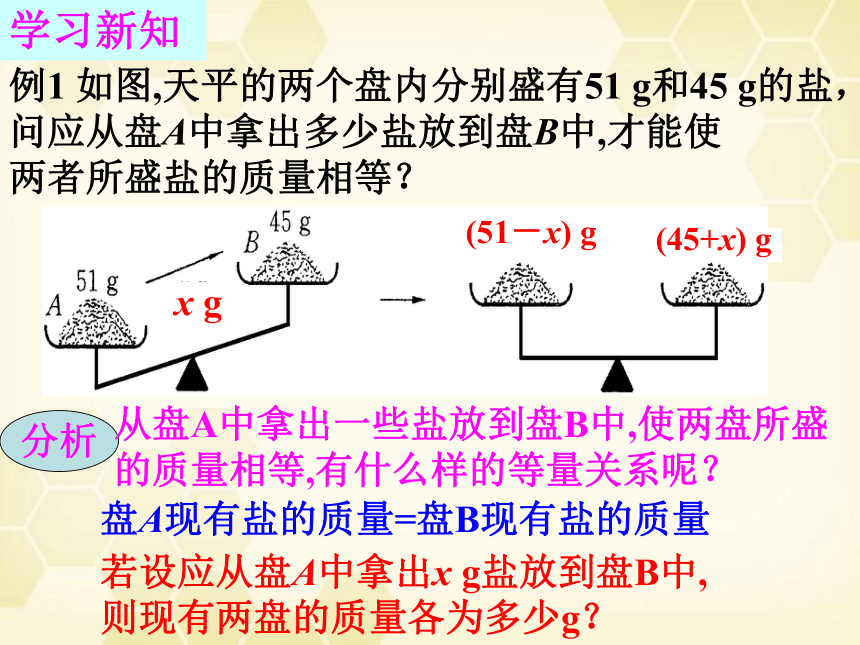
例1 如图,天平的两个盘内分别盛有51 g和45 g的盐,问应从盘A中拿出多少盐放到盘B中,才能使
两者所盛盐的质量相等?
分析
从盘A中拿出一些盐放到盘B中,使两盘所盛
的质量相等,有什么样的等量关系呢?
盘A现有盐的质量=盘B现有盐的质量
若设应从盘A中拿出x g盐放到盘B中,
则现有两盘的质量各为多少g?
x g
(51-x) g
(45+x) g
学习新知
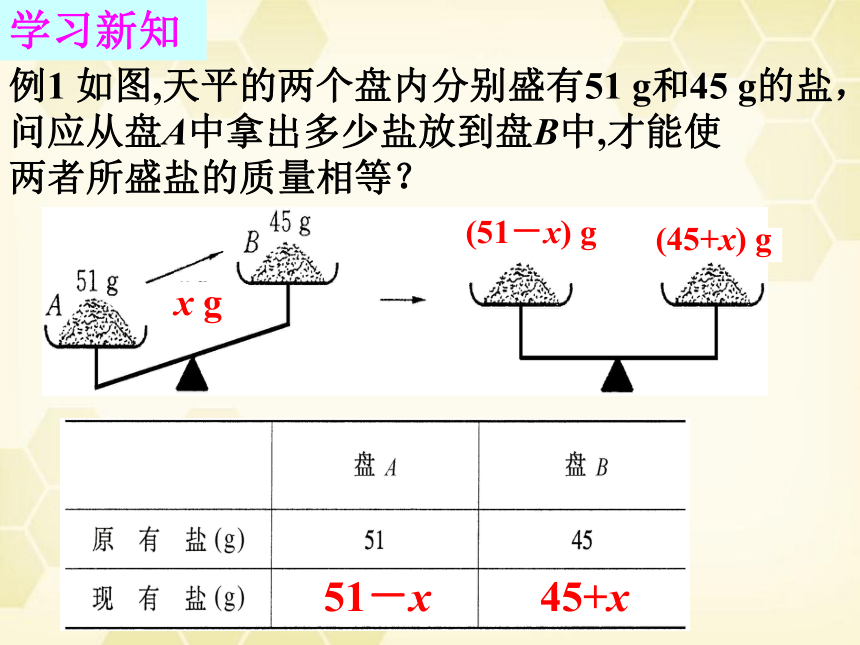
例1 如图,天平的两个盘内分别盛有51 g和45 g的盐,问应从盘A中拿出多少盐放到盘B中,才能使
两者所盛盐的质量相等?
x g
(51-x) g
(45+x) g
51-x
45+x
学习新知
例1 如图,天平的两个盘内分别盛有51 g和45 g的盐,问应从盘A中拿出多少盐放到盘B中,才能使
两者所盛盐的质量相等?
解: 设应从盘A中拿出x g盐放到盘B中,
依题意得:
51-x=45+x.
解这个方程,得:
x=3.
经检验,符合题意.
答:应从盘A中拿出3 g盐放到盘B中.
方法总结
1.列一元一次方程解答实际问题的关键是弄清题意,找出等量关系,列出方程.求得方程的解后,经过检验,就可得到实际问题的解答.
2.列一元一次方程解应用题的一般步骤:
(1)设未知数;(要注意单位)
(2)根据等量关系,列出方程;
(3)解方程;
(4)检验方程的解是否符合题意;
(5)作答.(要注意单位)
随堂练习
1.学校大扫除,某班原分成两个小组,第一小组24人
打扫教室,第二小组21人打扫包干区.这次根据
工作需要,要使第二组人数是第一组人数的2倍,
那么应从第一组调多少人到第二组?
解:设应从第一组调x人到第二组,
依题意得:
21+x=2(24-x).
解这个方程,得:
x=9.
经检验,符合题意.
答:应从第一组调9人到第二组.
解:设从甲煤场运煤x吨到乙煤场,
依题意得:518-x=3(106+x),
解这个方程,得:x=50.
经检验,符合题意.
答:从甲煤场运煤50吨到乙煤场.
2.已知甲煤场有煤518吨,乙煤场有煤106 吨,为了使
甲煤场存煤是乙煤场的3倍,需要从甲煤场运煤多少
吨到乙煤场?
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
读题,找找看,题目告诉了我们哪些等量关系?
1.男同学搬砖数+女同学搬砖数=搬砖总数;
2.男同学人数+女同学人数=65;
3.男同学搬砖数= 女同学搬砖数.
女同学搬砖数= 男同学搬砖数.
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
分析
若设新团员中有x名男同学,则女同学有 名.
(65-x)
请同学们一起完成下表
65-x
8×4
32x
24(65-x)
32x+24(65-x)=1800
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
解: 设新团员中有x名男同学,
依题意得:
32x+24(65-x)=1800.
解这个方程,得:
x=30.
经检验,符合题意.
答: 这些新团员中有30名男同学.
若设男同学搬砖x块,
则方程怎么列呢?
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
解: 设男同学搬砖x块,
依题意得:
解这个方程,得:
x=960.
经检验,符合题意.
答: 这些新团员中有30名男同学.
分析:
400米
大部分路程
1分零5秒
随堂练习
1.学校田径队的小刚在400米跑测试时,先以6米/秒
的速度跑完了大部分路程,最后以8米/秒的速度冲刺
到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了
多少时间?
设小刚在冲刺阶段花了t秒?
=65秒
t秒
(65-t)秒
随堂练习
1.学校田径队的小刚在400米跑测试时,先以6米/秒
的速度跑完了大部分路程,最后以8米/秒的速度冲刺
到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了
多少时间?
解:设小刚在冲刺阶段花了t秒,
6(65-t)+8t=400.
依题意得:
解这个方程,得:
t=5.
经检验,符合题意.
答:设小刚在冲刺阶段花了5秒.
2.A、B两地之间的路程为180km,甲骑自行车从
A地出发,乙开汽车从B地出发,速度是甲的5倍,
两人同时出发,相向而行,经过2小时相遇,
则乙开车的速度是多少?
解:设甲骑车的速度是x千米/时,
则乙开车的速度是5x千米/时,
依题意得:
2(x+5x)=180.
解这个方程,得:
x=15.
则5x=75.
经检验,符合题意.
答:乙开车的速度是75千米/时.
1.列一元一次方程解答实际问题的关键是弄清题意,找出等量关系,列出方程.求得方程的解后,经过检验,就可得到实际问题的解答.
2.列一元一次方程解应用题的一般步骤:
(1)设未知数;(要注意单位)
(2)根据等量关系,列出方程;
(3)解方程;
(4)检验方程的解是否符合题意;
(5)作答.(要注意单位)
课堂小结
作业与课外学习任务
1.练习作业:学习检测P9-15 第1至20题
书面课本P14 习题6.2.2 4,5
2.课外学习任务:
预习课本P16 6.3 实践与探索
教学反馈:
作业存在的主要问题:
6.2 解一元一次方程
2. 解一元一次方程
教学目标
教学重点与难点
重点:会列一元一次方程解简单的应用题.
难点:正确列出符合题意的一元一次方程.
1.进一步掌握解一元一次方程。?
2. 会列一元一次方程解简单的应用题.
3.培养学生数学建模的能力.
一.去分母:
当方程中的系数出现分数,将方程的两边都乘以
同一个数(各分母的最小公倍数),去掉方程中的
分母的变形称为“去分母”.
注意:不要漏乘不含分母的项.
二.解一元一次方程的一般步骤是:
说明:解一元一次方程的一般步骤,并不是每题
都要全部用到,要根据具体题目取舍.
温故夯基
(1) 去分母;
(2) 去括号;
(3) 移项;
(4) 合并同类项;
(5) 系数化为1.
巩固练习
B
A
1.在解方程 时,方程两边同时乘以6,
去分母后,正确的是( ).
A.2x-1+6x=3(3x+1)
B.2(x-1)+6x=3(3x+1)
C.2(x-1)+x=3(3x+1)
D.(x-1)+x=3(x+1)
2.若关于x的一元一次方程 的解
是x=-1,则k的值是( ).
A. 1 B. C. D.0
D
3.下列变形正确的是( ).
A.由 ,得2(x-2)-5x+2=4
B.由 ,得4(2x-1)-3(3x-1)=1
C.由 ,得4(x-1)-(9x+2)=8
D.由 ,得3(x-1)+6x=2(2x-3)+12
去分母得:2(x+5)+3(x-1)=12,
去括号得:2x+10+3x-3=12,
移项得:2x+3x=12-10+3,
合并同类项得:5x=5,
系数化为1得:x=1.
1
解方程2x-3=3得x=3.
把x=3代入方程 得:
解方程 得:
m=2.
2
4.若代数式 与 的和为2,则x的值为____.
5.已知方程2x-3=3和方程 有相同的解,则m的值为____.
学习新知
例1 如图,天平的两个盘内分别盛有51 g和45 g的盐,问应从盘A中拿出多少盐放到盘B中,才能使
两者所盛盐的质量相等?
分析
从盘A中拿出一些盐放到盘B中,使两盘所盛
的质量相等,有什么样的等量关系呢?
盘A现有盐的质量=盘B现有盐的质量
若设应从盘A中拿出x g盐放到盘B中,
则现有两盘的质量各为多少g?
x g
(51-x) g
(45+x) g
学习新知
例1 如图,天平的两个盘内分别盛有51 g和45 g的盐,问应从盘A中拿出多少盐放到盘B中,才能使
两者所盛盐的质量相等?
x g
(51-x) g
(45+x) g
51-x
45+x
学习新知
例1 如图,天平的两个盘内分别盛有51 g和45 g的盐,问应从盘A中拿出多少盐放到盘B中,才能使
两者所盛盐的质量相等?
解: 设应从盘A中拿出x g盐放到盘B中,
依题意得:
51-x=45+x.
解这个方程,得:
x=3.
经检验,符合题意.
答:应从盘A中拿出3 g盐放到盘B中.
方法总结
1.列一元一次方程解答实际问题的关键是弄清题意,找出等量关系,列出方程.求得方程的解后,经过检验,就可得到实际问题的解答.
2.列一元一次方程解应用题的一般步骤:
(1)设未知数;(要注意单位)
(2)根据等量关系,列出方程;
(3)解方程;
(4)检验方程的解是否符合题意;
(5)作答.(要注意单位)
随堂练习
1.学校大扫除,某班原分成两个小组,第一小组24人
打扫教室,第二小组21人打扫包干区.这次根据
工作需要,要使第二组人数是第一组人数的2倍,
那么应从第一组调多少人到第二组?
解:设应从第一组调x人到第二组,
依题意得:
21+x=2(24-x).
解这个方程,得:
x=9.
经检验,符合题意.
答:应从第一组调9人到第二组.
解:设从甲煤场运煤x吨到乙煤场,
依题意得:518-x=3(106+x),
解这个方程,得:x=50.
经检验,符合题意.
答:从甲煤场运煤50吨到乙煤场.
2.已知甲煤场有煤518吨,乙煤场有煤106 吨,为了使
甲煤场存煤是乙煤场的3倍,需要从甲煤场运煤多少
吨到乙煤场?
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
读题,找找看,题目告诉了我们哪些等量关系?
1.男同学搬砖数+女同学搬砖数=搬砖总数;
2.男同学人数+女同学人数=65;
3.男同学搬砖数= 女同学搬砖数.
女同学搬砖数= 男同学搬砖数.
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
分析
若设新团员中有x名男同学,则女同学有 名.
(65-x)
请同学们一起完成下表
65-x
8×4
32x
24(65-x)
32x+24(65-x)=1800
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
解: 设新团员中有x名男同学,
依题意得:
32x+24(65-x)=1800.
解这个方程,得:
x=30.
经检验,符合题意.
答: 这些新团员中有30名男同学.
若设男同学搬砖x块,
则方程怎么列呢?
例2 学校团委组织65名新团员为学校建花坛搬砖.
女同学每人每次搬6块,男同学每人每次搬8块,
每人各搬了4次,共搬了1800块.问这些新团员中
有多少名男同学?
例题精析
解: 设男同学搬砖x块,
依题意得:
解这个方程,得:
x=960.
经检验,符合题意.
答: 这些新团员中有30名男同学.
分析:
400米
大部分路程
1分零5秒
随堂练习
1.学校田径队的小刚在400米跑测试时,先以6米/秒
的速度跑完了大部分路程,最后以8米/秒的速度冲刺
到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了
多少时间?
设小刚在冲刺阶段花了t秒?
=65秒
t秒
(65-t)秒
随堂练习
1.学校田径队的小刚在400米跑测试时,先以6米/秒
的速度跑完了大部分路程,最后以8米/秒的速度冲刺
到达终点,成绩为1分零5秒,问小刚在冲刺阶段花了
多少时间?
解:设小刚在冲刺阶段花了t秒,
6(65-t)+8t=400.
依题意得:
解这个方程,得:
t=5.
经检验,符合题意.
答:设小刚在冲刺阶段花了5秒.
2.A、B两地之间的路程为180km,甲骑自行车从
A地出发,乙开汽车从B地出发,速度是甲的5倍,
两人同时出发,相向而行,经过2小时相遇,
则乙开车的速度是多少?
解:设甲骑车的速度是x千米/时,
则乙开车的速度是5x千米/时,
依题意得:
2(x+5x)=180.
解这个方程,得:
x=15.
则5x=75.
经检验,符合题意.
答:乙开车的速度是75千米/时.
1.列一元一次方程解答实际问题的关键是弄清题意,找出等量关系,列出方程.求得方程的解后,经过检验,就可得到实际问题的解答.
2.列一元一次方程解应用题的一般步骤:
(1)设未知数;(要注意单位)
(2)根据等量关系,列出方程;
(3)解方程;
(4)检验方程的解是否符合题意;
(5)作答.(要注意单位)
课堂小结
作业与课外学习任务
1.练习作业:学习检测P9-15 第1至20题
书面课本P14 习题6.2.2 4,5
2.课外学习任务:
预习课本P16 6.3 实践与探索
教学反馈:
作业存在的主要问题:
