华东师大版七年级下册数学课件:6.2.2 解一元一次方程1(共25张)
文档属性
| 名称 | 华东师大版七年级下册数学课件:6.2.2 解一元一次方程1(共25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 825.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 19:55:38 | ||
图片预览







文档简介
第6章 一元一次方程
6.2 解一元一次方程
2. 解一元一次方程
教学目标
教学重点与难点
重点:一元一次方程的概念和解一元一次方程.
难点:对一元一次方程的理解和正确解一元一次
方程.
1.在理解和掌握一元一次方程的概念。?
2. 会利用去括号和合并同类项的知识解一元一次
方程.
3.进一步提高学生解一元一次方程的技能.
温故夯基
1.方程的定义:
含有未知数的等式.
2.方程的解:
使方程左右两边相等的未知数的值.
3.检验一个数是否是方程的解方法:
将这个数分别代入原方程的左边和右边计算代数式的值,
如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
4.移项:
将方程中的某些项改变符号后,从方程的
一边移到另一边的变形叫做移项 。
5.系数化为1:
将方程的两边都除以未知数的系数(或乘以未知数
的系数的倒数)的变形 .
巩固练习
1.方程2x-3=5的解是( ).
A. 3 B. 4 C. 5 D. 6
B
2.解方程-3x+5=2x-1,移项正确的是( ).
A. 3x-2x=-1+5 B. -3x-2x=5-1
C. 3x-2x=-1-5 D. -3x-2x=-1-5
D
3.下列计算或变形正确的是( ).
A. 3x+2y=5xy B. 若 4x=-4,则x=1
C. 若x=y,则ax=ay D. 3x2-4x2=-1
C
4.方程3x+5=8的解是 .
x=1
5.方程 的解是 .
6.对有理数a,b,现规定运算★的意义是:
a★b=a+2b,则方程3x★4=2的解是 .
∵ a★b=a+2b,
∴ 3x★4=3x+2×4=3x+8,
∵ 3x★4=2,
∴ 3x+8=2,
∴ 3x=-6,
∴ x=-2.
学习新知
前面我们遇到的一些方程,例如:
(1)2x-3=5;
(2)-3x+5=2x-1;
它们都有一个共同特点:
它们都有什么共同特点呢?
它们都只含有一个未知数,并且含有未知数的式子
都是整式,未知数的次数都是1.
一元一次方程
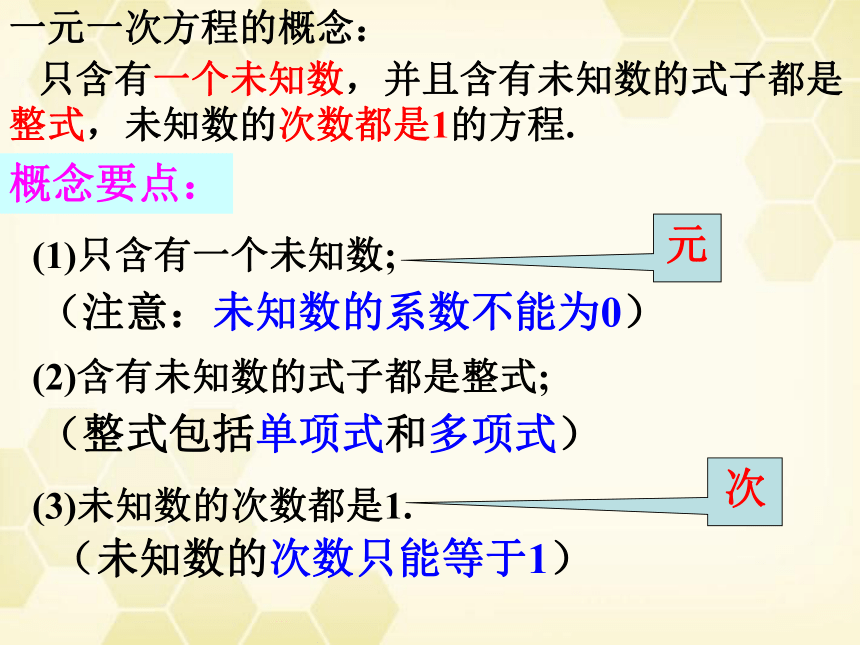
一元一次方程的概念:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数都是1的方程.
概念要点:
(1)只含有一个未知数;
(2)含有未知数的式子都是整式;
(3)未知数的次数都是1.
元
(注意:未知数的系数不能为0)
(整式包括单项式和多项式)
次
(未知数的次数只能等于1)
随堂练习
下列各式中,是方程的有 ,
是一元一次方程的是 .
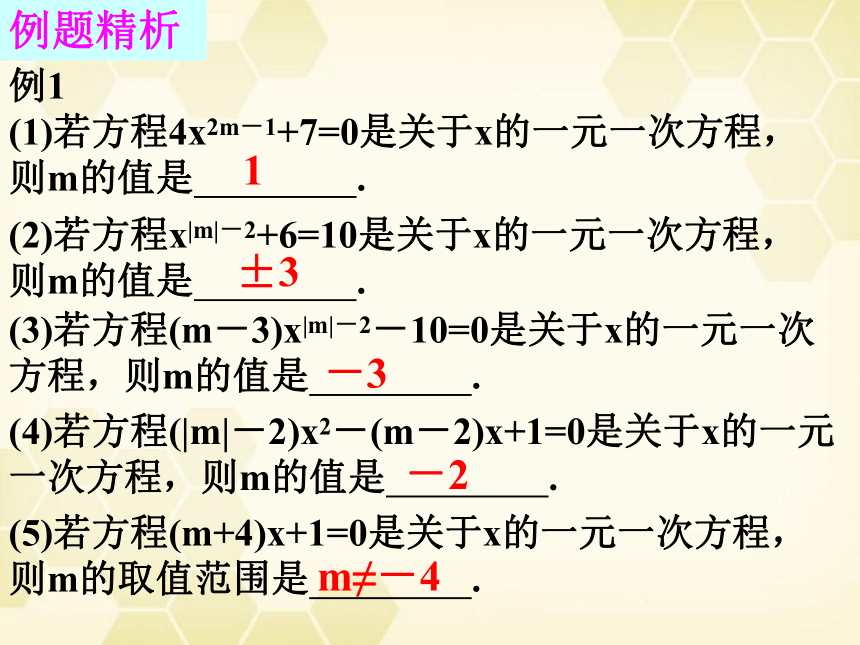
例1
(1)若方程4x2m-1+7=0是关于x的一元一次方程,
则m的值是 .
例题精析
1
(2)若方程x|m|-2+6=10是关于x的一元一次方程,
则m的值是 .
±3
(3)若方程(m-3)x|m|-2-10=0是关于x的一元一次方程,则m的值是 .
-3
(4)若方程(|m|-2)x2-(m-2)x+1=0是关于x的一元一次方程,则m的值是 .
(5)若方程(m+4)x+1=0是关于x的一元一次方程,
则m的取值范围是 .
-2
m≠-4
例题精析
例2 若(m-4)x2|m|-7-4m=0是关于x的一元一次
方程,求m2-2m+1995的值.
解:依题意得:
2|m|-7=1
且m-4≠0.
由2|m|-7=1得|m|=4,
∴m=±4.
由m-4≠0得m≠4,
∴m=-4.
当m=-4时,
m2-2m+1995=(-4)2-2×(-4)+1995
=16+8+1995
=2019.
随堂练习
1.方程(m-2)x|m|-1+8=0是关于x的一元一次方程,求m的值及方程的解.
解:依题意得:
|m|-1=1
且m-2≠0.
由|m|-1=1得|m|=2,
∴m=±2.
由m-2≠0得m≠2,
∴ m=-2.
∴ 一元一次方程是-4x+8=0,
解得: x=2.
2. 已知方程(m+5)x|m|-4+18=0是关于x的一元一次
方程,求:
(1)m的值; (2)3(4m-1)-2(3m+2)的值.
解:(1)依题意得:
|m|-4=1
且m+5≠0.
由|m|-4=1得|m|=5,
∴m=±5.
由m+5≠0得m≠-5,
∴ m=5.
(2)当m=5时,
原式=12m-3-6m-4
=6m-7
=6×5-7
=23.
温故夯基
1.去括号法则:
(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号;
(2)括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
加不变,减全变.
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
系数相加作系数,
字母及其指数不变.
例题精析
例3 解下列方程:
(1) 3(x-2)+1=x-(2x-1);
(2) 2(x-5)-(3x+1)=4(1-x);
(3) 5(x+8)-5=6(2x-7).
解:(1)
去括号得:
3x-6+1=x-2x+1,
即 3x-5=-x+1.
移项,得:
3x+x=1+5,
即 4x=6.
两边都除以4,得:
去括号
合并同类项
移项
系数化为1
例题精析
例3 解下列方程:
(2) 2(x-5)-(3x+1)=4(1-x);
(3) 5(x+8)-5=6(2x-7).
(2)
去括号得:
2x-10-3x-1=4-4x,
即 -x-11=4-4x.
移项,得:
-x+4x=4+11,
即 3x=15.
两边都除以3,得:
x=5.
(3)去括号得:
5x+40-5=12x-42,
即 5x+35=12x-42.
移项,得:
5x-12x=-42-35,
即 -7x=-77.
两边都除以-7,得:
x=11.
随堂练习
解下列方程:
(1) 5(x+2)=2(5x-1);
(2) (x+1)-2(x-1)=1-3x;
(3) 2(x-2)-(4x-1)=3(1-x).
去括号得:5x+10=10x-2,
移项,得:5x-10x=-2-10,即-5x=-12.
两边都除以-5,得:
去括号得:x+1-2x+2=1-3x,即-x+3=1-3x.
移项,得:-x+3x=1-3,即2x=-2.
两边都除以2,得:x=-1.
去括号得:2x-4-4x+1=3-3x,即-2x-3=3-3x.
移项,得:-2x+3x=3+3,即x=6.
例4 当x取何值时,代数式2x+3的值与3(1-x)的值
互为相反数?
例题精析
解:依题意得:
(2x+3)+3(1-x)=0,
去括号得:
2x+3+3-3x=0,
即 -x+6=0.
移项,得:
x=6.
∴ 当x=6时,代数式2x+3的值与3(1-x)的值互为
相反数.
例5 当x取何值时,代数式5(2-x)的值比代数式
9(2x-1)的值小4?
解:依题意得:
5(2-x)-9(2x-1)=-4,
去括号得:
10-5x-18x+9=-4,
即 -23x+19=-4.
移项得: -23x=-4-19,
即 -23x=-23.
两边都除以-23,得:
x=1.
∴当x=1时,代数式5(2-x)的值比代数式9(2x-1)的值小4.
随堂练习
1.当x取何值时,代数式3(2-x)的值与2(3+x)的值
相等?
解:依题意得:
3(2-x)=2(3+x),
去括号得:
6-3x=6+2x,
移项得: -3x-2x=6-6,
即 -5x=0.
两边都除以-5,得:
x=0.
∴当x=0时,代数式3(2-x)的值与2(3+x)的值相等.
2. 当y取何值时,代数式2(3y+4)的值比代数式
5(2y-7)的值大3?
随堂练习
解:依题意得:
2(3y+4)-5(2y-7)=3,
去括号得:
6y+8-10y+35=3,
即 -4y+43=3.
移项得: -4y=3-43,
即 -4y=-40.
两边都除以-4,得:
y=10.
∴当y=10时,代数式2(3y+4)的值比代数式5(2y-7)的值大3.
一、一元一次方程的概念:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数都是1的方程.
概念要点:
(1)只含有一个未知数;
(2)含有未知数的式子都是整式;
(3)未知数的次数都是1.
(注意:未知数的系数不能为0)
(整式包括多项式和多项式)
(未知数的次数只能等于1)
课堂小结
二、解含有括号的一元一次方程的步骤:
1.去括号;
2.合并同类项;
3.移项;
4.系数化为1.
作 业
1.当x取何值时,代数式12-3(6-x)的值与5(4-x)的
值互为相反数?
2.当y取何值时,代数式2(3y-1)的值比3(y+1)的值
大4?
解:依题意得: 12-3(6-x)+5(4-x)=0,
去括号得: 12-18+3x+20-5x=0,即-2x+14=0.
移项得:-2x=-14.
两边都除以-2,得:x=7.
解:依题意得: 2(3y-1)-3(y+1)=4,
去括号得: 6y-2-3y-3=4,即3y-5=4.
移项得:3y=9.
两边都除以3,得:y=3.
作业与课外学习任务
1.练习作业:学习检测P7-9 第1至20题
书面课本P14 习题6.2.2 1
2.课外学习任务:
预习课本P10 6.2.2 解一元一次方程 例5
(含分母的一元一次方程的解法)
教学反馈:
作业存在的主要问题:
6.2 解一元一次方程
2. 解一元一次方程
教学目标
教学重点与难点
重点:一元一次方程的概念和解一元一次方程.
难点:对一元一次方程的理解和正确解一元一次
方程.
1.在理解和掌握一元一次方程的概念。?
2. 会利用去括号和合并同类项的知识解一元一次
方程.
3.进一步提高学生解一元一次方程的技能.
温故夯基
1.方程的定义:
含有未知数的等式.
2.方程的解:
使方程左右两边相等的未知数的值.
3.检验一个数是否是方程的解方法:
将这个数分别代入原方程的左边和右边计算代数式的值,
如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
4.移项:
将方程中的某些项改变符号后,从方程的
一边移到另一边的变形叫做移项 。
5.系数化为1:
将方程的两边都除以未知数的系数(或乘以未知数
的系数的倒数)的变形 .
巩固练习
1.方程2x-3=5的解是( ).
A. 3 B. 4 C. 5 D. 6
B
2.解方程-3x+5=2x-1,移项正确的是( ).
A. 3x-2x=-1+5 B. -3x-2x=5-1
C. 3x-2x=-1-5 D. -3x-2x=-1-5
D
3.下列计算或变形正确的是( ).
A. 3x+2y=5xy B. 若 4x=-4,则x=1
C. 若x=y,则ax=ay D. 3x2-4x2=-1
C
4.方程3x+5=8的解是 .
x=1
5.方程 的解是 .
6.对有理数a,b,现规定运算★的意义是:
a★b=a+2b,则方程3x★4=2的解是 .
∵ a★b=a+2b,
∴ 3x★4=3x+2×4=3x+8,
∵ 3x★4=2,
∴ 3x+8=2,
∴ 3x=-6,
∴ x=-2.
学习新知
前面我们遇到的一些方程,例如:
(1)2x-3=5;
(2)-3x+5=2x-1;
它们都有一个共同特点:
它们都有什么共同特点呢?
它们都只含有一个未知数,并且含有未知数的式子
都是整式,未知数的次数都是1.
一元一次方程
一元一次方程的概念:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数都是1的方程.
概念要点:
(1)只含有一个未知数;
(2)含有未知数的式子都是整式;
(3)未知数的次数都是1.
元
(注意:未知数的系数不能为0)
(整式包括单项式和多项式)
次
(未知数的次数只能等于1)
随堂练习
下列各式中,是方程的有 ,
是一元一次方程的是 .
例1
(1)若方程4x2m-1+7=0是关于x的一元一次方程,
则m的值是 .
例题精析
1
(2)若方程x|m|-2+6=10是关于x的一元一次方程,
则m的值是 .
±3
(3)若方程(m-3)x|m|-2-10=0是关于x的一元一次方程,则m的值是 .
-3
(4)若方程(|m|-2)x2-(m-2)x+1=0是关于x的一元一次方程,则m的值是 .
(5)若方程(m+4)x+1=0是关于x的一元一次方程,
则m的取值范围是 .
-2
m≠-4
例题精析
例2 若(m-4)x2|m|-7-4m=0是关于x的一元一次
方程,求m2-2m+1995的值.
解:依题意得:
2|m|-7=1
且m-4≠0.
由2|m|-7=1得|m|=4,
∴m=±4.
由m-4≠0得m≠4,
∴m=-4.
当m=-4时,
m2-2m+1995=(-4)2-2×(-4)+1995
=16+8+1995
=2019.
随堂练习
1.方程(m-2)x|m|-1+8=0是关于x的一元一次方程,求m的值及方程的解.
解:依题意得:
|m|-1=1
且m-2≠0.
由|m|-1=1得|m|=2,
∴m=±2.
由m-2≠0得m≠2,
∴ m=-2.
∴ 一元一次方程是-4x+8=0,
解得: x=2.
2. 已知方程(m+5)x|m|-4+18=0是关于x的一元一次
方程,求:
(1)m的值; (2)3(4m-1)-2(3m+2)的值.
解:(1)依题意得:
|m|-4=1
且m+5≠0.
由|m|-4=1得|m|=5,
∴m=±5.
由m+5≠0得m≠-5,
∴ m=5.
(2)当m=5时,
原式=12m-3-6m-4
=6m-7
=6×5-7
=23.
温故夯基
1.去括号法则:
(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号;
(2)括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
加不变,减全变.
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
系数相加作系数,
字母及其指数不变.
例题精析
例3 解下列方程:
(1) 3(x-2)+1=x-(2x-1);
(2) 2(x-5)-(3x+1)=4(1-x);
(3) 5(x+8)-5=6(2x-7).
解:(1)
去括号得:
3x-6+1=x-2x+1,
即 3x-5=-x+1.
移项,得:
3x+x=1+5,
即 4x=6.
两边都除以4,得:
去括号
合并同类项
移项
系数化为1
例题精析
例3 解下列方程:
(2) 2(x-5)-(3x+1)=4(1-x);
(3) 5(x+8)-5=6(2x-7).
(2)
去括号得:
2x-10-3x-1=4-4x,
即 -x-11=4-4x.
移项,得:
-x+4x=4+11,
即 3x=15.
两边都除以3,得:
x=5.
(3)去括号得:
5x+40-5=12x-42,
即 5x+35=12x-42.
移项,得:
5x-12x=-42-35,
即 -7x=-77.
两边都除以-7,得:
x=11.
随堂练习
解下列方程:
(1) 5(x+2)=2(5x-1);
(2) (x+1)-2(x-1)=1-3x;
(3) 2(x-2)-(4x-1)=3(1-x).
去括号得:5x+10=10x-2,
移项,得:5x-10x=-2-10,即-5x=-12.
两边都除以-5,得:
去括号得:x+1-2x+2=1-3x,即-x+3=1-3x.
移项,得:-x+3x=1-3,即2x=-2.
两边都除以2,得:x=-1.
去括号得:2x-4-4x+1=3-3x,即-2x-3=3-3x.
移项,得:-2x+3x=3+3,即x=6.
例4 当x取何值时,代数式2x+3的值与3(1-x)的值
互为相反数?
例题精析
解:依题意得:
(2x+3)+3(1-x)=0,
去括号得:
2x+3+3-3x=0,
即 -x+6=0.
移项,得:
x=6.
∴ 当x=6时,代数式2x+3的值与3(1-x)的值互为
相反数.
例5 当x取何值时,代数式5(2-x)的值比代数式
9(2x-1)的值小4?
解:依题意得:
5(2-x)-9(2x-1)=-4,
去括号得:
10-5x-18x+9=-4,
即 -23x+19=-4.
移项得: -23x=-4-19,
即 -23x=-23.
两边都除以-23,得:
x=1.
∴当x=1时,代数式5(2-x)的值比代数式9(2x-1)的值小4.
随堂练习
1.当x取何值时,代数式3(2-x)的值与2(3+x)的值
相等?
解:依题意得:
3(2-x)=2(3+x),
去括号得:
6-3x=6+2x,
移项得: -3x-2x=6-6,
即 -5x=0.
两边都除以-5,得:
x=0.
∴当x=0时,代数式3(2-x)的值与2(3+x)的值相等.
2. 当y取何值时,代数式2(3y+4)的值比代数式
5(2y-7)的值大3?
随堂练习
解:依题意得:
2(3y+4)-5(2y-7)=3,
去括号得:
6y+8-10y+35=3,
即 -4y+43=3.
移项得: -4y=3-43,
即 -4y=-40.
两边都除以-4,得:
y=10.
∴当y=10时,代数式2(3y+4)的值比代数式5(2y-7)的值大3.
一、一元一次方程的概念:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数都是1的方程.
概念要点:
(1)只含有一个未知数;
(2)含有未知数的式子都是整式;
(3)未知数的次数都是1.
(注意:未知数的系数不能为0)
(整式包括多项式和多项式)
(未知数的次数只能等于1)
课堂小结
二、解含有括号的一元一次方程的步骤:
1.去括号;
2.合并同类项;
3.移项;
4.系数化为1.
作 业
1.当x取何值时,代数式12-3(6-x)的值与5(4-x)的
值互为相反数?
2.当y取何值时,代数式2(3y-1)的值比3(y+1)的值
大4?
解:依题意得: 12-3(6-x)+5(4-x)=0,
去括号得: 12-18+3x+20-5x=0,即-2x+14=0.
移项得:-2x=-14.
两边都除以-2,得:x=7.
解:依题意得: 2(3y-1)-3(y+1)=4,
去括号得: 6y-2-3y-3=4,即3y-5=4.
移项得:3y=9.
两边都除以3,得:y=3.
作业与课外学习任务
1.练习作业:学习检测P7-9 第1至20题
书面课本P14 习题6.2.2 1
2.课外学习任务:
预习课本P10 6.2.2 解一元一次方程 例5
(含分母的一元一次方程的解法)
教学反馈:
作业存在的主要问题:
