华东师大版七年级下册数学课件:6.2.1 等式的性质与方程的简单变形1(共38张)
文档属性
| 名称 | 华东师大版七年级下册数学课件:6.2.1 等式的性质与方程的简单变形1(共38张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览






文档简介
第6章 一元一次方程
6.2 解一元一次方程
1. 等式的性质与方程的简单变形
教学目标
教学重点与难点
重点:方程的两种变形.
难点:由具体实例抽象出方程的两种变形.
1.通过实践以及生活中的问题,直观感受方程的
简单变形。?
2.通过天平实验,让学生在观察、思考的基础上
归纳出方程的两种变形,并能利用它们将简单的方程变形以求出未知数的值
温故夯基
1.方程的定义:含有未知数的等式叫做方程.
2.方程的解是指使方程左右两边相等的未知数的值.
3.检验一个数是否是方程的解方法:
将这个数分别代入原方程的左边和右边计算代数式的值,如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
4.列方程的思考途径:
(1)把题中的未知量用字母表示;
(2)把表示数量关系的语言转换为含字母的算式;
(3)根据等量关系,列出方程.
巩固练习
√
×
×
√
√
√
√
×
C
2.下列说法不正确的个数是( ).
①等式都是方程 ②方程都是等式
③不是方程的就不是等式
④未知数的值就是方程的解
A.3个 B.2个 C.1个 D.0个
×
×
×
√
A
1.下列各式:①2x-3=5;②4+9=13;③5y+9;
④2x+4y=0;⑤2x2+3x=1;⑥2x2-6x-1;
⑦|x|+1=3; ⑧ ,是方程的有( ).
A.①②④⑤⑧ B.①②⑤⑦⑧
C.①④⑤⑦⑧ D.8个都是
B
4.甲、乙两数的和为10,并且甲比乙大3,
求甲、乙两数.下面所列方程正确的是( ).
A.设乙数为x,则(x+3)+x=10
B.设乙数为x,则(x-3)+x=10
C.设甲数为x,则(x+3)+x=10
D.设乙数为x,则x-3=10
A
5.x= -2是方程x+a=7的解,则 a的值是( ).
A.-9 B.7 C.- 7 D.9
D
3.下列各方程后面括号里的数是该方程的解的是( )
A.3x+4= -13{-4} B. x-1=5{9}
C. 6-2x= {-1 } D. 5-y=-16{ }
6.方程2018x-m=2019的解是x=1,则m=____.
-1
7.已知y=1是方程my=y-3的解,
则m2-3m+1的值是 .
11
8.李红买了6支钢笔,付了50元,找回14元,
设每支钢笔的价格为x元,根据题意可列方程
为_____________.
6x+14=50
9. 3个连续偶数的和是30,设最小的偶数为y,
则可列方程为______________________.
y+(y+2)+(y+4)=30
10.某校七年级组织学生去科技馆参观,共租用9辆
大客车,每辆车有座位60个,老师共去20人.若该年级
的男生比女生多30人,刚好每人都有座位.
设该校女生有x人,则可列出方程为 .
x+(x+30)+20=60×9
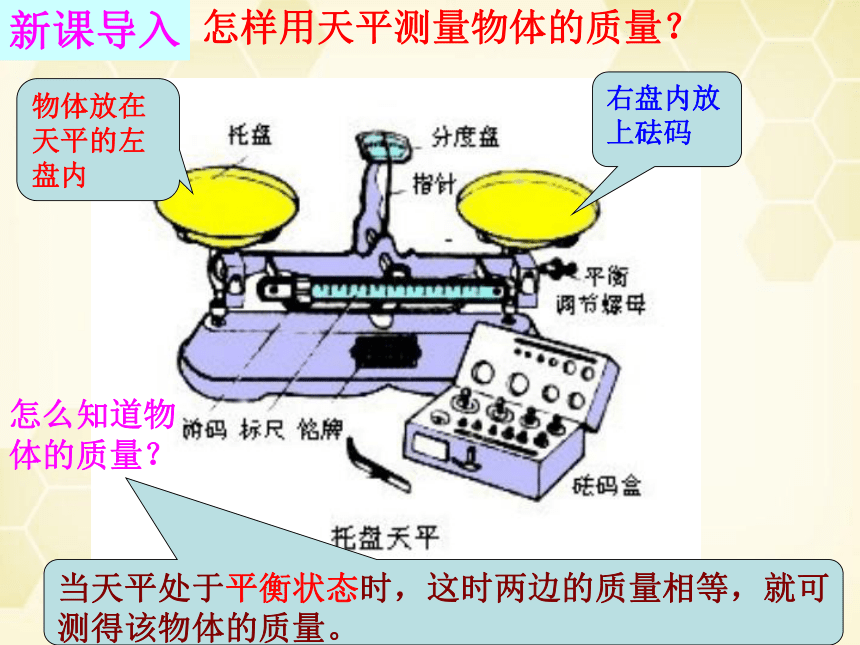
怎样用天平测量物体的质量?
物体放在天平的左盘内
右盘内放
上砝码
怎么知道物体的质量?
当天平处于平衡状态时,这时两边的质量相等,就可测得该物体的质量。
新课导入
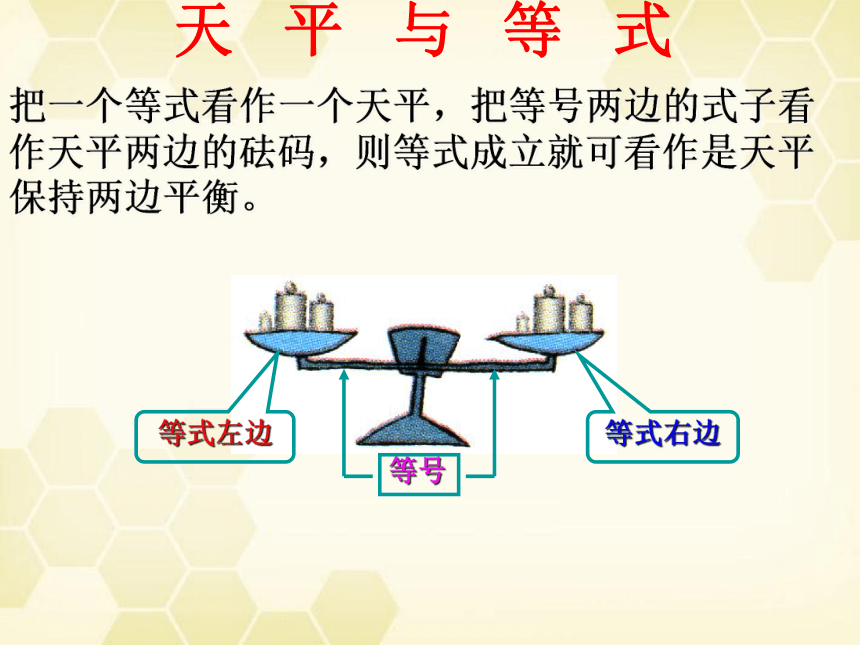
天 平 与 等 式
等式左边
等式右边
等号
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
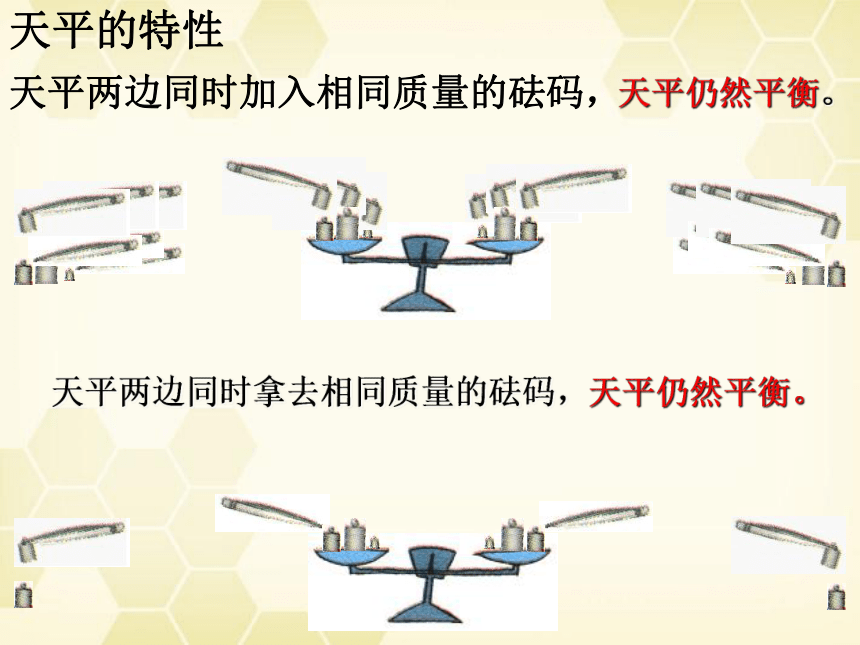
天平两边同时加入相同质量的砝码,
天平仍然平衡。
天平两边同时拿去相同质量的砝码,
天平仍然平衡。
天平的特性
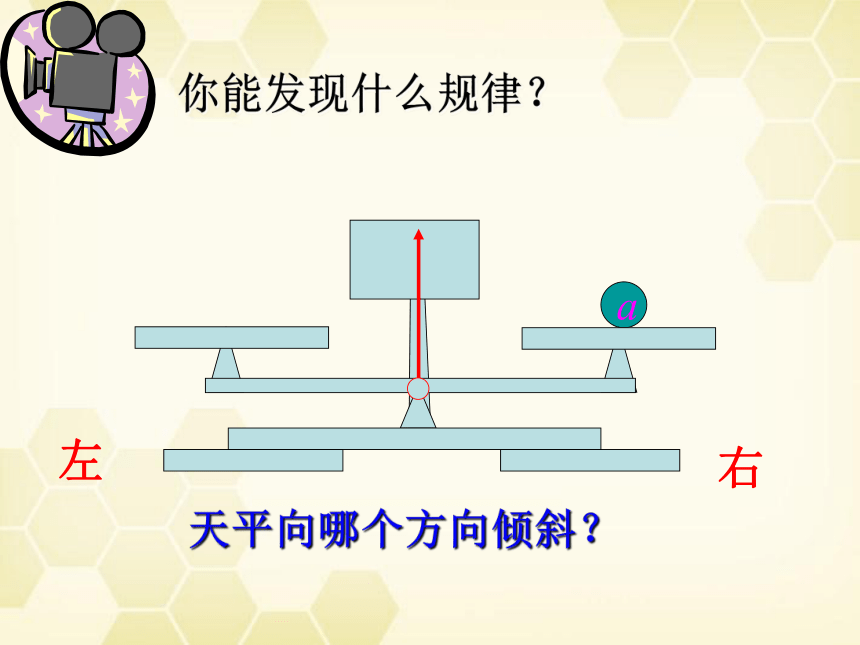
a
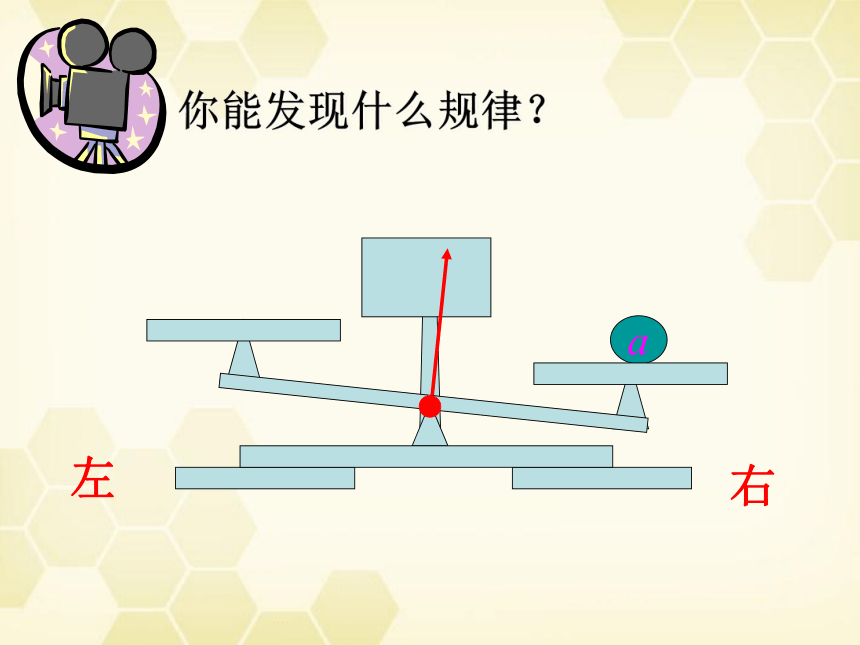
你能发现什么规律?
右
左
天平向哪个方向倾斜?
a
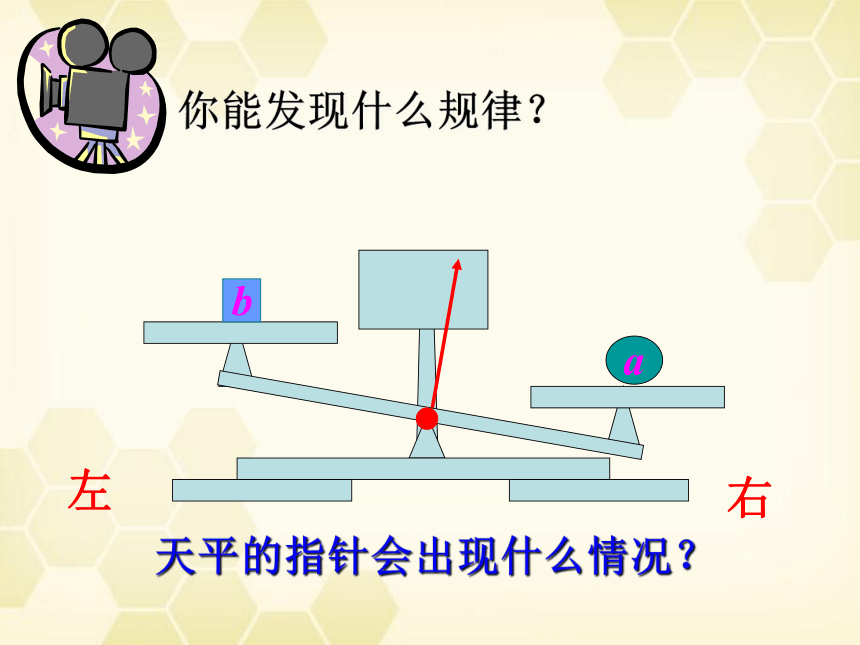
你能发现什么规律?
右
左
b
右
左
你能发现什么规律?
a
天平的指针会出现什么情况?
a = b
右
左
你能发现什么规律?
a
b
天平的指针又回到中间,说明什么?
c
右
左
你能发现什么规律?
a = b
a
b
天平的指针会出现什么情况?
右
左
你能发现什么规律?
a = b
a
b
c
右
左
你能发现什么规律?
a = b
a
b
c
c
天平的指针又会出现什么情况?
a+c b+c
=
右
左
你能发现什么规律?
a
b
c
c
a = b
c
c
a = b
a
b
右
左
你能发现什么规律?
c
a = b
a
b
右
左
你能发现什么规律?
c
a = b
a
b
右
左
你能发现什么规律?
b
a
右
左
你能发现什么规律?
a = b
a = b
a-c b-c
=
b
a
右
左
你能发现什么规律?
b
a
a = b
右
左
你能发现什么规律?
b
a
a = b
右
左
a
b
2a = 2b
你能发现什么规律?
b
a
a = b
右
左
b
b
a
a
3a = 3b
你能发现什么规律?
b
a
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
你能发现什么规律?
b
a
a = b
右
左
你能发现什么规律?
学习新知
等式的基本性质
1.等式两边都加上(或都减去)同一个数或同一个
整式,所得结果仍是等式.
如果a=b,那么a+c=b+c,a-c=b-c.
2.等式两边都乘以(或都除以)同一个数(除数
不能为0),所得结果仍是等式.
如果a=b,那么ac=bc, .
【等式性质2】
【等式性质1】
? 注意 ?
1.等式两边都要参加运算,并且是作同一种
运算。
2.等式两边加或减,乘或除以的数一定是同
一个数或同一个式子。
3.等式两边不能都除以0,即0不能作除数或
分母.
要点说明
(1)如果x-5=7,那么x-5+5= ,
根据 .
等式的基本性质1,在等式两边都加上5
7+5
例1
例题精析
(2)如果4x=3x-4,那么4x-3x= ,
根据 .
3x-4-3x
等式的基本性质1,在等式两边都减去3x
(3)如果 ,那么 = ,
根据 .
2×2
等式的基本性质2,在等式两边都乘以2
(4)如果4x= -12y,那么x= ,
根据 .
-3y
等式性质2,在等式两边都除以4
(5)如果-0.2x= 6,那么x= ,
根据 .
-30
等式的基本性质2,在等式两边都乘以-5或
除以-0.2
例2 下列变形符合等式性质的是( ).
A. 如果2x-3=7,那么2x=7-3.
B. 如果3x-2=1,那么3x=1-2.
C. 如果-2x=5,那么x=5+2.
D. 如果 ,那么x=-3.
例题精析
D
例3 依据等式性质进行变形,用得不正确的是( ).
D
例4 判断下列说法是否成立,并说明理由:
( )
( )
( )
.
(因为x可能等于0)
(等量代换)
(对称性)
例题精析
随堂练习
1.回答下列问题:
(1)由a=b能不能得到a-2=b-2?为什么?
(2)由m=n能不能得到 ?为什么?
(3)由2a=6b能不能得到a=3b?为什么?
(4)由 能不能得到3x=2y?为什么?
能得到,
通过等式两边都减去2得到.
能得到,
能得到,
能得到,
通过等式两边都除以-3得到.
通过等式两边都除以2得到.
通过等式两边都乘以6得到.
2.填空,使所得结果仍是等式,并说明是根据
哪一条等式性质得到的:
随堂练习
(1)如果x-2=5,那么x=5+ ;
(2)如果3x=10-2x,那么3x+ =10;
(3)如果2x=7,那么x= ;
(4)如果 ,那么x-1= .
根据等式的基本性质1,在等式两边都加上2得到的.
根据等式的基本性质1,在等式两边都加上2x得到的.
根据等式的基本性质2,在等式两边都除以2得到的.
根据等式的基本性质2,在等式两边都乘以2得到的.
等式的基本性质
1.等式两边都加上(或都减去)同一个数或同一个
整式,所得结果仍是等式.
如果a=b,那么a+c=b+c,a-c=b-c.
2.等式两边都乘以(或都除以)同一个数(除数
不能为0),所得结果仍是等式.
如果a=b,那么ac=bc, .
课堂小结
1.等式两边都要参加运算,并且是作同一种运算。
2.等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3.等式两边不能都除以0,即0不能作除数或分母.
注意事项
作业与课外学习任务
1.练习作业:学习检测P4-5 第1至17题
书面课本P9 习题6.2.1
2.课外学习任务:
预习课本P5 6.2.1 等式的性质与方程的简单变形
方程的变形规则
教学反馈:
作业存在的主要问题:
6.2 解一元一次方程
1. 等式的性质与方程的简单变形
教学目标
教学重点与难点
重点:方程的两种变形.
难点:由具体实例抽象出方程的两种变形.
1.通过实践以及生活中的问题,直观感受方程的
简单变形。?
2.通过天平实验,让学生在观察、思考的基础上
归纳出方程的两种变形,并能利用它们将简单的方程变形以求出未知数的值
温故夯基
1.方程的定义:含有未知数的等式叫做方程.
2.方程的解是指使方程左右两边相等的未知数的值.
3.检验一个数是否是方程的解方法:
将这个数分别代入原方程的左边和右边计算代数式的值,如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
4.列方程的思考途径:
(1)把题中的未知量用字母表示;
(2)把表示数量关系的语言转换为含字母的算式;
(3)根据等量关系,列出方程.
巩固练习
√
×
×
√
√
√
√
×
C
2.下列说法不正确的个数是( ).
①等式都是方程 ②方程都是等式
③不是方程的就不是等式
④未知数的值就是方程的解
A.3个 B.2个 C.1个 D.0个
×
×
×
√
A
1.下列各式:①2x-3=5;②4+9=13;③5y+9;
④2x+4y=0;⑤2x2+3x=1;⑥2x2-6x-1;
⑦|x|+1=3; ⑧ ,是方程的有( ).
A.①②④⑤⑧ B.①②⑤⑦⑧
C.①④⑤⑦⑧ D.8个都是
B
4.甲、乙两数的和为10,并且甲比乙大3,
求甲、乙两数.下面所列方程正确的是( ).
A.设乙数为x,则(x+3)+x=10
B.设乙数为x,则(x-3)+x=10
C.设甲数为x,则(x+3)+x=10
D.设乙数为x,则x-3=10
A
5.x= -2是方程x+a=7的解,则 a的值是( ).
A.-9 B.7 C.- 7 D.9
D
3.下列各方程后面括号里的数是该方程的解的是( )
A.3x+4= -13{-4} B. x-1=5{9}
C. 6-2x= {-1 } D. 5-y=-16{ }
6.方程2018x-m=2019的解是x=1,则m=____.
-1
7.已知y=1是方程my=y-3的解,
则m2-3m+1的值是 .
11
8.李红买了6支钢笔,付了50元,找回14元,
设每支钢笔的价格为x元,根据题意可列方程
为_____________.
6x+14=50
9. 3个连续偶数的和是30,设最小的偶数为y,
则可列方程为______________________.
y+(y+2)+(y+4)=30
10.某校七年级组织学生去科技馆参观,共租用9辆
大客车,每辆车有座位60个,老师共去20人.若该年级
的男生比女生多30人,刚好每人都有座位.
设该校女生有x人,则可列出方程为 .
x+(x+30)+20=60×9
怎样用天平测量物体的质量?
物体放在天平的左盘内
右盘内放
上砝码
怎么知道物体的质量?
当天平处于平衡状态时,这时两边的质量相等,就可测得该物体的质量。
新课导入
天 平 与 等 式
等式左边
等式右边
等号
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
天平两边同时加入相同质量的砝码,
天平仍然平衡。
天平两边同时拿去相同质量的砝码,
天平仍然平衡。
天平的特性
a
你能发现什么规律?
右
左
天平向哪个方向倾斜?
a
你能发现什么规律?
右
左
b
右
左
你能发现什么规律?
a
天平的指针会出现什么情况?
a = b
右
左
你能发现什么规律?
a
b
天平的指针又回到中间,说明什么?
c
右
左
你能发现什么规律?
a = b
a
b
天平的指针会出现什么情况?
右
左
你能发现什么规律?
a = b
a
b
c
右
左
你能发现什么规律?
a = b
a
b
c
c
天平的指针又会出现什么情况?
a+c b+c
=
右
左
你能发现什么规律?
a
b
c
c
a = b
c
c
a = b
a
b
右
左
你能发现什么规律?
c
a = b
a
b
右
左
你能发现什么规律?
c
a = b
a
b
右
左
你能发现什么规律?
b
a
右
左
你能发现什么规律?
a = b
a = b
a-c b-c
=
b
a
右
左
你能发现什么规律?
b
a
a = b
右
左
你能发现什么规律?
b
a
a = b
右
左
a
b
2a = 2b
你能发现什么规律?
b
a
a = b
右
左
b
b
a
a
3a = 3b
你能发现什么规律?
b
a
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
你能发现什么规律?
b
a
a = b
右
左
你能发现什么规律?
学习新知
等式的基本性质
1.等式两边都加上(或都减去)同一个数或同一个
整式,所得结果仍是等式.
如果a=b,那么a+c=b+c,a-c=b-c.
2.等式两边都乘以(或都除以)同一个数(除数
不能为0),所得结果仍是等式.
如果a=b,那么ac=bc, .
【等式性质2】
【等式性质1】
? 注意 ?
1.等式两边都要参加运算,并且是作同一种
运算。
2.等式两边加或减,乘或除以的数一定是同
一个数或同一个式子。
3.等式两边不能都除以0,即0不能作除数或
分母.
要点说明
(1)如果x-5=7,那么x-5+5= ,
根据 .
等式的基本性质1,在等式两边都加上5
7+5
例1
例题精析
(2)如果4x=3x-4,那么4x-3x= ,
根据 .
3x-4-3x
等式的基本性质1,在等式两边都减去3x
(3)如果 ,那么 = ,
根据 .
2×2
等式的基本性质2,在等式两边都乘以2
(4)如果4x= -12y,那么x= ,
根据 .
-3y
等式性质2,在等式两边都除以4
(5)如果-0.2x= 6,那么x= ,
根据 .
-30
等式的基本性质2,在等式两边都乘以-5或
除以-0.2
例2 下列变形符合等式性质的是( ).
A. 如果2x-3=7,那么2x=7-3.
B. 如果3x-2=1,那么3x=1-2.
C. 如果-2x=5,那么x=5+2.
D. 如果 ,那么x=-3.
例题精析
D
例3 依据等式性质进行变形,用得不正确的是( ).
D
例4 判断下列说法是否成立,并说明理由:
( )
( )
( )
.
(因为x可能等于0)
(等量代换)
(对称性)
例题精析
随堂练习
1.回答下列问题:
(1)由a=b能不能得到a-2=b-2?为什么?
(2)由m=n能不能得到 ?为什么?
(3)由2a=6b能不能得到a=3b?为什么?
(4)由 能不能得到3x=2y?为什么?
能得到,
通过等式两边都减去2得到.
能得到,
能得到,
能得到,
通过等式两边都除以-3得到.
通过等式两边都除以2得到.
通过等式两边都乘以6得到.
2.填空,使所得结果仍是等式,并说明是根据
哪一条等式性质得到的:
随堂练习
(1)如果x-2=5,那么x=5+ ;
(2)如果3x=10-2x,那么3x+ =10;
(3)如果2x=7,那么x= ;
(4)如果 ,那么x-1= .
根据等式的基本性质1,在等式两边都加上2得到的.
根据等式的基本性质1,在等式两边都加上2x得到的.
根据等式的基本性质2,在等式两边都除以2得到的.
根据等式的基本性质2,在等式两边都乘以2得到的.
等式的基本性质
1.等式两边都加上(或都减去)同一个数或同一个
整式,所得结果仍是等式.
如果a=b,那么a+c=b+c,a-c=b-c.
2.等式两边都乘以(或都除以)同一个数(除数
不能为0),所得结果仍是等式.
如果a=b,那么ac=bc, .
课堂小结
1.等式两边都要参加运算,并且是作同一种运算。
2.等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3.等式两边不能都除以0,即0不能作除数或分母.
注意事项
作业与课外学习任务
1.练习作业:学习检测P4-5 第1至17题
书面课本P9 习题6.2.1
2.课外学习任务:
预习课本P5 6.2.1 等式的性质与方程的简单变形
方程的变形规则
教学反馈:
作业存在的主要问题:
