华东师大版七年级下册数学课件:6.1 从实际问题到方程(共21张)
文档属性
| 名称 | 华东师大版七年级下册数学课件:6.1 从实际问题到方程(共21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览








文档简介
第6章 一元一次方程
6.1 从实际问题到方程
教学目标
教学重点与难点
重点:懂得方程,方程解的概念,了解检验方程的解的方法.
难点:掌握方程是刻画现实世界的一个有效的
数学模型.
1.了解方程、方程的解的概念,知道检验方程的
解的方法.
2.能根据题意建立数学模型,简单列出的方程.
3.懂得方程是刻画现实世界的一个有效的数学模型.
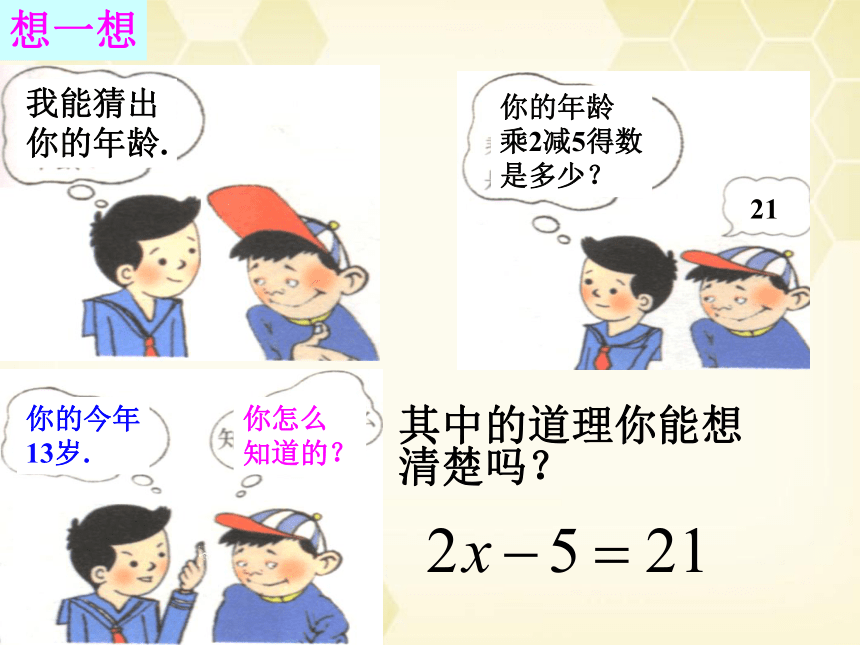
其中的道理你能想清楚吗?
想一想
我能猜出
你的年龄.
你的年龄
乘2减5得数
是多少?
21
你的今年
13岁.
你怎么
知道的?
问题1 某学校七年级328名师生乘车外出春游,已有两辆校车共可乘坐64人,如果租用客车,每辆可乘44人,那么还要租多少辆客车?
问题引入
这个问题是我们在生活中碰到的实际问题,
你能利用所学的知识来解决吗?
设需租用客车 辆,共可乘坐 人,
加上乘坐校车的64人,就是全体328人.可得
你会解这个方程吗?试一试.
问题1 某校七年级328名师生乘车外出春游,已有两辆校车共可乘坐64人,如果租用客车,每辆可乘44人,那么还要租多少辆客车?
这是一个利用方程解决的实际问题,基本思路是先分析问题中的数量关系,包括已知数和未知数以及包括题目中所含有的等量关系。
如上题中的等量关系为:
乘坐校车的人数+乘坐客车的人数=师生总人数
然后用字母表示未知数(即设元)列出需要的代数式如44x,从而根据等量关系列出方程。
含有未知数的等式叫做方程.
问题2 在课外活动中,陈老师发现同学们的年龄大多是13岁.就问同学:“我今年45岁,经过几年后你们的年龄正好是我年龄的三分之一?”
一年后年龄:老师 46岁 同学 14岁
不是老师的
二年后年龄:老师 47岁 同学 15岁
也不是老师的
三年后年龄:老师 48岁 同学 16岁
恰好是老师的
你会列方程来解决这个问题吗?
问题2 在课外活动中,陈老师发现同学们的年龄大多是13岁.就问同学:“我今年45岁,经过几年后你们的年龄正好是我年龄的三分之一?”
如果设经过x年同学的年龄是老师的三分之一,
那么x年后同学的年龄为 岁,
老师的年龄是______岁,所以得到等式:
(13+x)
(45+x)
通过刚才不用方程的分析方法可以启发我们:
只要将x=1,2,3,4等等代入方程的左右两边,
使得两边相等的那个数就是方程的解,这里x=3
是方程的解.
方程的解是指使方程左右两边相等的未知数的值.
如何检验一个数是否是某方程的解?
方法是:
将这个数分别代入原方程的左边和右边计算代数式的值,如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
例题精析
例1 以下各方程后面的括号内分别给出了一组数,
从中找出方程的解.
(1)6x+2=14(0,1,2,3);
(2)10=3x+1(0,1,2,3);
(3)2x-4=12(4,8,12);
(4)3= x-1(3,6,9).
x=2
x=3
x=8
x=6
例2 根据题意设未知数,并列出方程(不必求解):
(1)用12元钱买3个笔记本,找回1.2元,每个笔记本
多少钱?
(2)甲、乙两数的和为10,且甲比乙大2,
求甲、乙两数.
解:设每个笔记本x元,
根据题意,得: 3 x+ 1.2=12.
解:设乙数为x,则甲数为(x+2),
根据题意,得: (x+ 2)+x=10.
解:设甲数为x,则乙数为(x-2),
根据题意,得: x+(x-2)=10.
(1)把题中的未知量用字母表示;
(2)把表示数量关系的语言转换为含字母的算式;
(3)根据等量关系,列出方程.
列方程的思考途径:
归纳总结
(1)某班原分成两个小组活动,第一组26人,第二组22人,根据学校活动器材的数量,要将第一组人数调整为第二组人数的一半,应从第一组调多少人到第二组去?
1.根据题意设未知数,并列出方程(不必求解):
第一组
第二组
原来
调整后
26
22
解:设应从第一组调x人到第二组去,
26-x
22+x
随堂练习
根据题意,得:
(2)师徒两人铺设一条长186米的地下电缆,师傅每小时铺设18米,徒弟每小时铺设12米.师傅先开始工作,2个小时后徒弟在另一端开始铺设,那么师徒两人还需一起工作多长时间才能完成铺设任务?
分析:(师傅铺设的长度+徒弟铺设的长度=总长度)
解:设师徒两人还需一起工作x 小时才能完成铺设任务,
根据题意,得:
12x+18(2+x)=186.
(3)小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得到的本利和为3243元.请你帮小明算一算这种储蓄 的年利率.
3000
+
=3243
(本利和是指本金与利息的和)
(年利息=本金×年利率×年数)
解:设这种储蓄 的年利率是x ,
根据题意,得:
2.检验下列各括号内的数是不是它前面方程的解。
(1)x-3(x+2)=6+x (x=3,x=-4);
(2)44x+64=328 (x=5,x=6);
(3)2.5x-0.5x=3.3x-1.2x (x=47,x=0,x=3500).
x=-4
x=6
x=0
3.判断题:
(1)x=2是方程x-10=-4的解-----------------( )
(2)x=1与x=-1都是方程x2-1=0的解-------( )
(3)方程12(x-3)-1=2x+3的解是x=-4------ ( )
×
√
×
4.已知x=2是方程2(x-3)+1=x+m的解,则m=( ).
A . 3 B. 2 C .-3 D . -2
C
丢番图的墓志铭
墓中,长眠着一个伟大的人物——丢番图.
他的一生的六分之一时光,是童年时代;又度过了十二分之一岁月后,他满脸长出了胡须;再过了七分之一年月时,举行了花烛盛典;婚后五年,得一贵子.
可是不幸的孩子,他仅仅活了父亲的半生时光,就离开了人间.
从此,作为父亲的丢番图,在悲伤中度过了四年后,结束了自己的一生.
你知道丢番图活了多少岁吗?
如果设的年龄是x,由题意,得:
+
+
+
+
+
=
你会解这个
方程吗?
通过下节课的学习,你就会了!
课堂小结
1.方程的定义:含有未知数的等式叫做方程.
2.方程的解是指使方程左右两边相等的未知数的值.
3.检验一个数是否是方程的解方法:
将这个数分别代入原方程的左边和右边计算代数式的值,如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
(1)把题中的未知量用字母表示;
(2)把表示数量关系的语言转换为含字母的算式;
(3)根据等量关系,列出方程.
4.列方程的思考途径:
作业与课外学习任务
1.练习作业:学习检测P1-3 第1至19题
书面课本P4 习题6.1 1,3
2.课外学习任务:
预习课本P4 6.2.1 等式的性质与方程的简单变形
教学反馈:
作业存在的主要问题:
6.1 从实际问题到方程
教学目标
教学重点与难点
重点:懂得方程,方程解的概念,了解检验方程的解的方法.
难点:掌握方程是刻画现实世界的一个有效的
数学模型.
1.了解方程、方程的解的概念,知道检验方程的
解的方法.
2.能根据题意建立数学模型,简单列出的方程.
3.懂得方程是刻画现实世界的一个有效的数学模型.
其中的道理你能想清楚吗?
想一想
我能猜出
你的年龄.
你的年龄
乘2减5得数
是多少?
21
你的今年
13岁.
你怎么
知道的?
问题1 某学校七年级328名师生乘车外出春游,已有两辆校车共可乘坐64人,如果租用客车,每辆可乘44人,那么还要租多少辆客车?
问题引入
这个问题是我们在生活中碰到的实际问题,
你能利用所学的知识来解决吗?
设需租用客车 辆,共可乘坐 人,
加上乘坐校车的64人,就是全体328人.可得
你会解这个方程吗?试一试.
问题1 某校七年级328名师生乘车外出春游,已有两辆校车共可乘坐64人,如果租用客车,每辆可乘44人,那么还要租多少辆客车?
这是一个利用方程解决的实际问题,基本思路是先分析问题中的数量关系,包括已知数和未知数以及包括题目中所含有的等量关系。
如上题中的等量关系为:
乘坐校车的人数+乘坐客车的人数=师生总人数
然后用字母表示未知数(即设元)列出需要的代数式如44x,从而根据等量关系列出方程。
含有未知数的等式叫做方程.
问题2 在课外活动中,陈老师发现同学们的年龄大多是13岁.就问同学:“我今年45岁,经过几年后你们的年龄正好是我年龄的三分之一?”
一年后年龄:老师 46岁 同学 14岁
不是老师的
二年后年龄:老师 47岁 同学 15岁
也不是老师的
三年后年龄:老师 48岁 同学 16岁
恰好是老师的
你会列方程来解决这个问题吗?
问题2 在课外活动中,陈老师发现同学们的年龄大多是13岁.就问同学:“我今年45岁,经过几年后你们的年龄正好是我年龄的三分之一?”
如果设经过x年同学的年龄是老师的三分之一,
那么x年后同学的年龄为 岁,
老师的年龄是______岁,所以得到等式:
(13+x)
(45+x)
通过刚才不用方程的分析方法可以启发我们:
只要将x=1,2,3,4等等代入方程的左右两边,
使得两边相等的那个数就是方程的解,这里x=3
是方程的解.
方程的解是指使方程左右两边相等的未知数的值.
如何检验一个数是否是某方程的解?
方法是:
将这个数分别代入原方程的左边和右边计算代数式的值,如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
例题精析
例1 以下各方程后面的括号内分别给出了一组数,
从中找出方程的解.
(1)6x+2=14(0,1,2,3);
(2)10=3x+1(0,1,2,3);
(3)2x-4=12(4,8,12);
(4)3= x-1(3,6,9).
x=2
x=3
x=8
x=6
例2 根据题意设未知数,并列出方程(不必求解):
(1)用12元钱买3个笔记本,找回1.2元,每个笔记本
多少钱?
(2)甲、乙两数的和为10,且甲比乙大2,
求甲、乙两数.
解:设每个笔记本x元,
根据题意,得: 3 x+ 1.2=12.
解:设乙数为x,则甲数为(x+2),
根据题意,得: (x+ 2)+x=10.
解:设甲数为x,则乙数为(x-2),
根据题意,得: x+(x-2)=10.
(1)把题中的未知量用字母表示;
(2)把表示数量关系的语言转换为含字母的算式;
(3)根据等量关系,列出方程.
列方程的思考途径:
归纳总结
(1)某班原分成两个小组活动,第一组26人,第二组22人,根据学校活动器材的数量,要将第一组人数调整为第二组人数的一半,应从第一组调多少人到第二组去?
1.根据题意设未知数,并列出方程(不必求解):
第一组
第二组
原来
调整后
26
22
解:设应从第一组调x人到第二组去,
26-x
22+x
随堂练习
根据题意,得:
(2)师徒两人铺设一条长186米的地下电缆,师傅每小时铺设18米,徒弟每小时铺设12米.师傅先开始工作,2个小时后徒弟在另一端开始铺设,那么师徒两人还需一起工作多长时间才能完成铺设任务?
分析:(师傅铺设的长度+徒弟铺设的长度=总长度)
解:设师徒两人还需一起工作x 小时才能完成铺设任务,
根据题意,得:
12x+18(2+x)=186.
(3)小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得到的本利和为3243元.请你帮小明算一算这种储蓄 的年利率.
3000
+
=3243
(本利和是指本金与利息的和)
(年利息=本金×年利率×年数)
解:设这种储蓄 的年利率是x ,
根据题意,得:
2.检验下列各括号内的数是不是它前面方程的解。
(1)x-3(x+2)=6+x (x=3,x=-4);
(2)44x+64=328 (x=5,x=6);
(3)2.5x-0.5x=3.3x-1.2x (x=47,x=0,x=3500).
x=-4
x=6
x=0
3.判断题:
(1)x=2是方程x-10=-4的解-----------------( )
(2)x=1与x=-1都是方程x2-1=0的解-------( )
(3)方程12(x-3)-1=2x+3的解是x=-4------ ( )
×
√
×
4.已知x=2是方程2(x-3)+1=x+m的解,则m=( ).
A . 3 B. 2 C .-3 D . -2
C
丢番图的墓志铭
墓中,长眠着一个伟大的人物——丢番图.
他的一生的六分之一时光,是童年时代;又度过了十二分之一岁月后,他满脸长出了胡须;再过了七分之一年月时,举行了花烛盛典;婚后五年,得一贵子.
可是不幸的孩子,他仅仅活了父亲的半生时光,就离开了人间.
从此,作为父亲的丢番图,在悲伤中度过了四年后,结束了自己的一生.
你知道丢番图活了多少岁吗?
如果设的年龄是x,由题意,得:
+
+
+
+
+
=
你会解这个
方程吗?
通过下节课的学习,你就会了!
课堂小结
1.方程的定义:含有未知数的等式叫做方程.
2.方程的解是指使方程左右两边相等的未知数的值.
3.检验一个数是否是方程的解方法:
将这个数分别代入原方程的左边和右边计算代数式的值,如果左边=右边,那么这个数就是这个方程的解;如果左边≠右边,那么这个数就不是这个方程的解.
(1)把题中的未知量用字母表示;
(2)把表示数量关系的语言转换为含字母的算式;
(3)根据等量关系,列出方程.
4.列方程的思考途径:
作业与课外学习任务
1.练习作业:学习检测P1-3 第1至19题
书面课本P4 习题6.1 1,3
2.课外学习任务:
预习课本P4 6.2.1 等式的性质与方程的简单变形
教学反馈:
作业存在的主要问题:
