7.3二次根式的加减 课件(共24张PPT)
文档属性
| 名称 | 7.3二次根式的加减 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 19:16:01 | ||
图片预览






文档简介
第七章 二次根式
3 二次根式的加减
知识点一 同类二次根式
内容
举例
概念
特别提醒
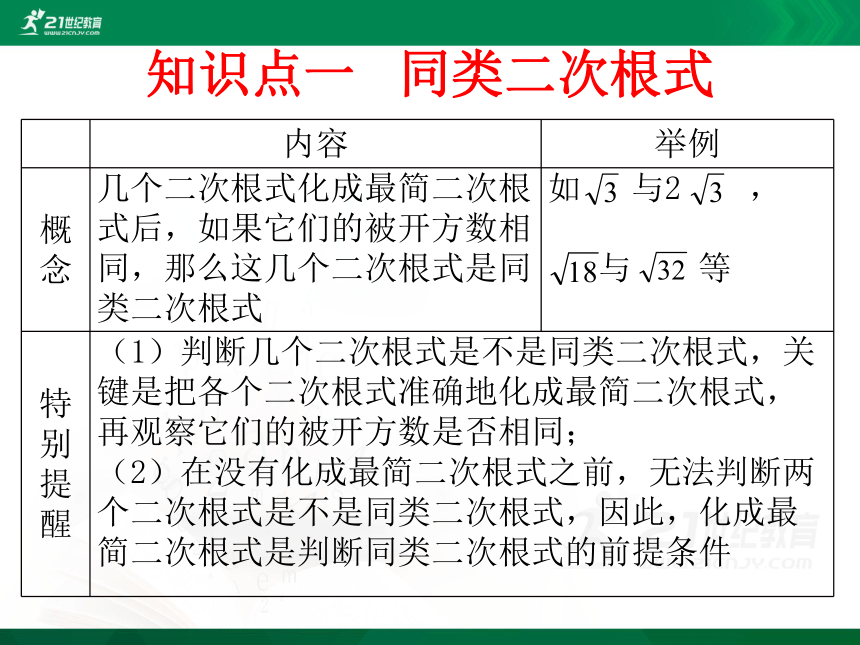
知识点一 同类二次根式
内容
举例
概念
几个二次根式化成最简二次根式后,如果它们的被开方数相同,那么这几个二次根式是同类二次根式
如 与2 ,
与 等
特别提醒
(1)判断几个二次根式是不是同类二次根式,关键是把各个二次根式准确地化成最简二次根式,再观察它们的被开方数是否相同;
(2)在没有化成最简二次根式之前,无法判断两个二次根式是不是同类二次根式,因此,化成最简二次根式是判断同类二次根式的前提条件
例1 以下二次根式:① ;② ;③ ;④ .
与 是同类二次根式的是( )
A.①和② B.②和③ C.①和④ D.③和④
例1 以下二次根式:① ;② ;③ ;④ .
与 是同类二次根式的是( )
A.①和② B.②和③ C.①和④ D.③和④
解析 ∵ =2 , =2, = , =3 ,
∴与 是同类二次根式的是①和④.
答案 C
例1 以下二次根式:① ;② ;③ ;④ .
与 是同类二次根式的是( )
A.①和② B.②和③ C.①和④ D.③和④
解析 ∵ =2 , =2, = , =3 ,
∴与 是同类二次根式的是①和④.
答案 C
温馨提示 要判断几个二次根式是不是同类二次根式,不要被表面上的被开方数迷惑,要把它化成最简二次根式后再作出判断.
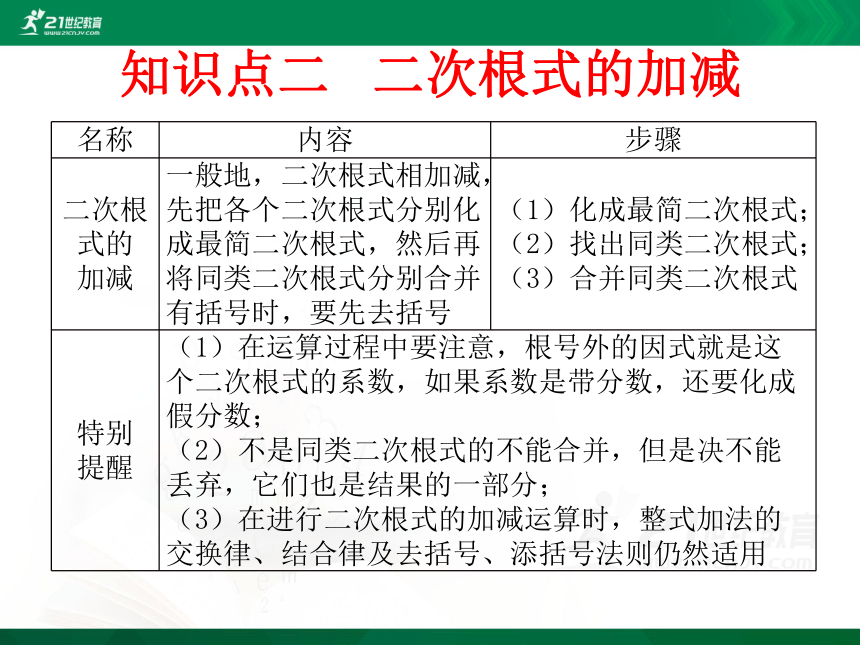
知识点二 二次根式的加减
名称
内容
步骤
二次根式的
加减
特别
提醒
知识点二 二次根式的加减
名称
内容
步骤
二次根式的
加减
一般地,二次根式相加减,先把各个二次根式分别化成最简二次根式,然后再将同类二次根式分别合并有括号时,要先去括号
(1)化成最简二次根式;
(2)找出同类二次根式;
(3)合并同类二次根式
特别
提醒
(1)在运算过程中要注意,根号外的因式就是这个二次根式的系数,如果系数是带分数,还要化成假分数;
(2)不是同类二次根式的不能合并,但是决不能丢弃,它们也是结果的一部分;
(3)在进行二次根式的加减运算时,整式加法的交换律、结合律及去括号、添括号法则仍然适用
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
分析(1)先化成最简二次根式,再加减;(2)把每一个二次根式化成最简二次根式,有括号的利用去括号法则去掉括号,然后进行加减运算;(3)先把二次根式进行化简,再把同类二次根式合并.
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
分析(1)先化成最简二次根式,再加减;(2)把每一个二次根式化成最简二次根式,有括号的利用去括号法则去掉括号,然后进行加减运算;(3)先把二次根式进行化简,再把同类二次根式合并.
解析 (1)原式= .
(2)原式=
.
(3)原式= .
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
分析(1)先化成最简二次根式,再加减;(2)把每一个二次根式化成最简二次根式,有括号的利用去括号法则去掉括号,然后进行加减运算;(3)先把二次根式进行化简,再把同类二次根式合并.
解析 (1)原式= .
(2)原式=
.
(3)原式= .
方法归纳
二次根式的加减运算的步骤:化简→判断→合并.
经典例题
题型一 同类二次根式概念的应用
例1 已知两个最简二次根式 与 是同类二次根式,求 .
题型一 同类二次根式概念的应用
例1 已知两个最简二次根式 与 是同类二次根式,求 .
解析 ∵两个最简二次根式 与 是同类二次根式,∴ ,解得 ,∴ .
题型一 同类二次根式概念的应用
例1 已知两个最简二次根式 与 是同类二次根式,求 .
解析 ∵两个最简二次根式 与 是同类二次根式,∴ ,解得 ,∴ .
点拨
解此类题目,要紧扣同类二次根式的定义,列出方程(组),从而解决问题.
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
分析 先化为最简二次根式,再根据二次根式的加减运算将同类二次根式进行合并.
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
分析 先化为最简二次根式,再根据二次根式的加减运算将同类二次根式进行合并.
解析 (1)原式= .
(2)原式= .
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
分析 先化为最简二次根式,再根据二次根式的加减运算将同类二次根式进行合并.
解析 (1)原式= .
(2)原式= .
点拨 进行二次根式的加减运算时应注意:
(1)被开方数若是带分数要化成假分数;
(2)运算的结果是一个二次根式与多项式的积时,需要将多项式加上括号.
易错易混
易错点 误判同类二次根式
例 下列二次根式中,与 是同类二次根式的是( )
A. B. C. D.
易错点 误判同类二次根式
例 下列二次根式中,与 是同类二次根式的是( )
A. B. C. D.
解析 =2 . =2 ,与 不是同类二次根式;
=2 ,与 不是同类二次根式;
=4 ,与 是同类二次根式;
=2 ,与 不是同类二次根式.故选 C.
答案 C
易错点 误判同类二次根式
例 下列二次根式中,与 是同类二次根式的是( )
A. B. C. D.
解析 =2 . =2 ,与 不是同类二次根式;
=2 ,与 不是同类二次根式;
=4 ,与 是同类二次根式;
=2 ,与 不是同类二次根式.故选 C.
答案 C
易错警示 本题容易出现的错误是不对二次根式进行化简,直接判断被开方数是否相等,从而确定是不是同类二次根式.
3 二次根式的加减
知识点一 同类二次根式
内容
举例
概念
特别提醒
知识点一 同类二次根式
内容
举例
概念
几个二次根式化成最简二次根式后,如果它们的被开方数相同,那么这几个二次根式是同类二次根式
如 与2 ,
与 等
特别提醒
(1)判断几个二次根式是不是同类二次根式,关键是把各个二次根式准确地化成最简二次根式,再观察它们的被开方数是否相同;
(2)在没有化成最简二次根式之前,无法判断两个二次根式是不是同类二次根式,因此,化成最简二次根式是判断同类二次根式的前提条件
例1 以下二次根式:① ;② ;③ ;④ .
与 是同类二次根式的是( )
A.①和② B.②和③ C.①和④ D.③和④
例1 以下二次根式:① ;② ;③ ;④ .
与 是同类二次根式的是( )
A.①和② B.②和③ C.①和④ D.③和④
解析 ∵ =2 , =2, = , =3 ,
∴与 是同类二次根式的是①和④.
答案 C
例1 以下二次根式:① ;② ;③ ;④ .
与 是同类二次根式的是( )
A.①和② B.②和③ C.①和④ D.③和④
解析 ∵ =2 , =2, = , =3 ,
∴与 是同类二次根式的是①和④.
答案 C
温馨提示 要判断几个二次根式是不是同类二次根式,不要被表面上的被开方数迷惑,要把它化成最简二次根式后再作出判断.
知识点二 二次根式的加减
名称
内容
步骤
二次根式的
加减
特别
提醒
知识点二 二次根式的加减
名称
内容
步骤
二次根式的
加减
一般地,二次根式相加减,先把各个二次根式分别化成最简二次根式,然后再将同类二次根式分别合并有括号时,要先去括号
(1)化成最简二次根式;
(2)找出同类二次根式;
(3)合并同类二次根式
特别
提醒
(1)在运算过程中要注意,根号外的因式就是这个二次根式的系数,如果系数是带分数,还要化成假分数;
(2)不是同类二次根式的不能合并,但是决不能丢弃,它们也是结果的一部分;
(3)在进行二次根式的加减运算时,整式加法的交换律、结合律及去括号、添括号法则仍然适用
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
分析(1)先化成最简二次根式,再加减;(2)把每一个二次根式化成最简二次根式,有括号的利用去括号法则去掉括号,然后进行加减运算;(3)先把二次根式进行化简,再把同类二次根式合并.
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
分析(1)先化成最简二次根式,再加减;(2)把每一个二次根式化成最简二次根式,有括号的利用去括号法则去掉括号,然后进行加减运算;(3)先把二次根式进行化简,再把同类二次根式合并.
解析 (1)原式= .
(2)原式=
.
(3)原式= .
例2 计算:(1) (2) ;
(3) (a≥0,b>0).
分析(1)先化成最简二次根式,再加减;(2)把每一个二次根式化成最简二次根式,有括号的利用去括号法则去掉括号,然后进行加减运算;(3)先把二次根式进行化简,再把同类二次根式合并.
解析 (1)原式= .
(2)原式=
.
(3)原式= .
方法归纳
二次根式的加减运算的步骤:化简→判断→合并.
经典例题
题型一 同类二次根式概念的应用
例1 已知两个最简二次根式 与 是同类二次根式,求 .
题型一 同类二次根式概念的应用
例1 已知两个最简二次根式 与 是同类二次根式,求 .
解析 ∵两个最简二次根式 与 是同类二次根式,∴ ,解得 ,∴ .
题型一 同类二次根式概念的应用
例1 已知两个最简二次根式 与 是同类二次根式,求 .
解析 ∵两个最简二次根式 与 是同类二次根式,∴ ,解得 ,∴ .
点拨
解此类题目,要紧扣同类二次根式的定义,列出方程(组),从而解决问题.
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
分析 先化为最简二次根式,再根据二次根式的加减运算将同类二次根式进行合并.
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
分析 先化为最简二次根式,再根据二次根式的加减运算将同类二次根式进行合并.
解析 (1)原式= .
(2)原式= .
题型二 二次根式的加减运算
例2 计算:(1) ;
(2) .
分析 先化为最简二次根式,再根据二次根式的加减运算将同类二次根式进行合并.
解析 (1)原式= .
(2)原式= .
点拨 进行二次根式的加减运算时应注意:
(1)被开方数若是带分数要化成假分数;
(2)运算的结果是一个二次根式与多项式的积时,需要将多项式加上括号.
易错易混
易错点 误判同类二次根式
例 下列二次根式中,与 是同类二次根式的是( )
A. B. C. D.
易错点 误判同类二次根式
例 下列二次根式中,与 是同类二次根式的是( )
A. B. C. D.
解析 =2 . =2 ,与 不是同类二次根式;
=2 ,与 不是同类二次根式;
=4 ,与 是同类二次根式;
=2 ,与 不是同类二次根式.故选 C.
答案 C
易错点 误判同类二次根式
例 下列二次根式中,与 是同类二次根式的是( )
A. B. C. D.
解析 =2 . =2 ,与 不是同类二次根式;
=2 ,与 不是同类二次根式;
=4 ,与 是同类二次根式;
=2 ,与 不是同类二次根式.故选 C.
答案 C
易错警示 本题容易出现的错误是不对二次根式进行化简,直接判断被开方数是否相等,从而确定是不是同类二次根式.
