7.3 实验(一):测定金属的电阻率(同时练习使用螺旋测微器)
文档属性
| 名称 | 7.3 实验(一):测定金属的电阻率(同时练习使用螺旋测微器) |  | |
| 格式 | rar | ||
| 文件大小 | 523.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-12-26 14:58:19 | ||
图片预览







文档简介
(共27张PPT)
学案3 实验(一):测定金属的电阻率
(同时练习使用螺旋测微器)
一、实验目的
1.掌握电流表、电压表和滑动变阻器的使用方法及电流表和电压表的读数方法。
2.掌握螺旋测微器及游标卡尺的原理及读数方法。
3.会用伏安法测电阻,进一步测定金属的电阻率。
1.螺旋测微器的构造原理及读数
二、实验原理
(1) 构造
如图所示是常用的螺旋测微器,它的小
砧A和固定刻度B固定在框架C上。旋钮D、
微调旋钮D′和可动刻度E、测微螺杆F连在
一起,通过精密螺纹套在B上。
(2) 原理
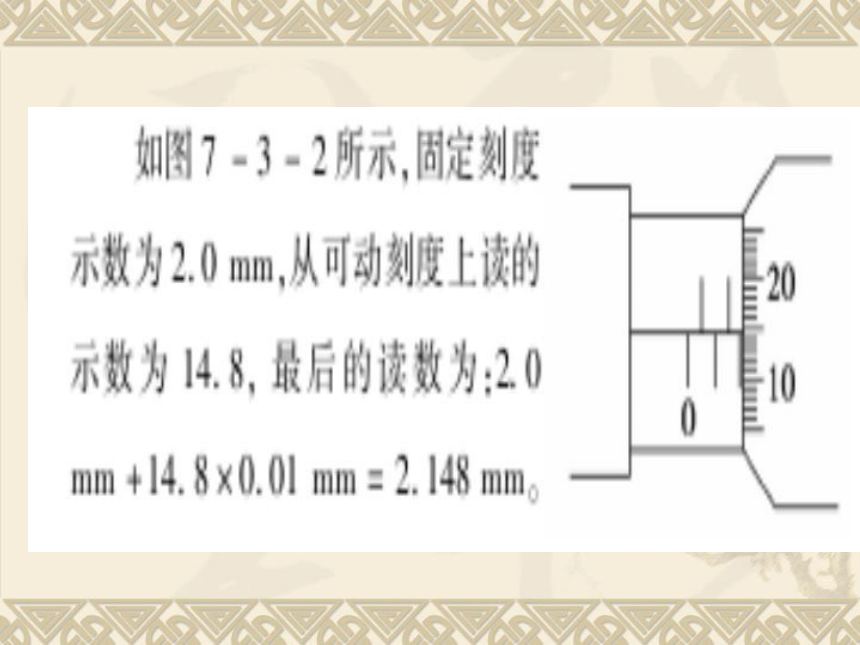
测微螺杆F与固定刻度B之间的精密螺纹的螺距为0.5 mm,即旋钮D每旋转一周,F前进或后退0.5 mm,而可动刻度E上的刻度为50等份,每转动一小格,F前进或后退0.01 mm。即螺旋测微器的精确度为0.01 mm。读数时误差出现在毫米的千分位上,因此,螺旋测微器又叫千分尺。
(3)读数:测量时被测物体长度的整数毫米数由固定刻度读出,小数部分由可动刻度读出。
测量值(毫米)=固定刻度数(毫米)(注意半毫米刻线是否露出)+可动刻度数(估读一位)×0.01(毫米)
2.游标卡尺(如图)
(1)构造:主尺、游标
尺(主尺和游标尺上各有一
个内外测量爪)、游标尺上
还有一个深度尺,尺身上还有一个紧固螺钉。
(2)用途:测量厚度、长度、深度、内径、外径。
(3)原理:利用主尺的最小分度与游标尺的最小分度的差值制成。
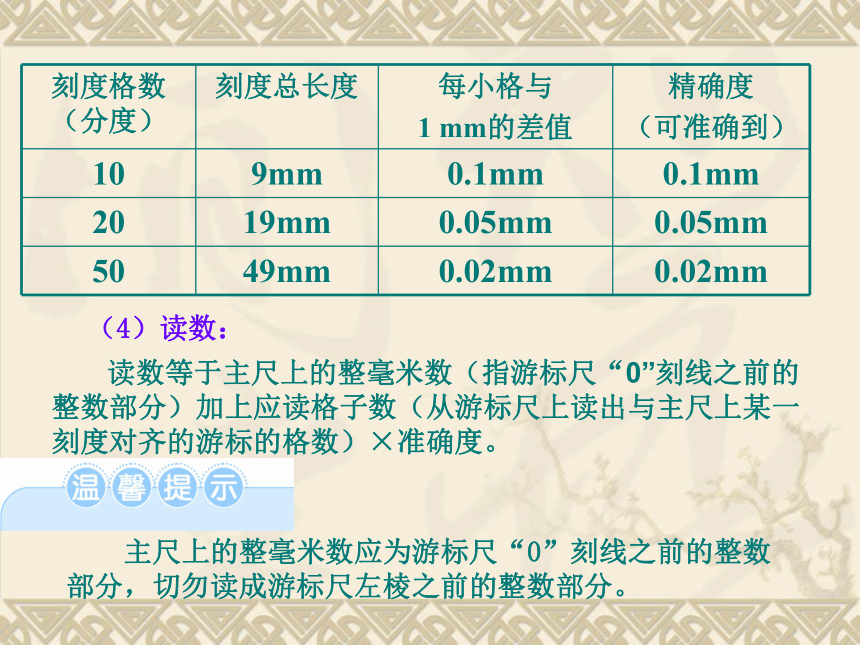
不管游标尺上有多少个小等分刻度,它的刻度部分的总长度比主尺上的同样多的小等分刻度少1 mm。常见的游标卡尺的游标尺上小等分刻度有10个的、20个的、50个的,见下表:
刻度格数(分度) 刻度总长度 每小格与
1 mm的差值 精确度
(可准确到)
10 9mm 0.1mm 0.1mm
20 19mm 0.05mm 0.05mm
50 49mm 0.02mm 0.02mm
(4)读数:
读数等于主尺上的整毫米数(指游标尺“0”刻线之前的整数部分)加上应读格子数(从游标尺上读出与主尺上某一刻度对齐的游标的格数)×准确度。
主尺上的整毫米数应为游标尺“0”刻线之前的整数部分,切勿读成游标尺左棱之前的整数部分。
3.伏安法测电阻
(1)电流表的内接法和外接法的比较
内接法 外接法
电路图
误差原因 电流表分压
U测=Ux+UA 电压表分流
I测=Ix+IV
电阻测量值 R测=U测/I测=
Rx+RA>Rx
测量值大于真实值 R测=U测/I测
=RxRV/(Rx+RV)测量值小于真实值
适用条件 RA<>Rx
适用于测量 大电阻 小电阻
②试触法
若不知Rx的大约阻值,可采用“试触法”,
将电路如图所示连接,空出电压表的一个接
头S,然后将S分别与a,b接触一下,
观察两表示数变化情况。
(2)两种电路的选择
①定量判定法
若已知待测电阻的大致阻值Rx,电流表的内阻RA和电压表的内阻RV,则:当Rx/RA>RV/Rx时,选用“内接法”,当Rx/RAa.若电流表示数变化明显,说明电压表分流作用较强,即
Rx阻值较大,应采用“内接法”,S应接b。
b.若电压表示数变化明显,说明电流表分压作用较强,即
Rx阻值较小,应采用“外接法”,S应接a。
4.电阻率的测定原理
把金属丝接入如图所示的电路中,用
电压表测金属丝两端的电压,用电流表测
金属丝中的电流,根据Rx=U/I计算金属丝
的电阻Rx,然后用米尺测量金属丝的有效
长度l,用螺旋测微器测量金属丝的直径d
,计算出金属丝的横截面积S;根据电阻定律Rx= l/S,得出计算金属丝电阻率的公式 =RxS/l= d2U/(4lI)。
四、实验步骤
三、实验器材
被测金属丝、米尺、螺旋测微器、电压表、电流表、直流电源、开关、滑动变阻器、导线若干。
3.按图所示的电路连接好器材,注意滑动
变阻器应调在阻值最大的位置,电流表和电压
表选择好适当的量程。
4.闭合开关S,调节滑动变阻器的滑动触片,
读出几组相应的电流表和电压表的示数I和U的值,记入记录表格内。
5.打开开关S,拆除电路,整理好实验器材。
2.用米尺测量接入电路中的被测金属丝的长度l,测量三次,将测量结果记入表格中。
1. 用螺旋测微器在金属丝的三个不同位置分别测量金属丝的直径,将测量结果记入表格,求直径的平均值,计算出金属丝的横截面积。
(1)金属丝的长度 =_____cm=______m;
(3)金属丝的电阻 =__________ 。
(4)金属丝材料的电阻率 = =_________ ·m。
(1)金属丝的长度 =_____cm=______m;
6.数据处理
根据上面记录的数据,完成以下表格内容:
实验次数 长度l/cm 长度平均 /cm 直径d/mm 直径平均 /mm 横截面积S/mm2
1
2
3
实验次数 电压U/V 电流I/A 电阻R/ /
1
2
3
(2)金属丝的横截面积S=________mm2=________m2。
实验次数 长度l/cm 长度平均 /cm 直径d/mm 直径平均 /mm 横截面积S/mm2
1
2
3
五、注意事项
1.为了减小金属丝横截面积带来的误差,测量直径时用螺旋测微器在金属丝的三个不同位置各测量一次,取平均值;
2.测量金属丝的长度应该在接入电路后且在拉直的状态下进行,为减小误差应测量三次取平均值;
3.为了减少由于温度变化而带来的测量误差,实验中注意通电时间不宜过长、电流不宜过大;
4.测量电路采用电流表外接法,调节滑动变阻器阻值时注意同时观察两个电表的示数,尽量使表的指针偏转较大,以减少读数误差,但是注意防止超过量程;
5.为了减小实验误差,测量金属丝的电阻时一般电流I、电压U测量多次,求出对应的电阻后取电阻的平均值,实验中也可以利用U-I图线求电阻;
6.闭合开关S之前,一定要使滑动变阻器的滑动片处在有效电阻最大的位置。
7.对螺旋测微器读数时,注意半毫米刻度线是否露出。
六、误差分析
1.金属丝的横截面积是利用直径计算而得到的,直径的测量是产生误差的主要来源之一;
2.采用伏安法测量金属丝的电阻时,必然带来系统误差;
3.金属丝的长度测量、电流表和电压表的读数等会带来偶然误差;
4.由于金属丝通电后发热升温,会使金属丝的电阻率变大,造成测量误差。
考点1 游标卡尺及螺旋测微器的读数
【例1】(1)在测定金属的电阻率实验中,用螺旋测微器测量金属丝的直径,示数如图甲所示,读数为 mm。
(2)在用单摆测定重力加速度实验中,用游标为20 分度的卡尺测量摆球的直径,示数如图所示,读数为 cm。
0.617
0.675
【解析】d1=0.5 mm+11.7×0.01 mm=0.617 mm
d2=6 mm+15×0.05 mm=0.675 cm
(1)把握好游标卡尺及螺旋测微器的读数方法。
(2)游标卡尺的读数没有估读,而螺旋测微器可动部分的读数应估读一位。
1
某同学用游标卡尺测量一圆柱体的长度l,用螺旋测微器测量该圆柱体的直径d,示数如图。由图可读出l= cm,d= mm。
2.25
6.860
【解析】本题考查了游标卡尺与螺旋
测微器的使用与读数。游标卡尺上有
10个等分格,精度为0.1 mm,游标
尺上第5根刻线与主尺整毫米刻线重
合,所以读数为0.5 mm,所以圆柱
体长度为22.5 mm=2.25 cm。固定
刻度的整毫米数为6 mm,且半毫米刻线已经露出,可动刻度已经转过36条刻线,所以圆柱体直径为6.860 mm。
【例2】某实验小组利用实验室提供的器材探究一种金属丝的电阻率,所用的器材包括:输出为3V的直流稳压电源、电流表、待测金属丝、米尺、电阻箱、开关和导线等(如图1)。
(1)他们截取了一段金属丝,拉直后固定在
绝缘的米尺上,并在金属丝上夹上一个小金属
夹,金属夹可在金属丝上移动。请根据现有器
材,设计实验电路,并连接电路实物图(如图)。
(2)实验的主要步骤如下:
①正确连接电路,设定电阻箱的阻值,
开启电源,合上开关;
②读出电流表的示数,记录金属夹的位置;
③断开开关,________________。合上开关
,重复②的操作。
考点2 测定金属电阻率的原理
(3)该小组测得电流与金属丝接入长度关系的数据,并据此给出了如图2中的关系图线,其斜率为_______A-1·m-1 (保留三位有效数字);图线纵轴截距与电源电动势的乘积代表了______的电阻之和。
(4)他们使用螺旋测微器测量金属丝的直径,示数如图3所示。金属丝的直径是___________。如图2中线的斜率、电源电动势和金属丝横截面积的乘积代表的物理量是_____________,其数值和单位为___________(保留三位有效数字)。
【答案】(1)如图甲、乙
(2)③读出接入电路中的金属丝的长度
(3)1.63 电源的内阻与电阻箱
(4)0.200mm 金属丝的电阻率
1.54×10-7 Ω·m
【解析】本题以创新型实验的形式考查了电阻率的测量,解答时首先要看明白实验的原理,对利用图象获取信息的能力有较高的要求。
依据实验器材和实验目的测量金属丝的电阻率,电路图如图甲所示;电路实物图如图乙所示,依据闭合电路欧姆定律得E=I(r+R0+Rx),参照题目给出的图象可得/I=(r+R0)/E= /(ES)·L,可见直线的斜率k= /(ES),可知斜率、电源电动势和金属丝横截面积的乘积代表的物理量是金属丝的电阻率 ,其数值和单位为1.54×10-7 Ω·m;依据直线可得其斜率为1.63 A-1·m-1,截距为(r+R0)/E,则图线纵轴截距与电源电动势的乘积为(r+R0) 。金属丝的直径是0.200mm。
实物连图时,要注意以下几点:
(1)接线要接到接线柱上,并且切勿交叉。
(2)要让电流从电压表或电流表的“+”极流入,“-”极流出,同时要注意正确连接电表的量程。
某同学想要了解导线在质量相同时,电阻与截面积的关系,选取了材料相同、质量相等的5卷导线,进行了如下实验:
(1)用螺旋测微器测量某一导线的直径如图所示。读得直径d=______mm。
(2)该同学经实验测量及相关计算得到如下数据。
请你根据以上数据判断,该种导线的电阻R与截面积S是否满足反比关系?若满足反比关系请说明理由;若不满足,请写出R与S应满足的关系。 不满足,R与S2成反比(或RS2=常量)
(3)若导线的电阻率 =5.1×10-7 ·m,则表中阻值为3.1 的导线长度l=_____m(结果保留两位有效数字)。
电阻R( ) 121.0 50.0 23.9 10.0 3.1
导线直径d(mm) 0.801 0.999 1.201 1.494 1.998
导线截面积S(mm2) 0.504 0.784 1.331 1.753 3.135
19
2
1.200
【解析】(1)固定刻度读数为1 mm,可动刻度读数为0.200 mm,所以读数为1.200 mm。(2)由表中数据,分析发现RS2=常量,所以R与S不满足反比关系。(3)根据电阻公式R=ρl/S得l=RS/ρ,代入数据得l≈19 m。
【例3】某研究性学习小组设计了如图所示的电路,用来研究稀盐水溶液的电阻率与浓度的关系。图中E为直流电源,K为开关,K1为单刀双掷开关,V为电压表,A为多量程电流表,R为滑 动变阻器,Rx为待测稀盐水溶液液柱。
(1)实验时,闭合K之前将R的滑片P置于____(填“C”或“D”) 端;当用电流表外接法测量Rx的阻值时,K1应置于位置___(填“1”或“2”)。
考点3 实验拓展创新
D
1
(2)在一定条件下,用电流表内、外接法得到Rx的电阻率随浓度变化的两条曲线如图所示(不计由于通电导致的化学变化),实验中Rx的通电面积为20 cm2,长度为20 cm,用内接法测量Rx的阻值是3 500 Ω,则其电阻率为 _____ ·m,由图中对应曲线_____(填“1”或 “2”)可得此时溶液浓度约为_____________ %(结果保留两位有效数字)。
【解析】(1)滑动变阻器是分压作用,为保护仪表,开始滑片P置于D端,电流表外接法测Rx阻值时,K1应置于1位置。
(2)由Rx= l/S得, =RxS/l=(3500×20×10-4)/(20×10-2) ·m=35 ·m。
因为Rx=3 500 ,这一阻值远大于电流表内阻,而与电压表内阻较接近,所以选用电流表内接法误差较小,测量较准确,曲线1对应的较准确,所以曲线1对应内接法。由曲线1可得此时溶液浓度约为0.012%。
35
0.011~0.014间的数据
1
有一根圆台状匀质合金棒如图1所示,某同学猜测其电阻的大小与该合金棒的电阻率 、长度L和两底面直径d、D有关。他进行了如下实验:
(1) 用游标卡尺测量合金棒的两底面直径d、D和长度L。图2中游标卡尺(游标尺上有20个等分刻度)的读数L=_______cm。
(2)测量该合金棒电阻的实物电路如图3所示(相关器材的参数已在图中标出)。该合金棒的电阻约为几个欧姆。图中有一处连接不当的导线是______。(用标注在导线旁的数字表示)
⑥
3
图
1
图3
图
2
9.940
(3)改正电路后,通过实验测得合金棒的电阻R=6.72 。根据电阻定律计算电阻率为 、长为L、直径分别为d和D的圆柱状合金棒的电阻分别为Rd= 13.3 、RD=3.38 。他发现:在误差允许范围内,电阻R满足R2=Rd·RD,由此推断该圆台状合金棒的电阻R=____________。(用 、L、d、D表示)
4 L/( dD)
【解析】(1)主尺读数9.9 cm,游标尺读数0.05 mm×8=0.40 mm,两者相加即得读数为99.40 mm,即9.940 cm。
(2)由于合金棒的电阻远小于电压表内阻,电流表应采用外接法,连接不当的导线是⑥。
(3) 。
1.甲同学用游标尺测量一物体的长度 ,用螺旋测微器测量该物体的直径d,示数如图所示。由图可得 =_____mm;d=_____mm。
【答案】100.4 6.520
【解析】 =100 mm+4×0.1 mm=100.4 mm
d=6.5 mm+2.0×0.01 mm=6.520 mm。
100.4
6.520
2.一个未知电阻,无法估计其电阻值,某同学用伏安法测量此电阻,用图(a)(b)两种电路各测一次,用 (a)图所测数据为3.0 V、3.0 mA,用 (b)图测得的数据是2.9 V、4.0 mA,由此可知,用_______图测得Rx的误差较小,测量值Rx=_____。
【答案】(a) 1000 Ω
ΔU=0.1 V
ΔI=1 mA
ΔU/U1=3%
ΔI/I1=33%
结论:电流变化相对明显,应采用内接法。R=U/I=3.0/3.0 Ω=1 000 Ω。
【解析】绝对变化
相对变化
(a)
1000 Ω
3.在用伏安法测电阻的实验中,所用电压表的内阻约为20 kΩ,电流表的内阻约为10 Ω,选择能够尽量减小误差的电路图接线进行实验,读得的各组数据用实心圆点标于坐标图上,如图所示。
(1)根据各点表示的数据描出I-U图线,由
此求得该电阻的阻值Rx=——Ω(保留两位有效数字)。
(2)画出“伏安法”测量该电阻的电路图。
【答案】见解析
【解析】(1)图线如图(1)所示
Rx=ΔU/ΔI=2.4×103 Ω (2.3×103 Ω~2.5×103 Ω)。
(2)因满足 ,故采用电流表内接法,故电路如图(2)所示。
学案3 实验(一):测定金属的电阻率
(同时练习使用螺旋测微器)
一、实验目的
1.掌握电流表、电压表和滑动变阻器的使用方法及电流表和电压表的读数方法。
2.掌握螺旋测微器及游标卡尺的原理及读数方法。
3.会用伏安法测电阻,进一步测定金属的电阻率。
1.螺旋测微器的构造原理及读数
二、实验原理
(1) 构造
如图所示是常用的螺旋测微器,它的小
砧A和固定刻度B固定在框架C上。旋钮D、
微调旋钮D′和可动刻度E、测微螺杆F连在
一起,通过精密螺纹套在B上。
(2) 原理
测微螺杆F与固定刻度B之间的精密螺纹的螺距为0.5 mm,即旋钮D每旋转一周,F前进或后退0.5 mm,而可动刻度E上的刻度为50等份,每转动一小格,F前进或后退0.01 mm。即螺旋测微器的精确度为0.01 mm。读数时误差出现在毫米的千分位上,因此,螺旋测微器又叫千分尺。
(3)读数:测量时被测物体长度的整数毫米数由固定刻度读出,小数部分由可动刻度读出。
测量值(毫米)=固定刻度数(毫米)(注意半毫米刻线是否露出)+可动刻度数(估读一位)×0.01(毫米)
2.游标卡尺(如图)
(1)构造:主尺、游标
尺(主尺和游标尺上各有一
个内外测量爪)、游标尺上
还有一个深度尺,尺身上还有一个紧固螺钉。
(2)用途:测量厚度、长度、深度、内径、外径。
(3)原理:利用主尺的最小分度与游标尺的最小分度的差值制成。
不管游标尺上有多少个小等分刻度,它的刻度部分的总长度比主尺上的同样多的小等分刻度少1 mm。常见的游标卡尺的游标尺上小等分刻度有10个的、20个的、50个的,见下表:
刻度格数(分度) 刻度总长度 每小格与
1 mm的差值 精确度
(可准确到)
10 9mm 0.1mm 0.1mm
20 19mm 0.05mm 0.05mm
50 49mm 0.02mm 0.02mm
(4)读数:
读数等于主尺上的整毫米数(指游标尺“0”刻线之前的整数部分)加上应读格子数(从游标尺上读出与主尺上某一刻度对齐的游标的格数)×准确度。
主尺上的整毫米数应为游标尺“0”刻线之前的整数部分,切勿读成游标尺左棱之前的整数部分。
3.伏安法测电阻
(1)电流表的内接法和外接法的比较
内接法 外接法
电路图
误差原因 电流表分压
U测=Ux+UA 电压表分流
I测=Ix+IV
电阻测量值 R测=U测/I测=
Rx+RA>Rx
测量值大于真实值 R测=U测/I测
=RxRV/(Rx+RV)
适用条件 RA<
适用于测量 大电阻 小电阻
②试触法
若不知Rx的大约阻值,可采用“试触法”,
将电路如图所示连接,空出电压表的一个接
头S,然后将S分别与a,b接触一下,
观察两表示数变化情况。
(2)两种电路的选择
①定量判定法
若已知待测电阻的大致阻值Rx,电流表的内阻RA和电压表的内阻RV,则:当Rx/RA>RV/Rx时,选用“内接法”,当Rx/RA
Rx阻值较大,应采用“内接法”,S应接b。
b.若电压表示数变化明显,说明电流表分压作用较强,即
Rx阻值较小,应采用“外接法”,S应接a。
4.电阻率的测定原理
把金属丝接入如图所示的电路中,用
电压表测金属丝两端的电压,用电流表测
金属丝中的电流,根据Rx=U/I计算金属丝
的电阻Rx,然后用米尺测量金属丝的有效
长度l,用螺旋测微器测量金属丝的直径d
,计算出金属丝的横截面积S;根据电阻定律Rx= l/S,得出计算金属丝电阻率的公式 =RxS/l= d2U/(4lI)。
四、实验步骤
三、实验器材
被测金属丝、米尺、螺旋测微器、电压表、电流表、直流电源、开关、滑动变阻器、导线若干。
3.按图所示的电路连接好器材,注意滑动
变阻器应调在阻值最大的位置,电流表和电压
表选择好适当的量程。
4.闭合开关S,调节滑动变阻器的滑动触片,
读出几组相应的电流表和电压表的示数I和U的值,记入记录表格内。
5.打开开关S,拆除电路,整理好实验器材。
2.用米尺测量接入电路中的被测金属丝的长度l,测量三次,将测量结果记入表格中。
1. 用螺旋测微器在金属丝的三个不同位置分别测量金属丝的直径,将测量结果记入表格,求直径的平均值,计算出金属丝的横截面积。
(1)金属丝的长度 =_____cm=______m;
(3)金属丝的电阻 =__________ 。
(4)金属丝材料的电阻率 = =_________ ·m。
(1)金属丝的长度 =_____cm=______m;
6.数据处理
根据上面记录的数据,完成以下表格内容:
实验次数 长度l/cm 长度平均 /cm 直径d/mm 直径平均 /mm 横截面积S/mm2
1
2
3
实验次数 电压U/V 电流I/A 电阻R/ /
1
2
3
(2)金属丝的横截面积S=________mm2=________m2。
实验次数 长度l/cm 长度平均 /cm 直径d/mm 直径平均 /mm 横截面积S/mm2
1
2
3
五、注意事项
1.为了减小金属丝横截面积带来的误差,测量直径时用螺旋测微器在金属丝的三个不同位置各测量一次,取平均值;
2.测量金属丝的长度应该在接入电路后且在拉直的状态下进行,为减小误差应测量三次取平均值;
3.为了减少由于温度变化而带来的测量误差,实验中注意通电时间不宜过长、电流不宜过大;
4.测量电路采用电流表外接法,调节滑动变阻器阻值时注意同时观察两个电表的示数,尽量使表的指针偏转较大,以减少读数误差,但是注意防止超过量程;
5.为了减小实验误差,测量金属丝的电阻时一般电流I、电压U测量多次,求出对应的电阻后取电阻的平均值,实验中也可以利用U-I图线求电阻;
6.闭合开关S之前,一定要使滑动变阻器的滑动片处在有效电阻最大的位置。
7.对螺旋测微器读数时,注意半毫米刻度线是否露出。
六、误差分析
1.金属丝的横截面积是利用直径计算而得到的,直径的测量是产生误差的主要来源之一;
2.采用伏安法测量金属丝的电阻时,必然带来系统误差;
3.金属丝的长度测量、电流表和电压表的读数等会带来偶然误差;
4.由于金属丝通电后发热升温,会使金属丝的电阻率变大,造成测量误差。
考点1 游标卡尺及螺旋测微器的读数
【例1】(1)在测定金属的电阻率实验中,用螺旋测微器测量金属丝的直径,示数如图甲所示,读数为 mm。
(2)在用单摆测定重力加速度实验中,用游标为20 分度的卡尺测量摆球的直径,示数如图所示,读数为 cm。
0.617
0.675
【解析】d1=0.5 mm+11.7×0.01 mm=0.617 mm
d2=6 mm+15×0.05 mm=0.675 cm
(1)把握好游标卡尺及螺旋测微器的读数方法。
(2)游标卡尺的读数没有估读,而螺旋测微器可动部分的读数应估读一位。
1
某同学用游标卡尺测量一圆柱体的长度l,用螺旋测微器测量该圆柱体的直径d,示数如图。由图可读出l= cm,d= mm。
2.25
6.860
【解析】本题考查了游标卡尺与螺旋
测微器的使用与读数。游标卡尺上有
10个等分格,精度为0.1 mm,游标
尺上第5根刻线与主尺整毫米刻线重
合,所以读数为0.5 mm,所以圆柱
体长度为22.5 mm=2.25 cm。固定
刻度的整毫米数为6 mm,且半毫米刻线已经露出,可动刻度已经转过36条刻线,所以圆柱体直径为6.860 mm。
【例2】某实验小组利用实验室提供的器材探究一种金属丝的电阻率,所用的器材包括:输出为3V的直流稳压电源、电流表、待测金属丝、米尺、电阻箱、开关和导线等(如图1)。
(1)他们截取了一段金属丝,拉直后固定在
绝缘的米尺上,并在金属丝上夹上一个小金属
夹,金属夹可在金属丝上移动。请根据现有器
材,设计实验电路,并连接电路实物图(如图)。
(2)实验的主要步骤如下:
①正确连接电路,设定电阻箱的阻值,
开启电源,合上开关;
②读出电流表的示数,记录金属夹的位置;
③断开开关,________________。合上开关
,重复②的操作。
考点2 测定金属电阻率的原理
(3)该小组测得电流与金属丝接入长度关系的数据,并据此给出了如图2中的关系图线,其斜率为_______A-1·m-1 (保留三位有效数字);图线纵轴截距与电源电动势的乘积代表了______的电阻之和。
(4)他们使用螺旋测微器测量金属丝的直径,示数如图3所示。金属丝的直径是___________。如图2中线的斜率、电源电动势和金属丝横截面积的乘积代表的物理量是_____________,其数值和单位为___________(保留三位有效数字)。
【答案】(1)如图甲、乙
(2)③读出接入电路中的金属丝的长度
(3)1.63 电源的内阻与电阻箱
(4)0.200mm 金属丝的电阻率
1.54×10-7 Ω·m
【解析】本题以创新型实验的形式考查了电阻率的测量,解答时首先要看明白实验的原理,对利用图象获取信息的能力有较高的要求。
依据实验器材和实验目的测量金属丝的电阻率,电路图如图甲所示;电路实物图如图乙所示,依据闭合电路欧姆定律得E=I(r+R0+Rx),参照题目给出的图象可得/I=(r+R0)/E= /(ES)·L,可见直线的斜率k= /(ES),可知斜率、电源电动势和金属丝横截面积的乘积代表的物理量是金属丝的电阻率 ,其数值和单位为1.54×10-7 Ω·m;依据直线可得其斜率为1.63 A-1·m-1,截距为(r+R0)/E,则图线纵轴截距与电源电动势的乘积为(r+R0) 。金属丝的直径是0.200mm。
实物连图时,要注意以下几点:
(1)接线要接到接线柱上,并且切勿交叉。
(2)要让电流从电压表或电流表的“+”极流入,“-”极流出,同时要注意正确连接电表的量程。
某同学想要了解导线在质量相同时,电阻与截面积的关系,选取了材料相同、质量相等的5卷导线,进行了如下实验:
(1)用螺旋测微器测量某一导线的直径如图所示。读得直径d=______mm。
(2)该同学经实验测量及相关计算得到如下数据。
请你根据以上数据判断,该种导线的电阻R与截面积S是否满足反比关系?若满足反比关系请说明理由;若不满足,请写出R与S应满足的关系。 不满足,R与S2成反比(或RS2=常量)
(3)若导线的电阻率 =5.1×10-7 ·m,则表中阻值为3.1 的导线长度l=_____m(结果保留两位有效数字)。
电阻R( ) 121.0 50.0 23.9 10.0 3.1
导线直径d(mm) 0.801 0.999 1.201 1.494 1.998
导线截面积S(mm2) 0.504 0.784 1.331 1.753 3.135
19
2
1.200
【解析】(1)固定刻度读数为1 mm,可动刻度读数为0.200 mm,所以读数为1.200 mm。(2)由表中数据,分析发现RS2=常量,所以R与S不满足反比关系。(3)根据电阻公式R=ρl/S得l=RS/ρ,代入数据得l≈19 m。
【例3】某研究性学习小组设计了如图所示的电路,用来研究稀盐水溶液的电阻率与浓度的关系。图中E为直流电源,K为开关,K1为单刀双掷开关,V为电压表,A为多量程电流表,R为滑 动变阻器,Rx为待测稀盐水溶液液柱。
(1)实验时,闭合K之前将R的滑片P置于____(填“C”或“D”) 端;当用电流表外接法测量Rx的阻值时,K1应置于位置___(填“1”或“2”)。
考点3 实验拓展创新
D
1
(2)在一定条件下,用电流表内、外接法得到Rx的电阻率随浓度变化的两条曲线如图所示(不计由于通电导致的化学变化),实验中Rx的通电面积为20 cm2,长度为20 cm,用内接法测量Rx的阻值是3 500 Ω,则其电阻率为 _____ ·m,由图中对应曲线_____(填“1”或 “2”)可得此时溶液浓度约为_____________ %(结果保留两位有效数字)。
【解析】(1)滑动变阻器是分压作用,为保护仪表,开始滑片P置于D端,电流表外接法测Rx阻值时,K1应置于1位置。
(2)由Rx= l/S得, =RxS/l=(3500×20×10-4)/(20×10-2) ·m=35 ·m。
因为Rx=3 500 ,这一阻值远大于电流表内阻,而与电压表内阻较接近,所以选用电流表内接法误差较小,测量较准确,曲线1对应的较准确,所以曲线1对应内接法。由曲线1可得此时溶液浓度约为0.012%。
35
0.011~0.014间的数据
1
有一根圆台状匀质合金棒如图1所示,某同学猜测其电阻的大小与该合金棒的电阻率 、长度L和两底面直径d、D有关。他进行了如下实验:
(1) 用游标卡尺测量合金棒的两底面直径d、D和长度L。图2中游标卡尺(游标尺上有20个等分刻度)的读数L=_______cm。
(2)测量该合金棒电阻的实物电路如图3所示(相关器材的参数已在图中标出)。该合金棒的电阻约为几个欧姆。图中有一处连接不当的导线是______。(用标注在导线旁的数字表示)
⑥
3
图
1
图3
图
2
9.940
(3)改正电路后,通过实验测得合金棒的电阻R=6.72 。根据电阻定律计算电阻率为 、长为L、直径分别为d和D的圆柱状合金棒的电阻分别为Rd= 13.3 、RD=3.38 。他发现:在误差允许范围内,电阻R满足R2=Rd·RD,由此推断该圆台状合金棒的电阻R=____________。(用 、L、d、D表示)
4 L/( dD)
【解析】(1)主尺读数9.9 cm,游标尺读数0.05 mm×8=0.40 mm,两者相加即得读数为99.40 mm,即9.940 cm。
(2)由于合金棒的电阻远小于电压表内阻,电流表应采用外接法,连接不当的导线是⑥。
(3) 。
1.甲同学用游标尺测量一物体的长度 ,用螺旋测微器测量该物体的直径d,示数如图所示。由图可得 =_____mm;d=_____mm。
【答案】100.4 6.520
【解析】 =100 mm+4×0.1 mm=100.4 mm
d=6.5 mm+2.0×0.01 mm=6.520 mm。
100.4
6.520
2.一个未知电阻,无法估计其电阻值,某同学用伏安法测量此电阻,用图(a)(b)两种电路各测一次,用 (a)图所测数据为3.0 V、3.0 mA,用 (b)图测得的数据是2.9 V、4.0 mA,由此可知,用_______图测得Rx的误差较小,测量值Rx=_____。
【答案】(a) 1000 Ω
ΔU=0.1 V
ΔI=1 mA
ΔU/U1=3%
ΔI/I1=33%
结论:电流变化相对明显,应采用内接法。R=U/I=3.0/3.0 Ω=1 000 Ω。
【解析】绝对变化
相对变化
(a)
1000 Ω
3.在用伏安法测电阻的实验中,所用电压表的内阻约为20 kΩ,电流表的内阻约为10 Ω,选择能够尽量减小误差的电路图接线进行实验,读得的各组数据用实心圆点标于坐标图上,如图所示。
(1)根据各点表示的数据描出I-U图线,由
此求得该电阻的阻值Rx=——Ω(保留两位有效数字)。
(2)画出“伏安法”测量该电阻的电路图。
【答案】见解析
【解析】(1)图线如图(1)所示
Rx=ΔU/ΔI=2.4×103 Ω (2.3×103 Ω~2.5×103 Ω)。
(2)因满足 ,故采用电流表内接法,故电路如图(2)所示。
