2020-2021学年北师大版八年级数学下册1.3线段的垂直平分线培优训练(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册1.3线段的垂直平分线培优训练(Word版,附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 395.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览


文档简介
北师大版八年级下册数学第一章 三角形的证明
第3节《线段的垂直平分线》同步培优训练
选择。
1.如果三角形二条边的中垂线的交点在第三条边上,那么,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
2.如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取OC=OA,以A为圆心,AC长为半径画弧交AB于点P,则线段AP与AB的比是( )
A.∶2 B.1∶ C.∶ D.1∶
3.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2,则AE的长为( )
A. B.1 C. D.2
4.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,交AB于点E,AD平分∠BAC,则下列结论不正确的是( )
A.∠B的度数等于30° B.AC=AE=BE=AD
C.∠ADB的度数等于120° D.Rt△ADE≌Rt△BDE≌Rt△ADC
5.如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径画弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A.90° B.95° C.100° D.105°
6.如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段,分别以为圆心,以长为半径作弧,两弧的交点为;
(2)以为圆心,仍以长为半径作弧交的延长线于点;
(3)连接
下列说法不正确的是( )
A. B.
C.点是的外心 D.
7.如图,已知是的角平分线,是的垂直平分线,,,则的长为( )
A.6 B.5 C.4 D.
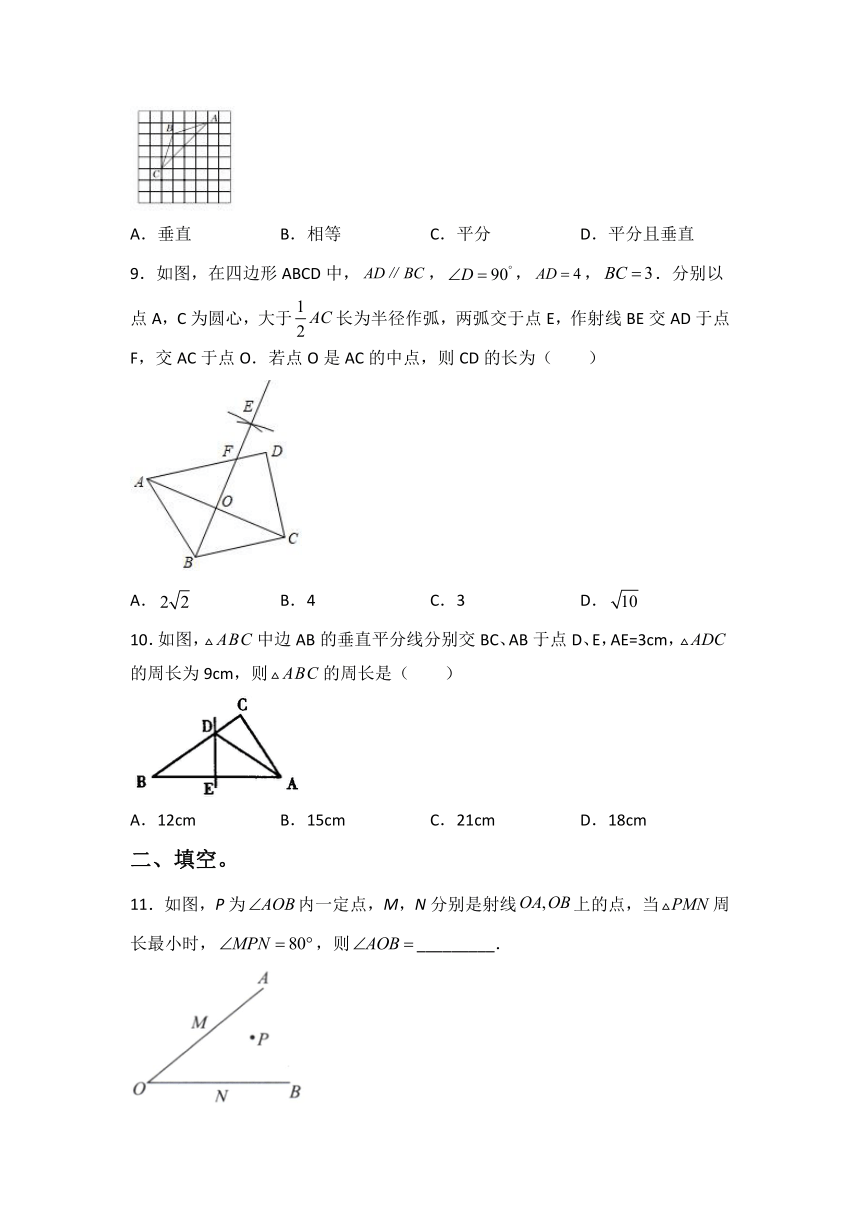
8.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A.垂直 B.相等 C.平分 D.平分且垂直
9.如图,在四边形ABCD中,,,,.分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )
A. B.4 C.3 D.
10.如图,中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,的周长为9cm,则的周长是( )
A.12cm B.15cm C.21cm D.18cm
填空。
11.如图,P为内一定点,M,N分别是射线上的点,当周长最小时,,则_________.
12.如图,△ABC中,∠A=100°,∠B=20°,边BC的垂直平分线分别交AB、BC于点E、D,则∠ACE的度数等于________.
13.如图,中,,是上一点,连接,将沿翻折,点落在边的点处,连接.若,,则长_____.
14.如图,△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD:∠CAD=4:1,则∠B=_______.
15.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为______.
解答。
16.如图,在四边形ABCD中,,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
17.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
18.如图,已知∠AOB和边OB上一点E,求作:一点P,使P到∠AOB两边的距离相等,且OP=EP.
19.如图,等边三角形中,的平分线交于点I,的垂直平分线分别交于点E,F.求证:.
20.如图,在中,边的垂直平分线交直线于点,垂足为点,边的垂直平分线交直线于点,垂足为点.
(1)当时,________;
(2)当为钝角时,猜想与的关系,并证明你的猜想.
答案
1-5:ADBBD 6-10:DDDAB
11.50°
12.40°
13.
14.40°
15.6
略
17.(1)5;(2)4
18.略
19.证明:连接.
∵垂直平分,
∴,同理.
又∵是等边三角形,
∴,
而分别平分,
∴.
∵,
∴,
同理,
∴为等边三角形.
∴,
∴.
20.(1)20;(2),证明略
第3节《线段的垂直平分线》同步培优训练
选择。
1.如果三角形二条边的中垂线的交点在第三条边上,那么,这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
2.如图,画线段AB的垂直平分线交AB于点O,在这条垂直平分线上截取OC=OA,以A为圆心,AC长为半径画弧交AB于点P,则线段AP与AB的比是( )
A.∶2 B.1∶ C.∶ D.1∶
3.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB,若BE=2,则AE的长为( )
A. B.1 C. D.2
4.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交BC于点D,交AB于点E,AD平分∠BAC,则下列结论不正确的是( )
A.∠B的度数等于30° B.AC=AE=BE=AD
C.∠ADB的度数等于120° D.Rt△ADE≌Rt△BDE≌Rt△ADC
5.如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径画弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A.90° B.95° C.100° D.105°
6.如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段,分别以为圆心,以长为半径作弧,两弧的交点为;
(2)以为圆心,仍以长为半径作弧交的延长线于点;
(3)连接
下列说法不正确的是( )
A. B.
C.点是的外心 D.
7.如图,已知是的角平分线,是的垂直平分线,,,则的长为( )
A.6 B.5 C.4 D.
8.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A.垂直 B.相等 C.平分 D.平分且垂直
9.如图,在四边形ABCD中,,,,.分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )
A. B.4 C.3 D.
10.如图,中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,的周长为9cm,则的周长是( )
A.12cm B.15cm C.21cm D.18cm
填空。
11.如图,P为内一定点,M,N分别是射线上的点,当周长最小时,,则_________.
12.如图,△ABC中,∠A=100°,∠B=20°,边BC的垂直平分线分别交AB、BC于点E、D,则∠ACE的度数等于________.
13.如图,中,,是上一点,连接,将沿翻折,点落在边的点处,连接.若,,则长_____.
14.如图,△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD:∠CAD=4:1,则∠B=_______.
15.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为______.
解答。
16.如图,在四边形ABCD中,,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
17.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
18.如图,已知∠AOB和边OB上一点E,求作:一点P,使P到∠AOB两边的距离相等,且OP=EP.
19.如图,等边三角形中,的平分线交于点I,的垂直平分线分别交于点E,F.求证:.
20.如图,在中,边的垂直平分线交直线于点,垂足为点,边的垂直平分线交直线于点,垂足为点.
(1)当时,________;
(2)当为钝角时,猜想与的关系,并证明你的猜想.
答案
1-5:ADBBD 6-10:DDDAB
11.50°
12.40°
13.
14.40°
15.6
略
17.(1)5;(2)4
18.略
19.证明:连接.
∵垂直平分,
∴,同理.
又∵是等边三角形,
∴,
而分别平分,
∴.
∵,
∴,
同理,
∴为等边三角形.
∴,
∴.
20.(1)20;(2),证明略
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
