2020-2021学年苏科版七年级下册课时练:第七章《 平面的图形认识(二)》(一)(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册课时练:第七章《 平面的图形认识(二)》(一)(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 186.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 00:00:00 | ||
图片预览


文档简介
2020-2021学年苏科版七年级下册课时练:第七章
《
平面的图形认识(二)》(一)
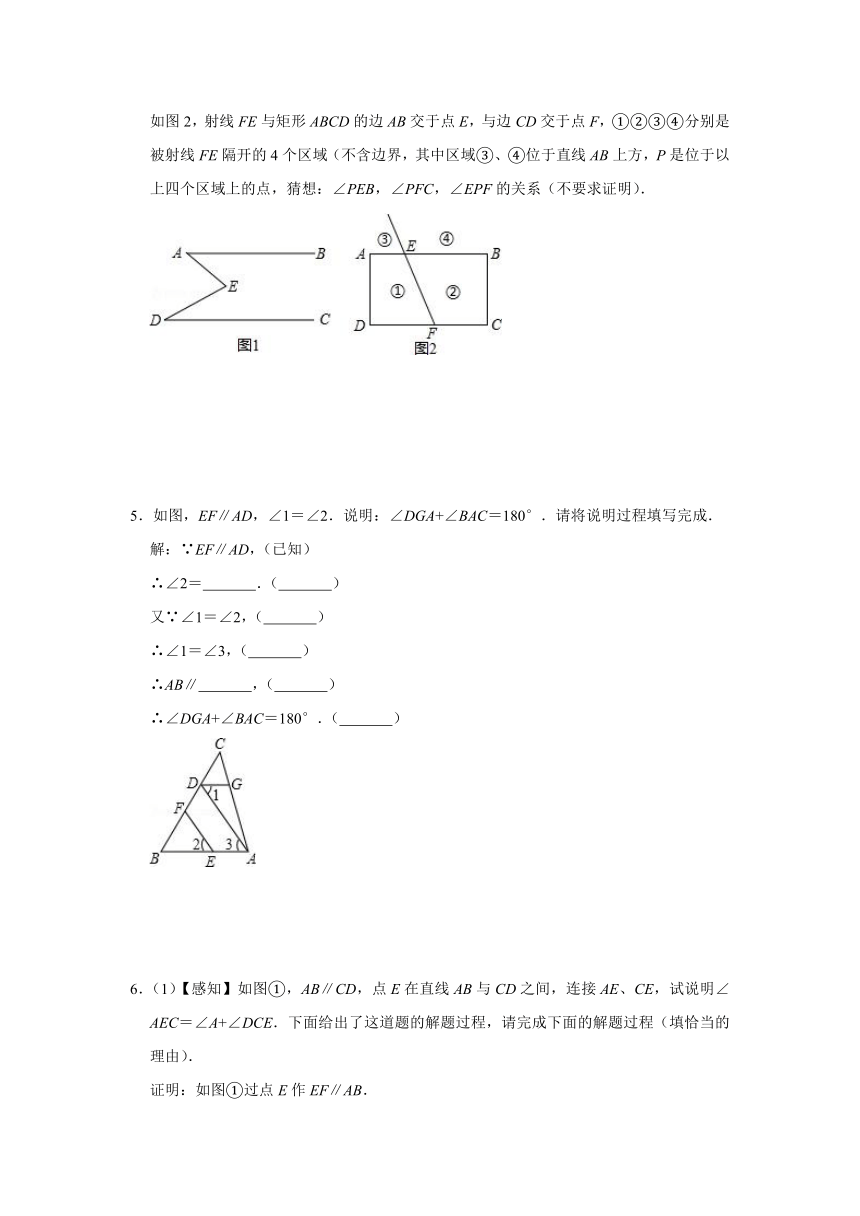
1.已知,如图①,点D,E,F,G是△ABC三边上的点,且FG∥AC,
(1)若∠EDC=∠FGC,试判断DE与BC是否平行,并说明理由.
(2)如图②,点M、N分别在边AC、BC上,且MN∥AB,连结GM,若∠A=60°,∠C=55°,∠FGM=4∠MGC,求∠GMN的度数.
(3)点M、N分别在射线AC、BC上,且MN∥AB,连结GM.若∠A=α,∠ACB=β,∠FGM=n∠MGC,直接写出∠GMN的度数(用含α,β,n的代数式表示)
2.已知:∠1=∠2,EG平分∠AEC.
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.试判断EF与CD的位置关系,并说明理由.
(2)如图②,∠MAE=140°,∠FEG=30°,当AB∥CD时,求∠NCE的度数;
(3)如图②,试写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
3.完成下面的证明:如图AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.求证:∠EGF=90°.
证明:∵HG∥AB,(已知)
∴∠1=∠3. (
)
∵HG∥CD(已知)
∴∠2=∠4. (
)
∵AB∥CD(已知)
∴∠BEF+∠EFD=180°(
)
∵EG平分∠BEF(已知)
∴∠1=∠BEF(
)
∵FG平分∠EFD(已知)
∴∠2=∠EFD(
)
∴∠1+∠2=?(
+
).
∴∠1+∠2=90°.
∴∠3+∠4=90°(
).
即∠EGF=90°.
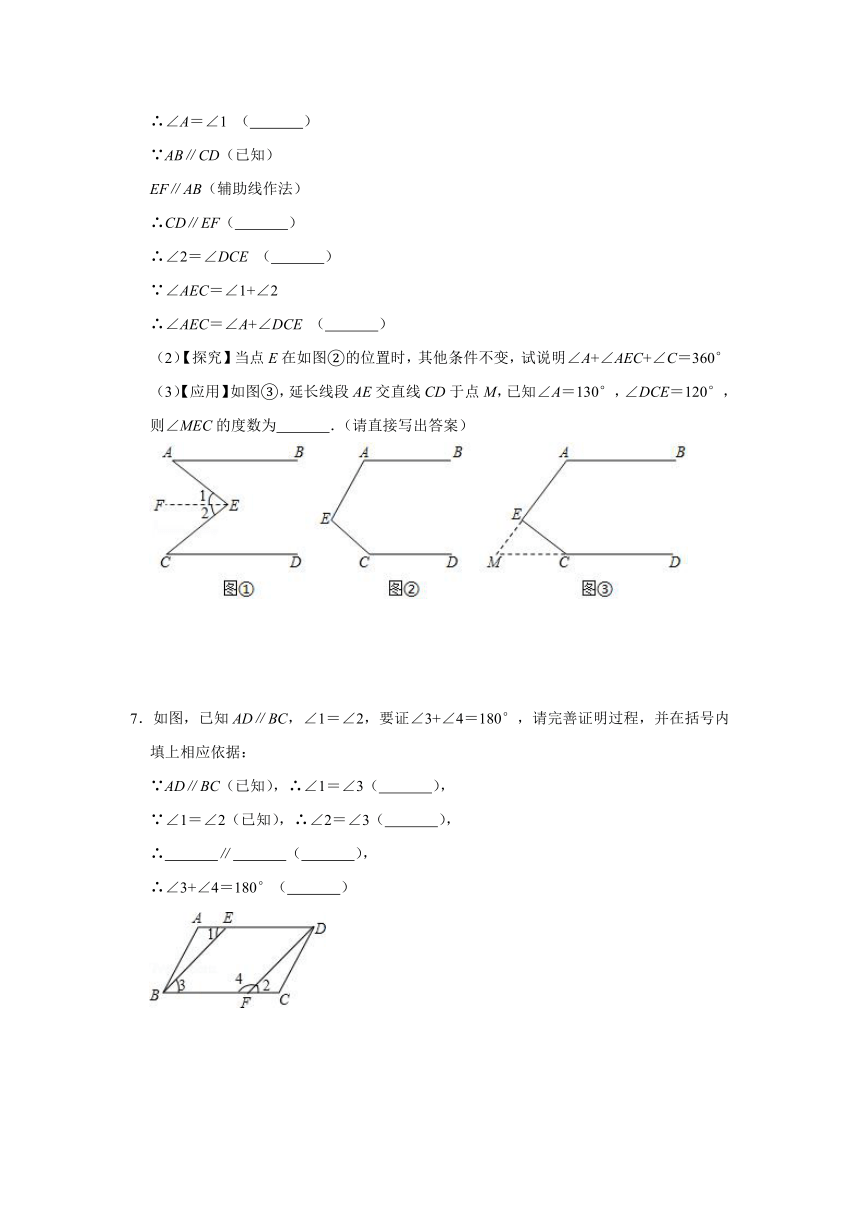
4.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).
5.如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
解:∵EF∥AD,(已知)
∴∠2=
.(
)
又∵∠1=∠2,(
)
∴∠1=∠3,(
)
∴AB∥
,(
)
∴∠DGA+∠BAC=180°.(
)
6.(1)【感知】如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE,试说明∠AEC=∠A+∠DCE.下面给出了这道题的解题过程,请完成下面的解题过程(填恰当的理由).
证明:如图①过点E作EF∥AB.
∴∠A=∠1
(
)
∵AB∥CD(已知)
EF∥AB(辅助线作法)
∴CD∥EF(
)
∴∠2=∠DCE
(
)
∵∠AEC=∠1+∠2
∴∠AEC=∠A+∠DCE
(
)
(2)【探究】当点E在如图②的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°
(3)【应用】如图③,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,则∠MEC的度数为
.(请直接写出答案)
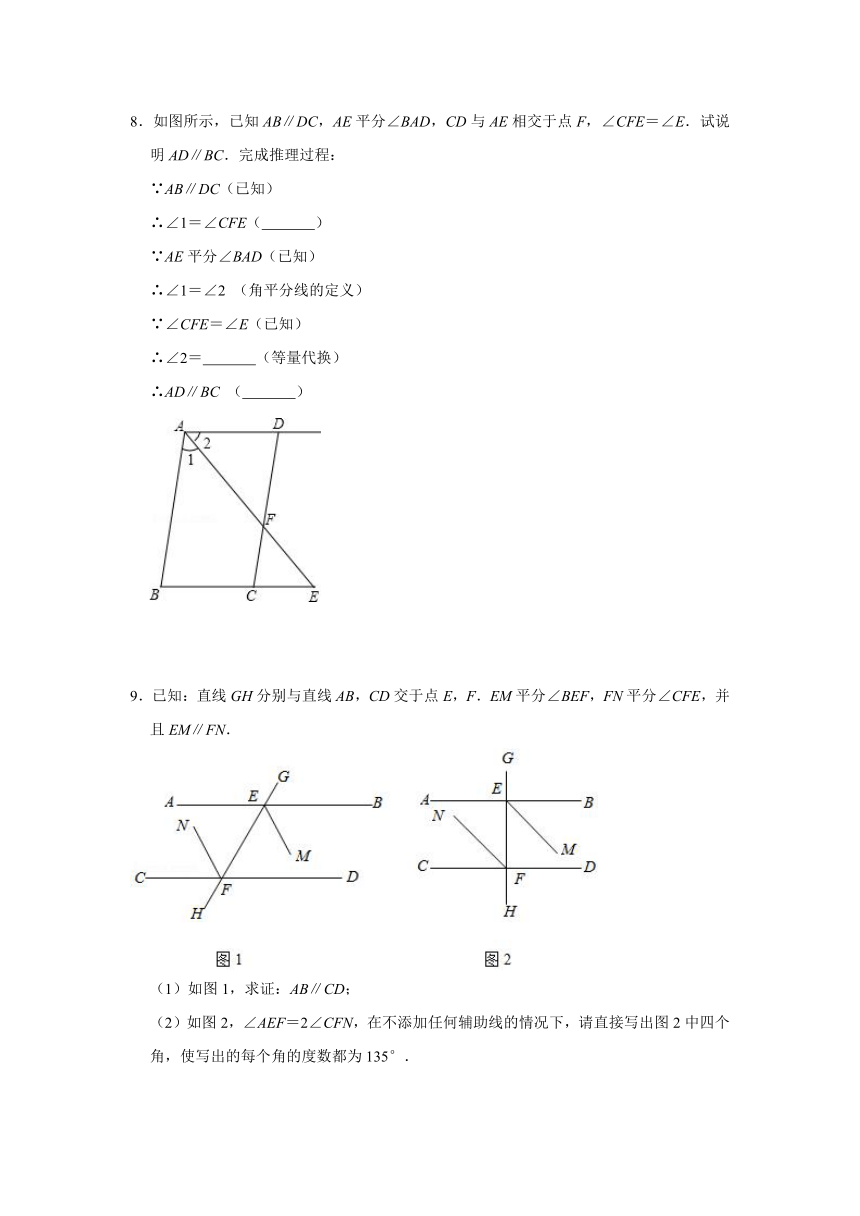
7.如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知),∴∠1=∠3(
),
∵∠1=∠2(已知),∴∠2=∠3(
),
∴
∥
(
),
∴∠3+∠4=180°(
)
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(
)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=
(等量代换)
∴AD∥BC
(
)
9.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
10.已知BE平分∠ABD,DE平分∠BDC,且∠BED=∠ABE+∠EDC.
(1)如图1,求证:AB∥CD;
(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求的值;
(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.
参考答案
1.解:(1)DE∥BC,理由如下:
∵FG∥AC,
∴∠FGB=∠C,
∵∠EDC+∠ADE=180°,∠FGC+∠FGB=180°,∠EDC=∠FGC,
∴∠ADE=∠FGB,
∴∠ADE=∠C,
∴DE∥BC;
(2)∵∠A=60°,∠C=55°,
∴∠B=180°﹣∠A﹣∠C=180°﹣60°﹣55°=65°,
∵FG∥AC,
∴∠FGB=∠C=55°,
∵∠FGM=4∠MGC,
∴∠FGM+∠MGC+∠FGB=5∠MGC+55°=180°,
∴∠MGN=25°,
∵MN∥AB,
∴∠MNC=∠B=65°,∠MNC=∠MGN+∠GMN,
∴∠GMN=∠MNC﹣∠MGN=65°﹣25°=40°;
(3)①如图②所示:
∵∠A=α,∠ACB=β,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣α﹣β,
∵FG∥AC,
∴∠FGB=∠C=β,
∵∠FGM=n∠MGC,
∴∠FGM+∠MGC+∠FGB=(n+1)∠MGC+β=180°,
∴∠MGN=,
∵MN∥AB,
∴∠MNC=∠B=180°﹣α﹣β,∠MNC=∠MGN+∠GMN,
∴∠GMN=∠MNC﹣∠MGN=180°﹣α﹣β﹣=(180°﹣β)﹣α.
②如图③所示:
设∠MGN=x,
则∠GMN=∠GMA+∠NMC=α+180°﹣nx,
∵(n﹣1)x+β=180°,
∴x=,
∴∠GMN=α+180°﹣nx=α+180°﹣n=α+.
2.解:(1)EF∥CD.理由如下:
∵∠1=∠2,∴AB∥EF,
∴∠AEF=∠MAE,又∠MAE=45°,∠FEG=15°,
∴∠AEG=60°,
∵EG平分∠AEC,∴∠CEG=∠AEG=60°,
∴∠CEF=∠CEG+∠FEG=75°,∠NCE=75°,
∴∠NCE=∠CEF,∴EF∥CD.
故EF与CD的位置关系是EF∥CD.
(2)∵∠1=∠2,∴AB∥EF,
∴∠FEA+∠MAE=180°,∠MAE=140°,
∴∠FEA=40°,∠FEG=30°,
∴∠AEG=70°,
∵EG平分∠AEC,∴∠CEG=∠AEG=70°,∴∠FEC=100°,
∵AB∥CD,∴EF∥CD,
∴∠NCE+∠FEC=180°∴∠NCE=80°.
答:∠NCE的度数为80°.
(3)∠MAE=2∠FEG+∠NCE时,AB∥CD.理由如下:
由(2)可知:∠AEG=180°﹣∠MAE+∠FEG,∠FEC=∠FEG+∠NCE,
∠AEG=∠FEC,∠FEC+∠NCE=180°
∴(180°﹣∠MAE+∠FEG)+(∠FEG+∠NCE)=180°,
整理得:∠MAE=2∠FEG+∠NCE.
故当∠MAE、∠FEG、∠NCE之间满足关系:∠MAE=2∠FEG+∠NCE时,AB∥CD.
3.证明:∵HG∥AB,(已知)
∴∠1=∠3. (
两直线平行、内错角相等)
∵HG∥CD(已知)
∴∠2=∠4. (两直线平行、内错角相等)
∵AB∥CD(已知)
∴∠BEF+∠EFD=180°(两直线平行、同旁内角互补)
∵EG平分∠BEF(已知)
∴∠1=∠BEF(角平分线的定义)
∵FG平分∠EFD(已知)
∴∠2=∠EFD(角平分线的定义)
∴∠1+∠2=?(∠BEF+∠EFD).
∴∠1+∠2=90°.
∴∠3+∠4=90°(
等量代换).
即∠EGF=90°.
故答案为:两直线平行、内错角相等;两直线平行、内错角相等;两直线平行、同旁内角互补,角平分线的定义;角平分线的定义;∠BEF;,∠EFD;等量代换.
4.解:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
5.解:∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG,(内错角相等,两直线平行)
∴∠DGA+∠BAC=180°(两直线平行,同旁内角互补).
6.(1)证明:如图①,过点E作EF∥AB,
∴∠A=∠1(两直线平行,内错角相等),
∵AB∥CD(已知),
∵EF∥AB(辅助线作法),
∴CD∥EF(平行于同一直线的两条直线平行),
∴∠2=∠DCE(两直线平行,内错角相等),
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
故答案为:两直线平行,内错角相等;平行于同一直线的两条直线平行;两直线平行,内错角相等;等量代换;
(2)证明:过点E作EF∥AB,如图②所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
(3)解:同(2)得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°,
故答案为:70°.
7.解:∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴BE∥DF(同位角相等,两直线平行),
∴∠3+∠4=180°
(两直线平行,同旁内角互补).
8.证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠E;内错角相等,两直线平行.
9.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
10.解:(1)如图1,延长BE交CD于点C,则∠BED=∠C+∠EDC.
∵∠BED=∠ABE+∠EDC,
∴∠ABE=∠C,
∴AB∥CD;
(2)由(1)可知,AB∥CD,
∴∠ABD+∠BDC=180°,
∵BE平分∠ABD,DE平分∠BDC,
∴∠BED=(∠ABD+∠BDC)=90°,
由∠ABE=3∠ABF,设∠ABF=α,则∠ABE=3α
过F作FG平行于AB,如图2,
则有∠ABF+∠CDF=∠F,
∴∠CDF=30°﹣α
过E作EH平行于AB,则有∠ABE+∠CDE=∠BED,
∴∠CDE=90°﹣3α,∴∠FDE=60°﹣2α
∴==;
(3)当点H在点D的左侧时,如图3所示,∠BHD=2∠EBI.
理由如下:
∵AB∥CD
∴∠ABH=∠BHD,
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABE=∠EBD,∠HBI=∠IBD
∵∠ABH=∠ABE+∠EBH=∠EBD+∠EBH=2(∠EBH+∠HBI),
∴∠BHD=2∠EBI.
当点H在点D的右侧时,如图4所示,∠EBI=90°﹣∠BHD.
理由如下:
∵AB∥CD
∴∠GBH=∠BHD,
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABE=∠EBD,∠HBI=∠IBD
∵∠EBI=∠EBD+∠DBI=∠ABD+∠DBH=∠ABH=(180°﹣∠HBG)
∴∠EBI=90°﹣∠BHD.
《
平面的图形认识(二)》(一)
1.已知,如图①,点D,E,F,G是△ABC三边上的点,且FG∥AC,
(1)若∠EDC=∠FGC,试判断DE与BC是否平行,并说明理由.
(2)如图②,点M、N分别在边AC、BC上,且MN∥AB,连结GM,若∠A=60°,∠C=55°,∠FGM=4∠MGC,求∠GMN的度数.
(3)点M、N分别在射线AC、BC上,且MN∥AB,连结GM.若∠A=α,∠ACB=β,∠FGM=n∠MGC,直接写出∠GMN的度数(用含α,β,n的代数式表示)
2.已知:∠1=∠2,EG平分∠AEC.
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.试判断EF与CD的位置关系,并说明理由.
(2)如图②,∠MAE=140°,∠FEG=30°,当AB∥CD时,求∠NCE的度数;
(3)如图②,试写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
3.完成下面的证明:如图AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.求证:∠EGF=90°.
证明:∵HG∥AB,(已知)
∴∠1=∠3. (
)
∵HG∥CD(已知)
∴∠2=∠4. (
)
∵AB∥CD(已知)
∴∠BEF+∠EFD=180°(
)
∵EG平分∠BEF(已知)
∴∠1=∠BEF(
)
∵FG平分∠EFD(已知)
∴∠2=∠EFD(
)
∴∠1+∠2=?(
+
).
∴∠1+∠2=90°.
∴∠3+∠4=90°(
).
即∠EGF=90°.
4.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).
5.如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
解:∵EF∥AD,(已知)
∴∠2=
.(
)
又∵∠1=∠2,(
)
∴∠1=∠3,(
)
∴AB∥
,(
)
∴∠DGA+∠BAC=180°.(
)
6.(1)【感知】如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE,试说明∠AEC=∠A+∠DCE.下面给出了这道题的解题过程,请完成下面的解题过程(填恰当的理由).
证明:如图①过点E作EF∥AB.
∴∠A=∠1
(
)
∵AB∥CD(已知)
EF∥AB(辅助线作法)
∴CD∥EF(
)
∴∠2=∠DCE
(
)
∵∠AEC=∠1+∠2
∴∠AEC=∠A+∠DCE
(
)
(2)【探究】当点E在如图②的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°
(3)【应用】如图③,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,则∠MEC的度数为
.(请直接写出答案)
7.如图,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知),∴∠1=∠3(
),
∵∠1=∠2(已知),∴∠2=∠3(
),
∴
∥
(
),
∴∠3+∠4=180°(
)
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(
)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=
(等量代换)
∴AD∥BC
(
)
9.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
10.已知BE平分∠ABD,DE平分∠BDC,且∠BED=∠ABE+∠EDC.
(1)如图1,求证:AB∥CD;
(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求的值;
(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.
参考答案
1.解:(1)DE∥BC,理由如下:
∵FG∥AC,
∴∠FGB=∠C,
∵∠EDC+∠ADE=180°,∠FGC+∠FGB=180°,∠EDC=∠FGC,
∴∠ADE=∠FGB,
∴∠ADE=∠C,
∴DE∥BC;
(2)∵∠A=60°,∠C=55°,
∴∠B=180°﹣∠A﹣∠C=180°﹣60°﹣55°=65°,
∵FG∥AC,
∴∠FGB=∠C=55°,
∵∠FGM=4∠MGC,
∴∠FGM+∠MGC+∠FGB=5∠MGC+55°=180°,
∴∠MGN=25°,
∵MN∥AB,
∴∠MNC=∠B=65°,∠MNC=∠MGN+∠GMN,
∴∠GMN=∠MNC﹣∠MGN=65°﹣25°=40°;
(3)①如图②所示:
∵∠A=α,∠ACB=β,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣α﹣β,
∵FG∥AC,
∴∠FGB=∠C=β,
∵∠FGM=n∠MGC,
∴∠FGM+∠MGC+∠FGB=(n+1)∠MGC+β=180°,
∴∠MGN=,
∵MN∥AB,
∴∠MNC=∠B=180°﹣α﹣β,∠MNC=∠MGN+∠GMN,
∴∠GMN=∠MNC﹣∠MGN=180°﹣α﹣β﹣=(180°﹣β)﹣α.
②如图③所示:
设∠MGN=x,
则∠GMN=∠GMA+∠NMC=α+180°﹣nx,
∵(n﹣1)x+β=180°,
∴x=,
∴∠GMN=α+180°﹣nx=α+180°﹣n=α+.
2.解:(1)EF∥CD.理由如下:
∵∠1=∠2,∴AB∥EF,
∴∠AEF=∠MAE,又∠MAE=45°,∠FEG=15°,
∴∠AEG=60°,
∵EG平分∠AEC,∴∠CEG=∠AEG=60°,
∴∠CEF=∠CEG+∠FEG=75°,∠NCE=75°,
∴∠NCE=∠CEF,∴EF∥CD.
故EF与CD的位置关系是EF∥CD.
(2)∵∠1=∠2,∴AB∥EF,
∴∠FEA+∠MAE=180°,∠MAE=140°,
∴∠FEA=40°,∠FEG=30°,
∴∠AEG=70°,
∵EG平分∠AEC,∴∠CEG=∠AEG=70°,∴∠FEC=100°,
∵AB∥CD,∴EF∥CD,
∴∠NCE+∠FEC=180°∴∠NCE=80°.
答:∠NCE的度数为80°.
(3)∠MAE=2∠FEG+∠NCE时,AB∥CD.理由如下:
由(2)可知:∠AEG=180°﹣∠MAE+∠FEG,∠FEC=∠FEG+∠NCE,
∠AEG=∠FEC,∠FEC+∠NCE=180°
∴(180°﹣∠MAE+∠FEG)+(∠FEG+∠NCE)=180°,
整理得:∠MAE=2∠FEG+∠NCE.
故当∠MAE、∠FEG、∠NCE之间满足关系:∠MAE=2∠FEG+∠NCE时,AB∥CD.
3.证明:∵HG∥AB,(已知)
∴∠1=∠3. (
两直线平行、内错角相等)
∵HG∥CD(已知)
∴∠2=∠4. (两直线平行、内错角相等)
∵AB∥CD(已知)
∴∠BEF+∠EFD=180°(两直线平行、同旁内角互补)
∵EG平分∠BEF(已知)
∴∠1=∠BEF(角平分线的定义)
∵FG平分∠EFD(已知)
∴∠2=∠EFD(角平分线的定义)
∴∠1+∠2=?(∠BEF+∠EFD).
∴∠1+∠2=90°.
∴∠3+∠4=90°(
等量代换).
即∠EGF=90°.
故答案为:两直线平行、内错角相等;两直线平行、内错角相等;两直线平行、同旁内角互补,角平分线的定义;角平分线的定义;∠BEF;,∠EFD;等量代换.
4.解:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
5.解:∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG,(内错角相等,两直线平行)
∴∠DGA+∠BAC=180°(两直线平行,同旁内角互补).
6.(1)证明:如图①,过点E作EF∥AB,
∴∠A=∠1(两直线平行,内错角相等),
∵AB∥CD(已知),
∵EF∥AB(辅助线作法),
∴CD∥EF(平行于同一直线的两条直线平行),
∴∠2=∠DCE(两直线平行,内错角相等),
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
故答案为:两直线平行,内错角相等;平行于同一直线的两条直线平行;两直线平行,内错角相等;等量代换;
(2)证明:过点E作EF∥AB,如图②所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
(3)解:同(2)得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°,
故答案为:70°.
7.解:∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴BE∥DF(同位角相等,两直线平行),
∴∠3+∠4=180°
(两直线平行,同旁内角互补).
8.证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠E;内错角相等,两直线平行.
9.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
10.解:(1)如图1,延长BE交CD于点C,则∠BED=∠C+∠EDC.
∵∠BED=∠ABE+∠EDC,
∴∠ABE=∠C,
∴AB∥CD;
(2)由(1)可知,AB∥CD,
∴∠ABD+∠BDC=180°,
∵BE平分∠ABD,DE平分∠BDC,
∴∠BED=(∠ABD+∠BDC)=90°,
由∠ABE=3∠ABF,设∠ABF=α,则∠ABE=3α
过F作FG平行于AB,如图2,
则有∠ABF+∠CDF=∠F,
∴∠CDF=30°﹣α
过E作EH平行于AB,则有∠ABE+∠CDE=∠BED,
∴∠CDE=90°﹣3α,∴∠FDE=60°﹣2α
∴==;
(3)当点H在点D的左侧时,如图3所示,∠BHD=2∠EBI.
理由如下:
∵AB∥CD
∴∠ABH=∠BHD,
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABE=∠EBD,∠HBI=∠IBD
∵∠ABH=∠ABE+∠EBH=∠EBD+∠EBH=2(∠EBH+∠HBI),
∴∠BHD=2∠EBI.
当点H在点D的右侧时,如图4所示,∠EBI=90°﹣∠BHD.
理由如下:
∵AB∥CD
∴∠GBH=∠BHD,
∵BE平分∠ABD,BI平分∠HBD,
∴∠ABE=∠EBD,∠HBI=∠IBD
∵∠EBI=∠EBD+∠DBI=∠ABD+∠DBH=∠ABH=(180°﹣∠HBG)
∴∠EBI=90°﹣∠BHD.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
