数学人教A版选修2-2-1.1.3 导数的几何意义(16张PPT)
文档属性
| 名称 | 数学人教A版选修2-2-1.1.3 导数的几何意义(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 10:13:22 | ||
图片预览



文档简介
1.1.3 导数的几何意义
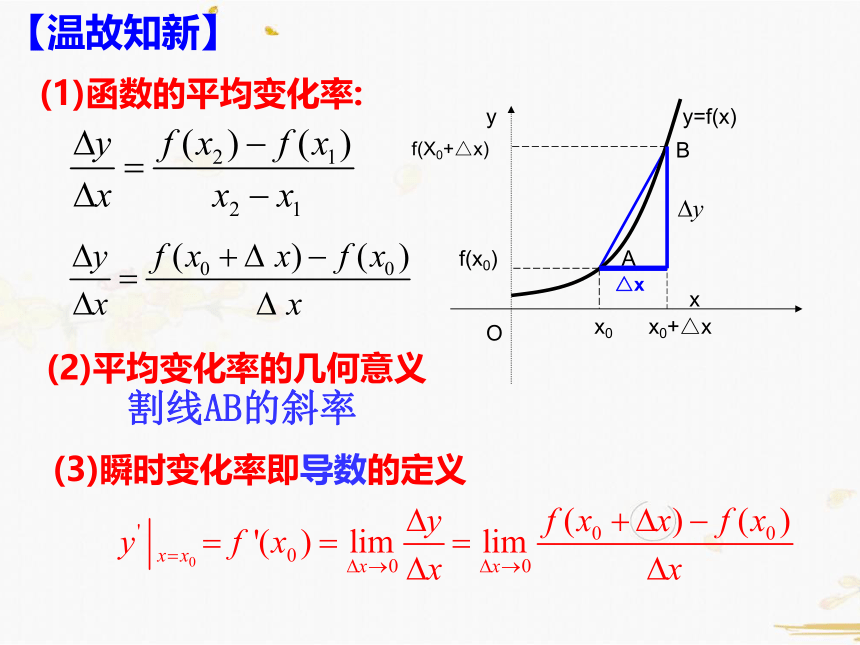
(1)函数的平均变化率:
【温故知新】
(2)平均变化率的几何意义
O
A
B
x
y
y=f(x)
x0
x0+△x
f(x0)
f(X0+△x)
△x
(3)瞬时变化率即导数的定义
割线AB的斜率
求函数y=f(x)在点x0处的导数的基本方法是:
注意:这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.
P
l
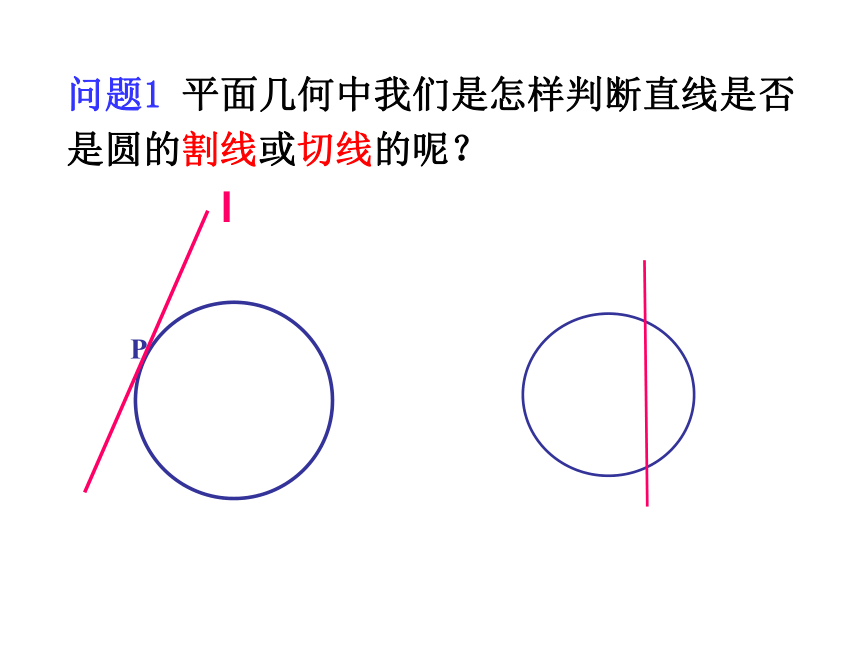
问题1 平面几何中我们是怎样判断直线是否
是圆的割线或切线的呢?
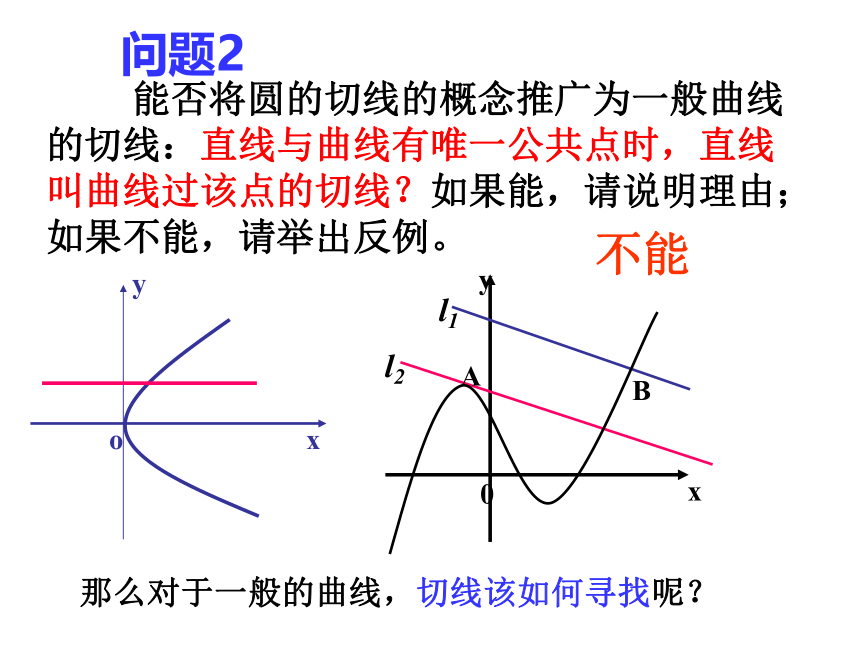
问题2
能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。
不能
x
y
o
l2
l1
A
B
0
x
y
那么对于一般的曲线,切线该如何寻找呢?
P
Pn
o
x
y
y=f(x)
割线
切线
T
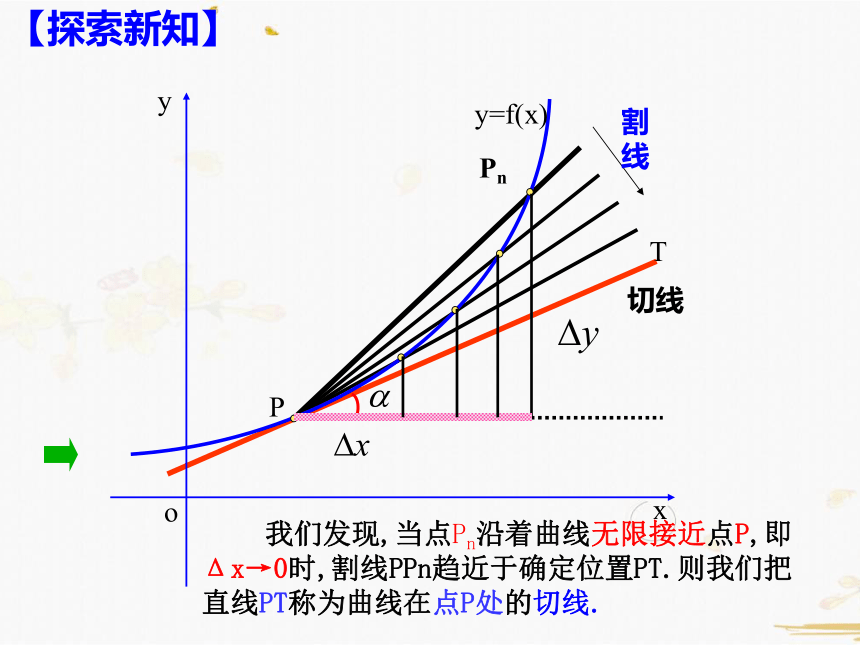
我们发现,当点Pn沿着曲线无限接近点P,即Δx→0时,割线PPn趋近于确定位置PT.则我们把直线PT称为曲线在点P处的切线.
【探索新知】
当Δx→0时,割线 PPn的斜率,称为曲线在点P处的切线的斜率.
即:
①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质——函数在x=x0处的导数.
P
Q
o
x
y
割线
切线
T
因此,函数f(x)在x=x0处的
导数就是切线PT的斜率.
【概念形成】
概念用途:
要注意,曲线在某点处的切线:
(1)与该点的位置有关;
(2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
(3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
例1:求曲线y=x2+1在点P(1,2)处的切线斜率及切线方程.
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
因此,切线的斜率k=2
切线方程为y-2=2(x-1),即y=2x.
求曲线上某点处的切线方程的步骤:
①求出函数y=f(x)在点x0处的导数f’(x0);
②利用点斜式求切线方程。
【典例精析】
若点不在曲线上呢?
例2:试求过点 且与曲线 相切的直线方程。
切线斜率:
解得
切点为
直线方程
即
解:因为点 不在曲线上,设此切线过抛物线上的切点为 ,则
思路:
设出切点利用导数的几何意义和已知条件去求
在不致发生混淆时,导函数也简称导数。
导函数
由函数f(x)在x=x0处求导数的过程可以看到,当x=x0时,f’(x0) 是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:
课后练 习:
(1)求出函数在点x0处的导数 ,即为曲线
在点(x0,f(x0))的切线的斜率。
(2)根据直线方程的点斜式写出切线方程,即
1.求切线方程的步骤:
小结:
作业布置
P
E
C
D
B
A
1、如图:在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点。
(1)证明:PA//平面EDB;
(2)求EB与底面ABCD所成角的正切值。
作业布置
2、设△ABC的内角A,B,C所对边的长分别是a,b,c,且
b=3,c=1,A=2B.
(1)求a的值;
(2)求 的值.
(1)函数的平均变化率:
【温故知新】
(2)平均变化率的几何意义
O
A
B
x
y
y=f(x)
x0
x0+△x
f(x0)
f(X0+△x)
△x
(3)瞬时变化率即导数的定义
割线AB的斜率
求函数y=f(x)在点x0处的导数的基本方法是:
注意:这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.
P
l
问题1 平面几何中我们是怎样判断直线是否
是圆的割线或切线的呢?
问题2
能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。
不能
x
y
o
l2
l1
A
B
0
x
y
那么对于一般的曲线,切线该如何寻找呢?
P
Pn
o
x
y
y=f(x)
割线
切线
T
我们发现,当点Pn沿着曲线无限接近点P,即Δx→0时,割线PPn趋近于确定位置PT.则我们把直线PT称为曲线在点P处的切线.
【探索新知】
当Δx→0时,割线 PPn的斜率,称为曲线在点P处的切线的斜率.
即:
①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质——函数在x=x0处的导数.
P
Q
o
x
y
割线
切线
T
因此,函数f(x)在x=x0处的
导数就是切线PT的斜率.
【概念形成】
概念用途:
要注意,曲线在某点处的切线:
(1)与该点的位置有关;
(2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
(3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
例1:求曲线y=x2+1在点P(1,2)处的切线斜率及切线方程.
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
因此,切线的斜率k=2
切线方程为y-2=2(x-1),即y=2x.
求曲线上某点处的切线方程的步骤:
①求出函数y=f(x)在点x0处的导数f’(x0);
②利用点斜式求切线方程。
【典例精析】
若点不在曲线上呢?
例2:试求过点 且与曲线 相切的直线方程。
切线斜率:
解得
切点为
直线方程
即
解:因为点 不在曲线上,设此切线过抛物线上的切点为 ,则
思路:
设出切点利用导数的几何意义和已知条件去求
在不致发生混淆时,导函数也简称导数。
导函数
由函数f(x)在x=x0处求导数的过程可以看到,当x=x0时,f’(x0) 是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:
课后练 习:
(1)求出函数在点x0处的导数 ,即为曲线
在点(x0,f(x0))的切线的斜率。
(2)根据直线方程的点斜式写出切线方程,即
1.求切线方程的步骤:
小结:
作业布置
P
E
C
D
B
A
1、如图:在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点。
(1)证明:PA//平面EDB;
(2)求EB与底面ABCD所成角的正切值。
作业布置
2、设△ABC的内角A,B,C所对边的长分别是a,b,c,且
b=3,c=1,A=2B.
(1)求a的值;
(2)求 的值.
