数学人教A版选修2-2-1.2导数的计算(33张PPT)
文档属性
| 名称 | 数学人教A版选修2-2-1.2导数的计算(33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 845.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 09:56:54 | ||
图片预览










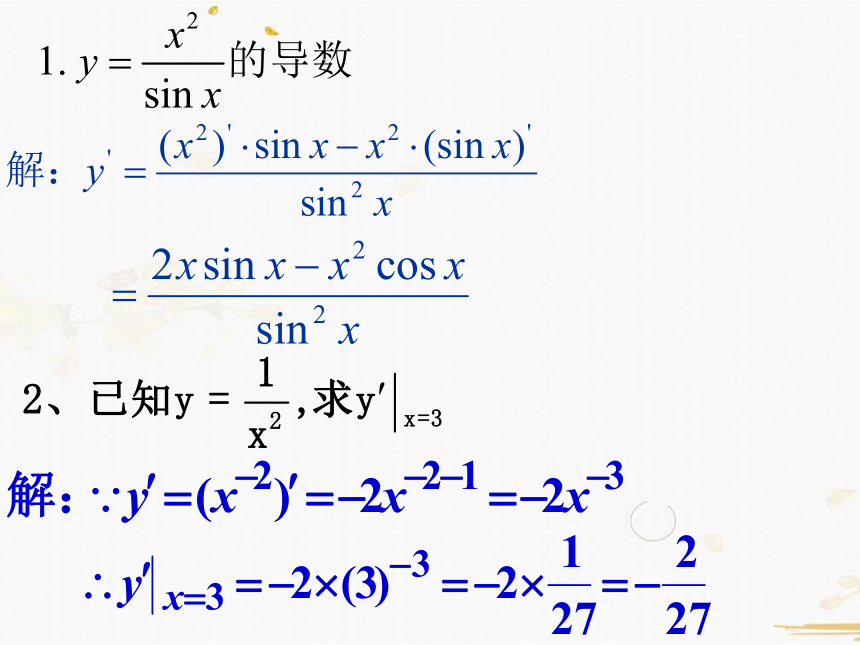

文档简介
1.2 导数的计算
第一课时
例.用导数的定义求下列各函数的导数:
(3)f(x)=x2
(4)f(x)=x3
几种常见函数的导数
基本初等函数求导公式:
例:求下列函数的导数
例题讲解
导数的四则运算法则
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
应用1: 求下列函数的导数
(1)y=x3+sinx
(2)y=x4-x2-x+3.
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
应用2:求下列函数的导数
(1)y=(2x2+3)(3x-2)
(2)y=(1+x6)(2+sinx)
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
应用3:求下列函数的导数
(1)y=tanx
做P18练习第2题:
(1)——(4)
课后练习
例:求曲线y=x3+3x-8在x=2
处的切线的方程.
典例讲解
练习:求曲线y=cosx在点P( ) 处的切线的直线方程.
1.2 导数的计算
第二课时
函数
导数
y=c
y=xn (n是有理数)
y=sinx
y=cosx
y=ax
y=ex
y=logax
y=lnx
导数的运算法则:
课后练习
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
如下函数由多少个函数复合而成:
例4、 求下列函数的导数
总结:
函数求导的基本步骤:
1,分析函数的结构和特征
2,选择恰当的求导法则和导数公式
3,整理得到结果
做P18 练习第2题(5)(6)
作业布置
1、P18 A组 第4—7题
2、预习 1.3.1内容
2、若直线y=3x+1是曲线y=ax3的切线,试求a的值.
提高练习
1、求曲线y=x3+3x-8在x=2
处的切线的方程.
1、求曲线y=x3+3x-8在x=2
处的切线的方程.
提高练习
2、若直线y=3x+1是曲线y=ax3的切线,试求a的值.
解:设直线y=3x+1与曲线y=ax3相切于点P(x0,y0),则有: y0=3x0+1 ①
y0=ax03 ②
3ax02=3 ③
由①,②得3x0+1=ax03,由③得ax02=1,代入上式可得:3x0+1=x0,x0=-1/2.
所以 a?(-1/2)2=1,
即:a=4
提高练习
第一课时
例.用导数的定义求下列各函数的导数:
(3)f(x)=x2
(4)f(x)=x3
几种常见函数的导数
基本初等函数求导公式:
例:求下列函数的导数
例题讲解
导数的四则运算法则
法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:
应用1: 求下列函数的导数
(1)y=x3+sinx
(2)y=x4-x2-x+3.
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
应用2:求下列函数的导数
(1)y=(2x2+3)(3x-2)
(2)y=(1+x6)(2+sinx)
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
应用3:求下列函数的导数
(1)y=tanx
做P18练习第2题:
(1)——(4)
课后练习
例:求曲线y=x3+3x-8在x=2
处的切线的方程.
典例讲解
练习:求曲线y=cosx在点P( ) 处的切线的直线方程.
1.2 导数的计算
第二课时
函数
导数
y=c
y=xn (n是有理数)
y=sinx
y=cosx
y=ax
y=ex
y=logax
y=lnx
导数的运算法则:
课后练习
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
如下函数由多少个函数复合而成:
例4、 求下列函数的导数
总结:
函数求导的基本步骤:
1,分析函数的结构和特征
2,选择恰当的求导法则和导数公式
3,整理得到结果
做P18 练习第2题(5)(6)
作业布置
1、P18 A组 第4—7题
2、预习 1.3.1内容
2、若直线y=3x+1是曲线y=ax3的切线,试求a的值.
提高练习
1、求曲线y=x3+3x-8在x=2
处的切线的方程.
1、求曲线y=x3+3x-8在x=2
处的切线的方程.
提高练习
2、若直线y=3x+1是曲线y=ax3的切线,试求a的值.
解:设直线y=3x+1与曲线y=ax3相切于点P(x0,y0),则有: y0=3x0+1 ①
y0=ax03 ②
3ax02=3 ③
由①,②得3x0+1=ax03,由③得ax02=1,代入上式可得:3x0+1=x0,x0=-1/2.
所以 a?(-1/2)2=1,
即:a=4
提高练习
