数学人教A版选修2-2-1.3.2 函数的极值与导数(18张PPT)
文档属性
| 名称 | 数学人教A版选修2-2-1.3.2 函数的极值与导数(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 10:00:03 | ||
图片预览





文档简介
1.3.2 函数的极值与 导数
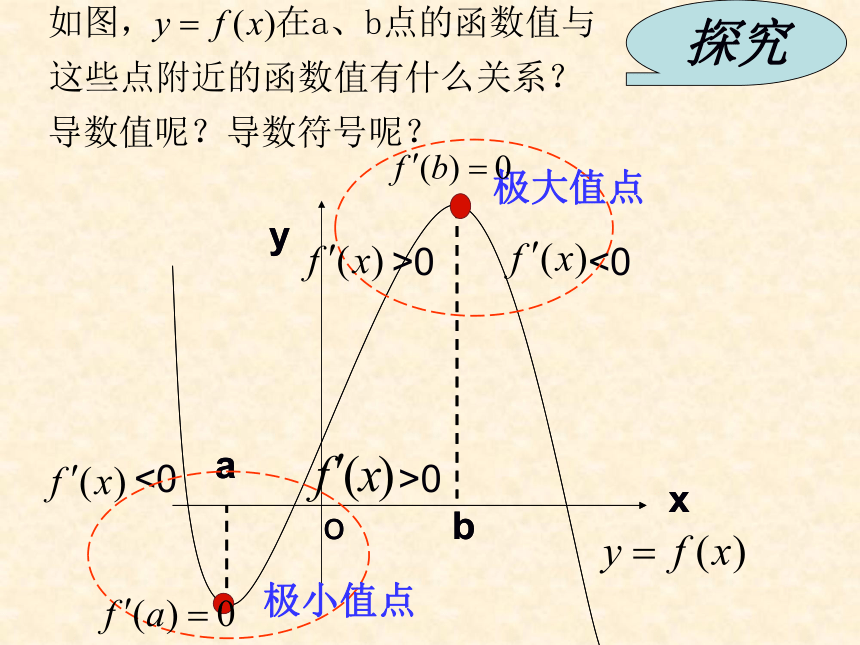
探究
x
y
o
a
b
x
y
o
a
b
>0
<0
<0
>0
极小值点
极大值点
函数的极值定义
一般的,设函数f(x)在点x0附近有定义,
如果对x0附近的所有点,都有f(x)则f(x0) 是函数f(x)的一个极大值, 记作y极大值= f(x0);
如果对x0附近的所有点,都有f(x)>f(x0),
则f(x0) 是函数f(x)的一个极小值,记作y极小值= f(x0);
使函数取得极值的点x0称为极值点
极小值点、极大值点统称为极值点, 极大值和极小值统称为极值.
(1)极值是某一点附近的小区间而言的,是函数的局部性质,不一定是整体的最值;
(2)极值点是自变量的值,极值指的是函数值;
(3)函数的极大(小)值可能不止一个,而且函数的极大值未必大于极小值;
【关于极值概念的几点说明】
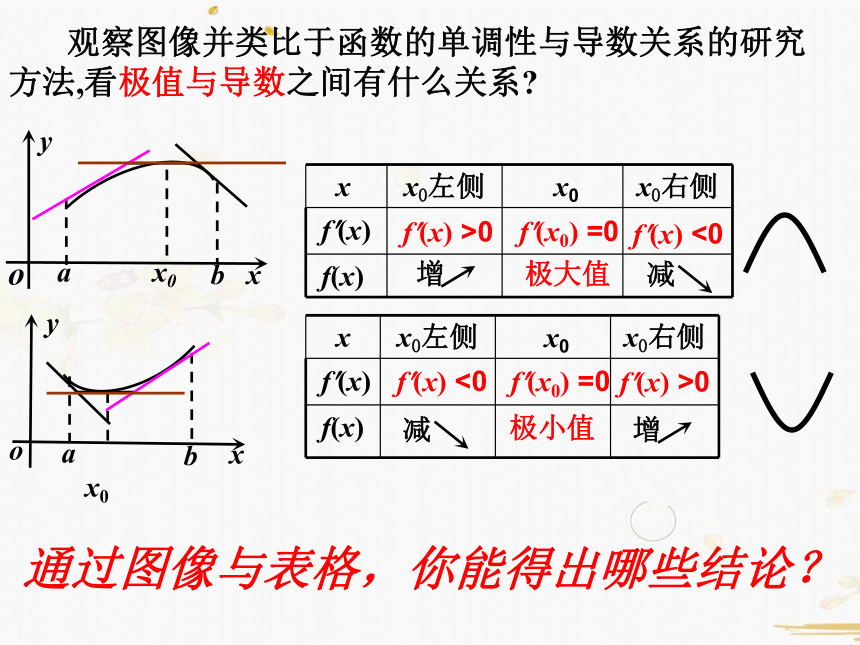
观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
增
f?(x) >0
f?(x0) =0
f?(x) <0
极大值
减
f?(x) <0
f?(x0) =0
增
减
极小值
f?(x) >0
通过图像与表格,你能得出哪些结论?
1、若x0是极值点(即f(x0) 是极值),则f ’(x0)=0。
2、若f ’(x0)=0,x0不一定是极值点,只有f?(x0) =0 且x0两侧f(x)单调性不同时,x0才是极值点.
3、y=f(x)在某一点的导数为0是函数y=f(x)在这点取得极值的 必要条件。
结论
课本P29练习1
解: ∵ f?(x)=x2-4,由f?(x) =0解得 x1=2,x2=-2.
∴ 当x=2时,y极小值=28/3;当x=-2时, y极大值=-4/3.
f(x)
f?(x)
x
(-∞,-2)
-2
(-2,2)
2
(2,+∞)
+
0
0
-
+
极大值28/3
极小值-4/3
当x变化时, f?(x) 、 f(x)的变化情况如下表:
请概括求可导函数的极大(小)值的步骤:
求函数极值(极大值,极小值)的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
若f ’(x0)左正右负,则f(x0)为极大值;
若 f ’(x0)左负右正,则f(x0)为极小值
+
-
x0
-
+
x0
简记:
求导—求极值点—列表—求极值
作业布置:
2、已知函数 在
处取得极值。
(1)求函数 的解析式
(2)求函数 的单调区间
1、求函数 的极值
P29 练习第2题
必要条件
函数极值与导数
函数极值的定义
函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.
函数极值的求法
求极值的步骤:1.求导,2.求极值点,3.列表,4.求极值
小结
P29 练习第2题
求下列函数的极值:
解:
令 解得 列表:
x
0
f (x)
+
单调递增
单调递减
–
所以, 当 时, f (x)有极小值
求下列函数的极值:
解:
解得 列表:
x
(–∞, –3)
–3
(–3, 3)
3
( 3, +∞)
0
0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –3 时, f (x)有极大值 54 ;
当 x = 3 时, f (x)有极小值 – 54 .
P29 练习第2题
求下列函数的极值:
解:
解得
所以, 当 x = –2 时, f (x)有极小值 – 10 ;
当 x = 2 时, f (x)有极大值 22 .
解得
所以, 当 x = –1 时, f (x)有极小值 – 2 ;
当 x = 1 时, f (x)有极大值 2 .
P29 练习第2题
1、求函数 的极值
x
(-∞,-1)
-1
(-1,0)
(0 , 1)
1
(1,+∞)
+
0
-
-
0
+
所以,当x=-1时,函数的极大值是-2,当x=1时,函数的极小值是2
导函数的正负是
交替出现的吗?
不是
极大值
极小值
作业布置:
2、已知函数 在 处取得极值:(1)求函数 的解析式
(2)求函数 的单调区间
2.(2006年天津卷)函数 的定义域为开区间
导函数 在 内的图像如图所示,则函数
在开区间 内有( )个极小值点。
巩固练习:
1.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 .
(A)1 (B)2 (C)3 (D) 4
3.已知函数f(x)=x3+ax2+bx+c,当x=-1时取得极大值7;当x=3时取得极小值,求这个极小值及a、b、c的值。
2.(2006年天津卷)函数 的定义域为开区间
导函数 在 内的图像如图所示,则函数
在开区间 内有( )个极小值点。
巩固练习:
1.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 .
(A)1 (B)2 (C)3 (D) 4
3.已知函数f(x)=x3+ax2+bx+c,当x=-1时取得极大值7;当x=3时取得极小值,求这个极小值及a、b、c的值。
a= -3,b= -9,c= 2,f(x)极小值= -25
探究
x
y
o
a
b
x
y
o
a
b
>0
<0
<0
>0
极小值点
极大值点
函数的极值定义
一般的,设函数f(x)在点x0附近有定义,
如果对x0附近的所有点,都有f(x)
如果对x0附近的所有点,都有f(x)>f(x0),
则f(x0) 是函数f(x)的一个极小值,记作y极小值= f(x0);
使函数取得极值的点x0称为极值点
极小值点、极大值点统称为极值点, 极大值和极小值统称为极值.
(1)极值是某一点附近的小区间而言的,是函数的局部性质,不一定是整体的最值;
(2)极值点是自变量的值,极值指的是函数值;
(3)函数的极大(小)值可能不止一个,而且函数的极大值未必大于极小值;
【关于极值概念的几点说明】
观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
o
a
x0
b
x
y
x
x0左侧
x0
x0右侧
f?(x)
f(x)
增
f?(x) >0
f?(x0) =0
f?(x) <0
极大值
减
f?(x) <0
f?(x0) =0
增
减
极小值
f?(x) >0
通过图像与表格,你能得出哪些结论?
1、若x0是极值点(即f(x0) 是极值),则f ’(x0)=0。
2、若f ’(x0)=0,x0不一定是极值点,只有f?(x0) =0 且x0两侧f(x)单调性不同时,x0才是极值点.
3、y=f(x)在某一点的导数为0是函数y=f(x)在这点取得极值的 必要条件。
结论
课本P29练习1
解: ∵ f?(x)=x2-4,由f?(x) =0解得 x1=2,x2=-2.
∴ 当x=2时,y极小值=28/3;当x=-2时, y极大值=-4/3.
f(x)
f?(x)
x
(-∞,-2)
-2
(-2,2)
2
(2,+∞)
+
0
0
-
+
极大值28/3
极小值-4/3
当x变化时, f?(x) 、 f(x)的变化情况如下表:
请概括求可导函数的极大(小)值的步骤:
求函数极值(极大值,极小值)的一般步骤:
(1)确定函数的定义域
(2)求方程f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f’(x)在方程f’(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
若f ’(x0)左正右负,则f(x0)为极大值;
若 f ’(x0)左负右正,则f(x0)为极小值
+
-
x0
-
+
x0
简记:
求导—求极值点—列表—求极值
作业布置:
2、已知函数 在
处取得极值。
(1)求函数 的解析式
(2)求函数 的单调区间
1、求函数 的极值
P29 练习第2题
必要条件
函数极值与导数
函数极值的定义
函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.
函数极值的求法
求极值的步骤:1.求导,2.求极值点,3.列表,4.求极值
小结
P29 练习第2题
求下列函数的极值:
解:
令 解得 列表:
x
0
f (x)
+
单调递增
单调递减
–
所以, 当 时, f (x)有极小值
求下列函数的极值:
解:
解得 列表:
x
(–∞, –3)
–3
(–3, 3)
3
( 3, +∞)
0
0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以, 当 x = –3 时, f (x)有极大值 54 ;
当 x = 3 时, f (x)有极小值 – 54 .
P29 练习第2题
求下列函数的极值:
解:
解得
所以, 当 x = –2 时, f (x)有极小值 – 10 ;
当 x = 2 时, f (x)有极大值 22 .
解得
所以, 当 x = –1 时, f (x)有极小值 – 2 ;
当 x = 1 时, f (x)有极大值 2 .
P29 练习第2题
1、求函数 的极值
x
(-∞,-1)
-1
(-1,0)
(0 , 1)
1
(1,+∞)
+
0
-
-
0
+
所以,当x=-1时,函数的极大值是-2,当x=1时,函数的极小值是2
导函数的正负是
交替出现的吗?
不是
极大值
极小值
作业布置:
2、已知函数 在 处取得极值:(1)求函数 的解析式
(2)求函数 的单调区间
2.(2006年天津卷)函数 的定义域为开区间
导函数 在 内的图像如图所示,则函数
在开区间 内有( )个极小值点。
巩固练习:
1.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 .
(A)1 (B)2 (C)3 (D) 4
3.已知函数f(x)=x3+ax2+bx+c,当x=-1时取得极大值7;当x=3时取得极小值,求这个极小值及a、b、c的值。
2.(2006年天津卷)函数 的定义域为开区间
导函数 在 内的图像如图所示,则函数
在开区间 内有( )个极小值点。
巩固练习:
1.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值,又有极小值,则a的取值范围为 .
(A)1 (B)2 (C)3 (D) 4
3.已知函数f(x)=x3+ax2+bx+c,当x=-1时取得极大值7;当x=3时取得极小值,求这个极小值及a、b、c的值。
a= -3,b= -9,c= 2,f(x)极小值= -25
