数学人教A版选修2-2-1.5.1-1.5.3定积分的概念(30张PPT)
文档属性
| 名称 | 数学人教A版选修2-2-1.5.1-1.5.3定积分的概念(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-27 00:00:00 | ||
图片预览

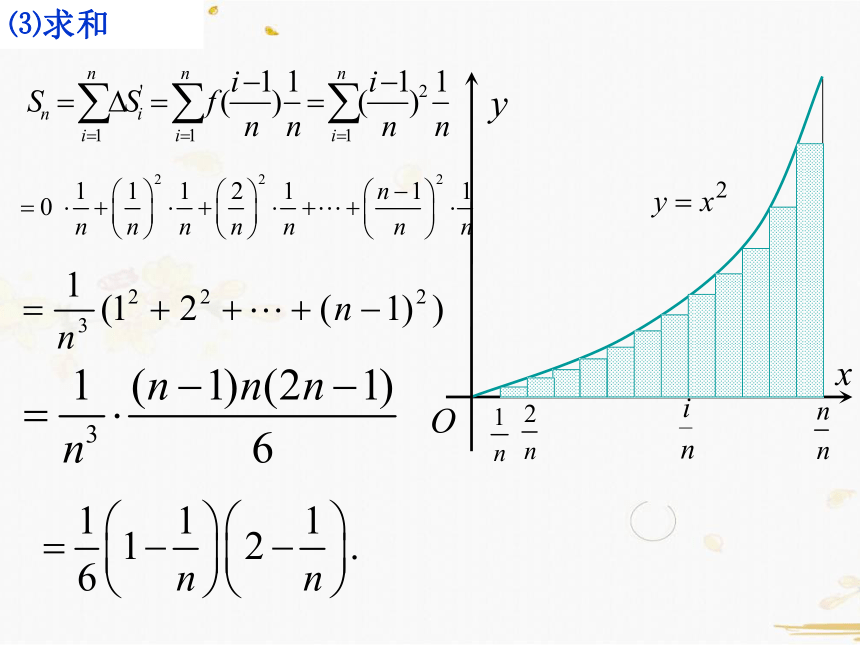


文档简介
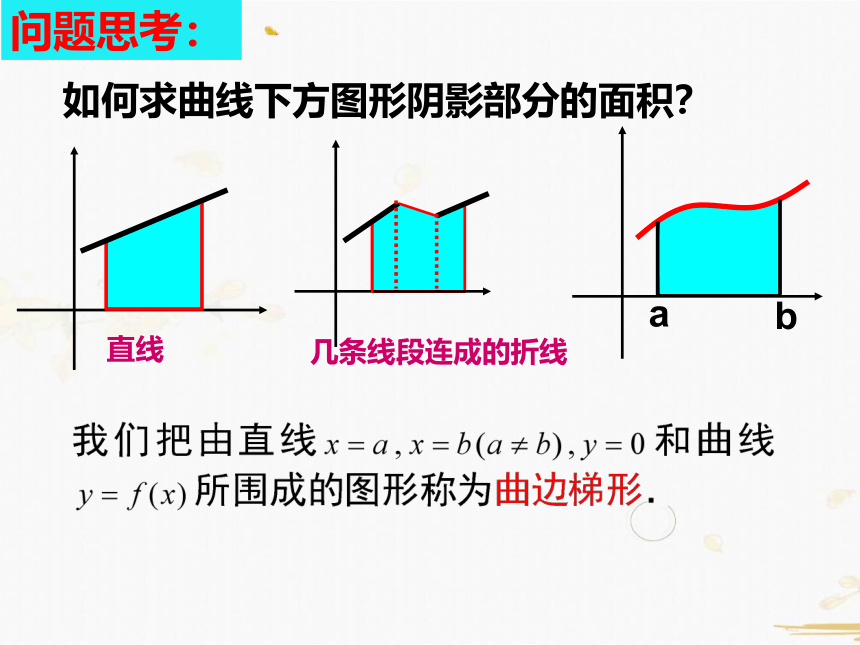
如何求曲线下方图形阴影部分的面积?
直线
几条线段连成的折线
问题思考:
a
b
y = f(x)
b
a
x
y
O
A1
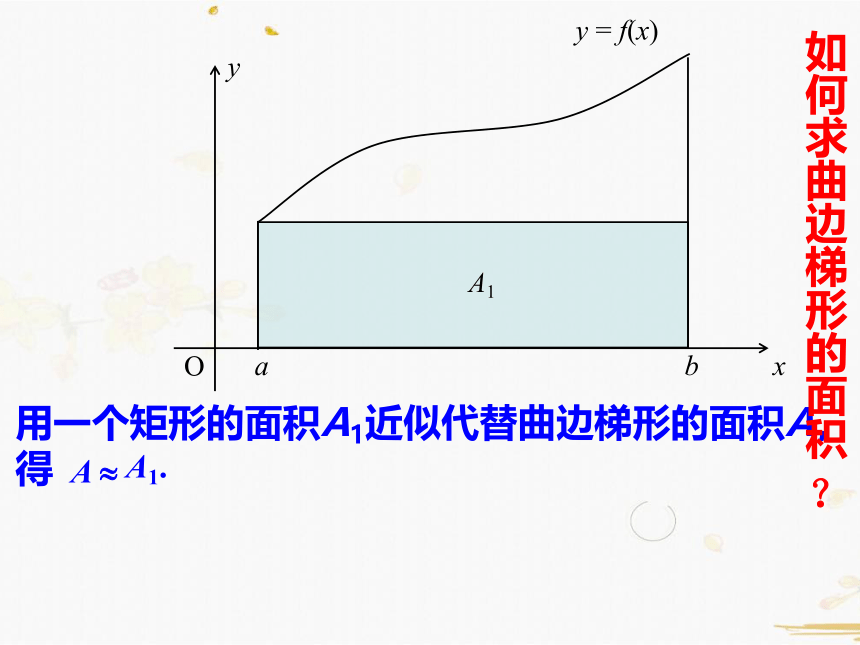
A ?
A1.
用一个矩形的面积A1近似代替曲边梯形的面积A,
得
如何求曲边梯形的面积
?
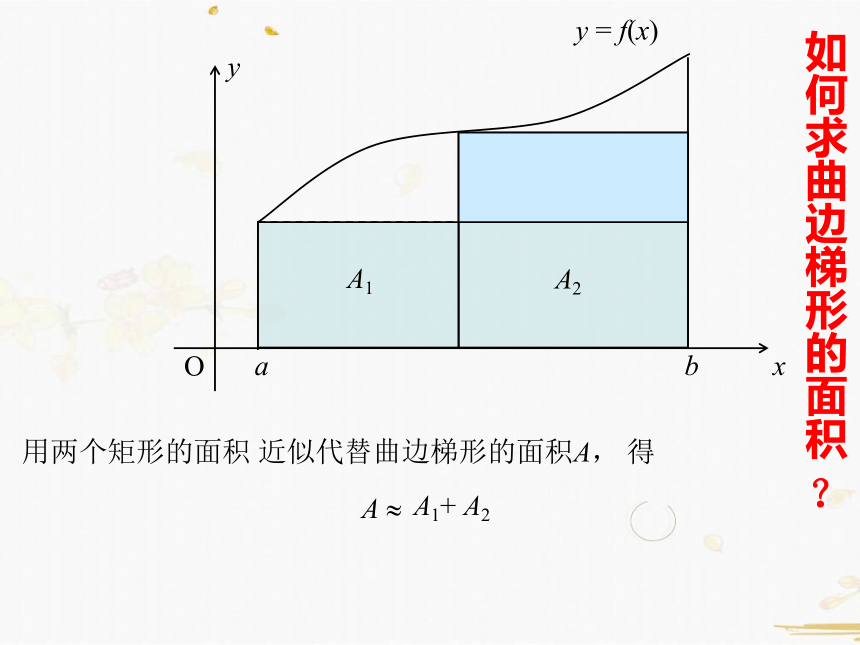
A ?
A1+ A2
用两个矩形的面积 近似代替曲边梯形的面积A, 得
y = f(x)
b
a
x
y
O
A1
A2
如何求曲边梯形的面积
?
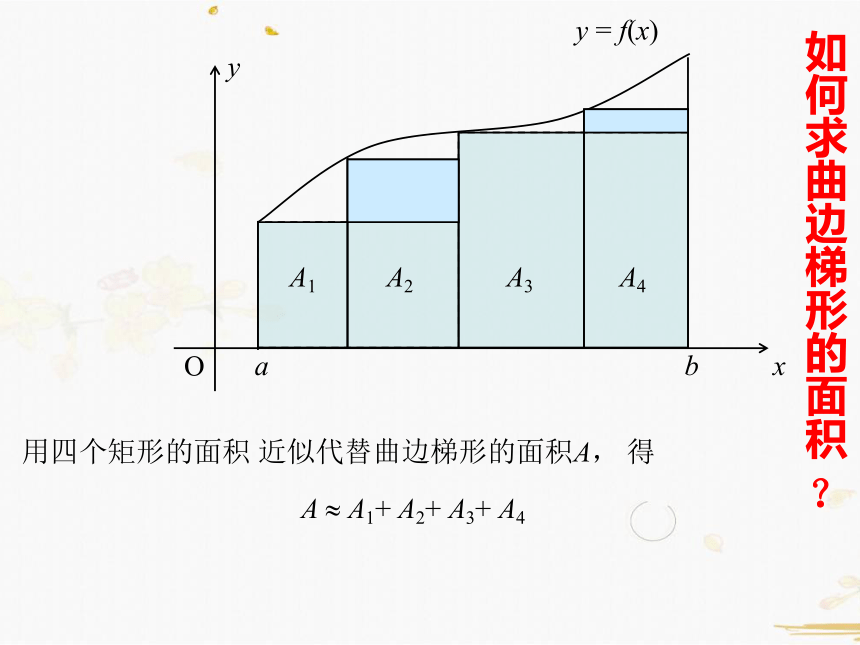
A ? A1+ A2+ A3+ A4
用四个矩形的面积 近似代替曲边梯形的面积A, 得
y = f(x)
b
a
x
y
O
A1
A2
A3
A4
如何求曲边梯形的面积
?
y = f(x)
b
a
x
y
O
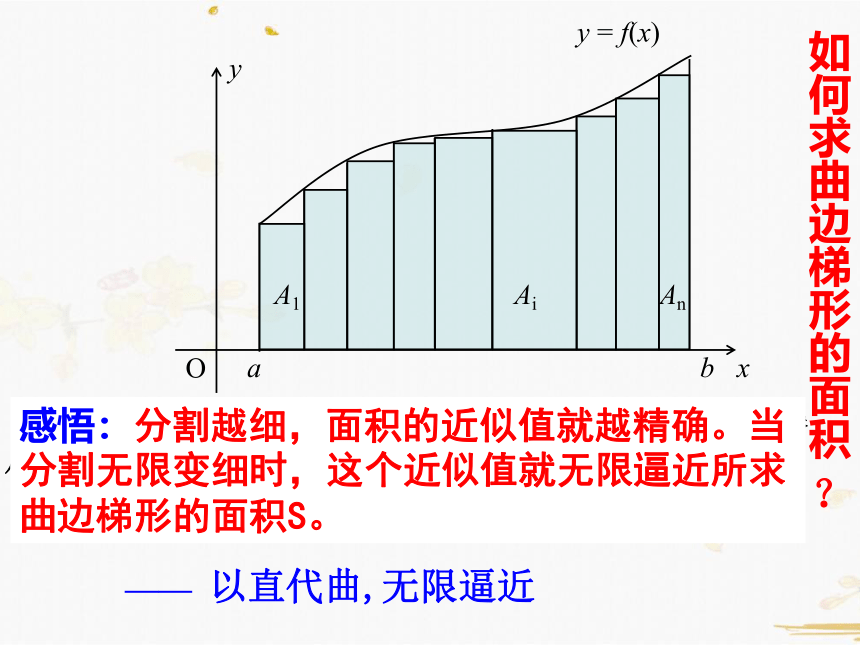
A ? A1+ A2 + ? ? ? + An
将曲边梯形分成 n个小曲边梯形,并用小矩阵形的面积代替
小曲边梯形的面积, 于是曲边梯形的面积A近似为
A1
Ai
An
—— 以直代曲,无限逼近
如何求曲边梯形的面积
?
感悟:分割越细,面积的近似值就越精确。当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S。
⑴分割
⑵近似代替
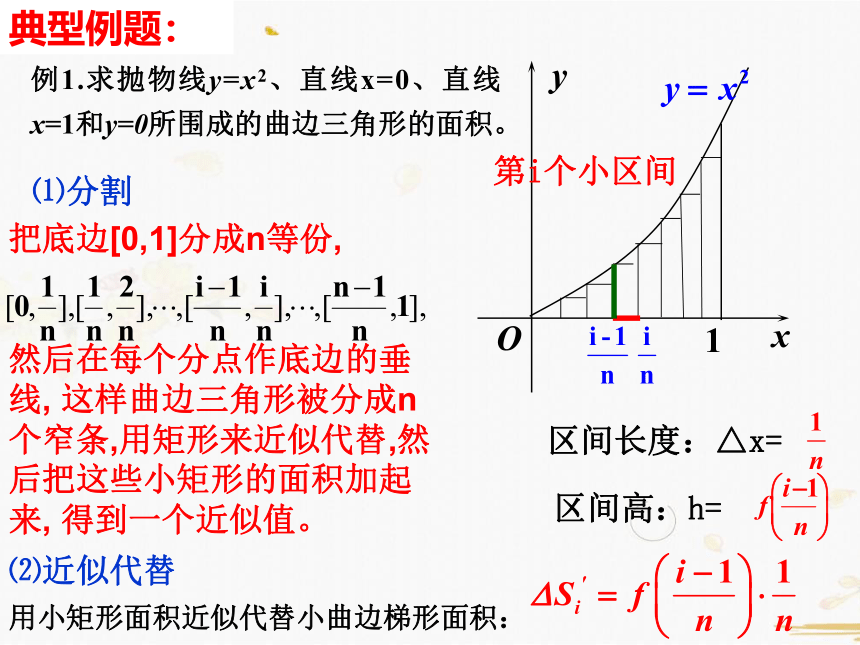
区间长度:△x=
区间高:h=
用小矩形面积近似代替小曲边梯形面积:
第i个小区间
例1.求抛物线y=x2、直线x=0、直线x=1和y=0所围成的曲边三角形的面积。
典型例题:
把底边[0,1]分成n等份,
然后在每个分点作底边的垂线, 这样曲边三角形被分成n个窄条,用矩形来近似代替,然后把这些小矩形的面积加起来, 得到一个近似值。
⑶求和
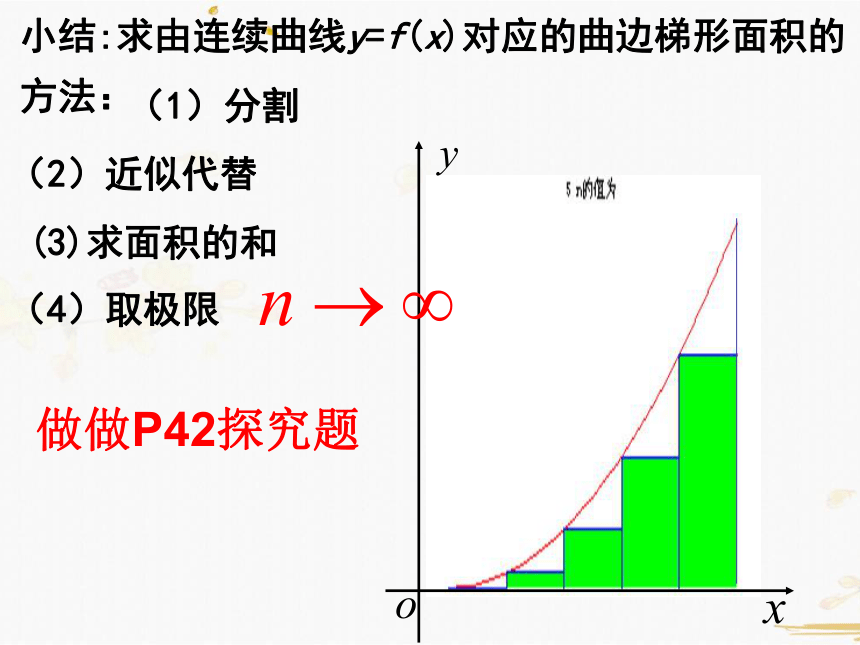
小结:求由连续曲线y=f(x)对应的曲边梯形面积的方法:
(1)分割
(2)近似代替
(3)求面积的和
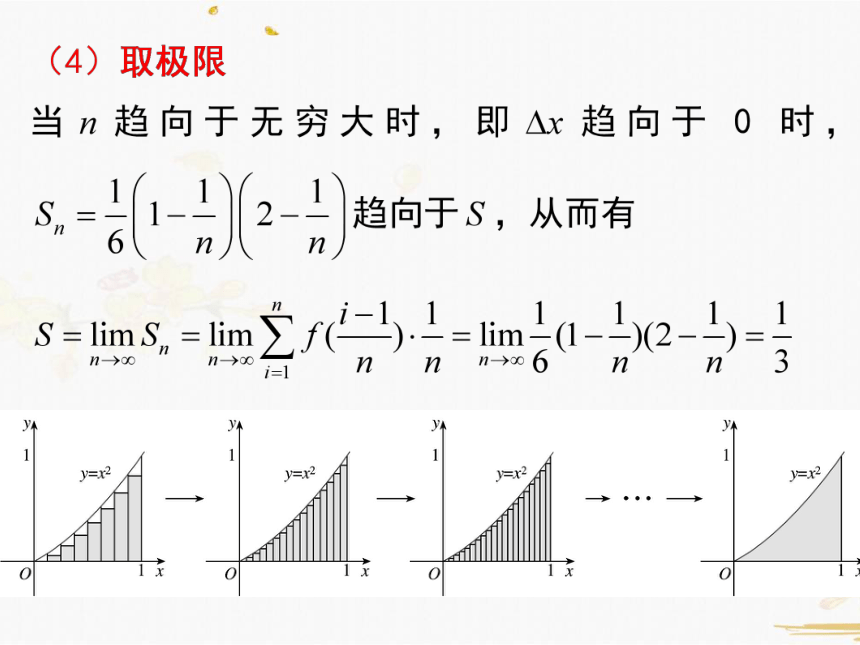
(4)取极限
做做P42探究题
练习
思考:如何求在区间[a,b]上的一般函数y=f(x)对应的曲边梯形的面积?
一、定积分的定义
如果当n?∞时,S 的无限接近某个常数,
这个常数为函数f(x)在区间[a, b]上的定积分,记作
定积分的定义:
定积分的相关名称:
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。
1
x
y
O
f(x)=x2
O
v
t
1
2
3.定积分的值与积分变量用什么字母表示无关,即有
4.规定:
是一个确定的常数
注:
2 当
的极限存在时,其极限值仅与被积函数
及积分区间
有关,而与区间
的分法及
点的取法无关。
f(x)
[a,b]
定积分的几何意义:
O
x
y
a
b
y?f (x)
x=a、x=b与 x轴所围成的曲边梯形的面积。
当f(x)?0时,由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方,
x
y
O
= -
a
b
y?f (x)
y?-f (x)
=-S
上述曲边梯形面积的负值。
定积分的几何意义:
= -S
a
b
y?f (x)
O
x
y
探究:
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?
a
b
y?f (x)
O
x
y
定积分的基本性质
性质1.
性质2.
定积分的基本性质
定积分关于积分区间具有可加性
性质3.
O
x
y
a
b
y?f (x)
C
例1:利用定积分的定义,计算
的值.
解:
做P48练习
例
x
1
y
面积值为圆的面积的
练习:
解:
x
y
f(x)=sinx
1
-1
例2.用定积分表示图中四个阴影部分面积
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
1、利用定积分的几何意义,判断下列定积分
值的正、负号。
2、利用定积分的几何意义,说明下列各式成立:
1).
2).
1).
2).
练习:
3、试用定积分表示下列各图中影阴部分的面积。
0
y
x
y=x2
1
2
0
x
y=f(x)
y=g(x)
a
b
y
直线
几条线段连成的折线
问题思考:
a
b
y = f(x)
b
a
x
y
O
A1
A ?
A1.
用一个矩形的面积A1近似代替曲边梯形的面积A,
得
如何求曲边梯形的面积
?
A ?
A1+ A2
用两个矩形的面积 近似代替曲边梯形的面积A, 得
y = f(x)
b
a
x
y
O
A1
A2
如何求曲边梯形的面积
?
A ? A1+ A2+ A3+ A4
用四个矩形的面积 近似代替曲边梯形的面积A, 得
y = f(x)
b
a
x
y
O
A1
A2
A3
A4
如何求曲边梯形的面积
?
y = f(x)
b
a
x
y
O
A ? A1+ A2 + ? ? ? + An
将曲边梯形分成 n个小曲边梯形,并用小矩阵形的面积代替
小曲边梯形的面积, 于是曲边梯形的面积A近似为
A1
Ai
An
—— 以直代曲,无限逼近
如何求曲边梯形的面积
?
感悟:分割越细,面积的近似值就越精确。当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S。
⑴分割
⑵近似代替
区间长度:△x=
区间高:h=
用小矩形面积近似代替小曲边梯形面积:
第i个小区间
例1.求抛物线y=x2、直线x=0、直线x=1和y=0所围成的曲边三角形的面积。
典型例题:
把底边[0,1]分成n等份,
然后在每个分点作底边的垂线, 这样曲边三角形被分成n个窄条,用矩形来近似代替,然后把这些小矩形的面积加起来, 得到一个近似值。
⑶求和
小结:求由连续曲线y=f(x)对应的曲边梯形面积的方法:
(1)分割
(2)近似代替
(3)求面积的和
(4)取极限
做做P42探究题
练习
思考:如何求在区间[a,b]上的一般函数y=f(x)对应的曲边梯形的面积?
一、定积分的定义
如果当n?∞时,S 的无限接近某个常数,
这个常数为函数f(x)在区间[a, b]上的定积分,记作
定积分的定义:
定积分的相关名称:
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。
1
x
y
O
f(x)=x2
O
v
t
1
2
3.定积分的值与积分变量用什么字母表示无关,即有
4.规定:
是一个确定的常数
注:
2 当
的极限存在时,其极限值仅与被积函数
及积分区间
有关,而与区间
的分法及
点的取法无关。
f(x)
[a,b]
定积分的几何意义:
O
x
y
a
b
y?f (x)
x=a、x=b与 x轴所围成的曲边梯形的面积。
当f(x)?0时,由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方,
x
y
O
= -
a
b
y?f (x)
y?-f (x)
=-S
上述曲边梯形面积的负值。
定积分的几何意义:
= -S
a
b
y?f (x)
O
x
y
探究:
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?
a
b
y?f (x)
O
x
y
定积分的基本性质
性质1.
性质2.
定积分的基本性质
定积分关于积分区间具有可加性
性质3.
O
x
y
a
b
y?f (x)
C
例1:利用定积分的定义,计算
的值.
解:
做P48练习
例
x
1
y
面积值为圆的面积的
练习:
解:
x
y
f(x)=sinx
1
-1
例2.用定积分表示图中四个阴影部分面积
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
1、利用定积分的几何意义,判断下列定积分
值的正、负号。
2、利用定积分的几何意义,说明下列各式成立:
1).
2).
1).
2).
练习:
3、试用定积分表示下列各图中影阴部分的面积。
0
y
x
y=x2
1
2
0
x
y=f(x)
y=g(x)
a
b
y
