2020-2021学年人教版八年级数学下册课件16.1.1二次根式的概念(共21张)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册课件16.1.1二次根式的概念(共21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 11:08:10 | ||
图片预览







文档简介
第十六章 二次根式
16.1.1二次根式的概念
1)了解二次根式的概念
重点:了解二次根式的概念,二次根式有意义的条件与含字母的取值范围
难点:二次根式的双重非负性
理解二次根式有意义的条件,并会求二次根式含字母的取值范围
教学目标
理解二次根式的非负性
温故而知新
(1)3的平方根是______
(2)3的算术平方根是____
(3) 有意义吗?为什么?
(4)一个非负数 的算术平方根应表示为_____
温故而知新
平方根的性质:正数有两个平方根且互为相反数;0有一个平方根就是0;负数没有平方根.
算术平方根的性质:正数和0都有算术平方根;负数没有算术平方根.
确吗?
想一想
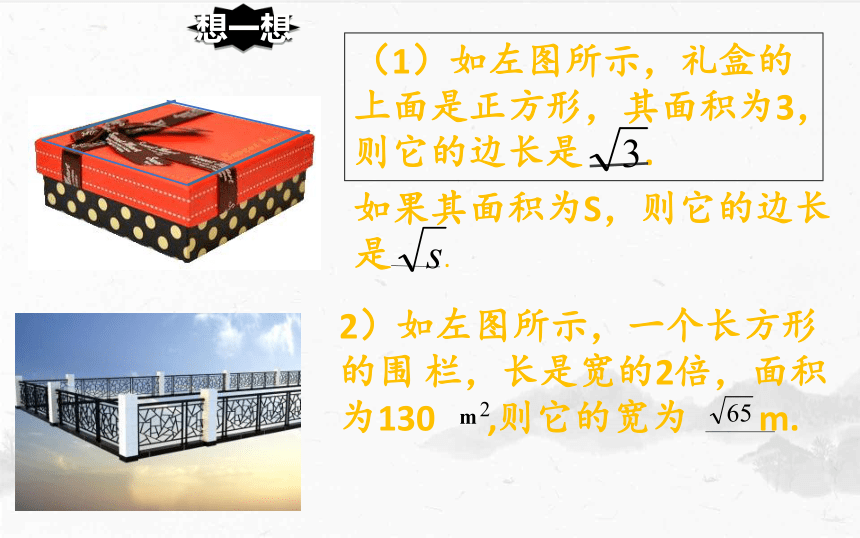
(1)如左图所示,礼盒的上面是正方形,其面积为3,则它的边长是 .
如果其面积为S,则它的边长是 .
2)如左图所示,一个长方形的围 栏,长是宽的2倍,面积为130 ,则它的宽为 m.
(3)一个物体从高处自由落下,落到地面所用的时间ts,与开始落下时离地面的高度hm。满足关系式 如果用含有h的式子表示t,那么为 .
问题1 上面问题的结果分别是
学 习 新 知
(1)这些式子分别是表示什么意义?
分别表示 的算术平方根
(2)这些式子有什么共同特征?
1.根指数都是2
2.被开方数为非负数 ,a≥0
二次根式的定义
形如 (a≥0)的式子叫做二次根式,“ ” 称为二次根式, 叫做被开方数。
3
游戏规则:5个金蛋中任选一个,如果出现金花,你不需要回答问题,直接加5分,不出现金花则判断给出的式子是不是二次根式.
2
5
1
4
探究一:砸金蛋
判断给出的式子是不是二次根式.
判断给出的式子是不是二次根式.
判断给出的式子是不是二次根式.
恭喜你,加5分
判断给出的式子是不是二次根式.
例:下列各式中,哪些是二次根式?并指出二次根式中的被开方数.
解: >0)
是二次根式.其中被开方数依次是7,x-3,(x+1)2,
【变式训练】下列各式中,一定是二次根式的是 ( )
A. B. C. D. (a<0)
〔解析〕 的被开方数-9<0, 的被开方数m-1可能是负数, 的根指数是3,所以选项A,B,C中的式子都不是二次根式. 含有二次根号,并且无论a取什么负数,被开方数a2+8都是正数,所以 一定是二次根式.故选D.
D
例:(教材例1)当x是怎样的实数时,
在实数范围内有意义?
解:由x-2≥0,得x≥2.
当x≥2时, 在实数范围内有意义.
【变式训练】若式子1+ 有意义,则x的取值范围是 .?
〔解析〕根据二次根式的性质可知:x+1≥0,即x≥-1;又因为分式的分母不能为0,所以x的取值范围是x≥-1且x≠0.故填x≥-1且x≠0.
[易错分析]容易产生只考虑到x+1≥0,
而忽略了x≠0的错误.
x≥-1且x≠0
(1)二次根式的定义是从代数式的结果和形式上界定的,必须含有二次根号“ ”,如 , 都是二次根式,而
就不是二次根式了.
(2)在二次根式中,被开方数可以是具体的数,也可以是含有字母的单项式、多项式、分式等代数式.
(3)形如b (a≥0)的式子也是二次根式,其表示的是b与的乘积,如3 表示3× .
(4)当a≥0时, 表示a的算术平方根.也就是说, 有意义的条件是a≥0.
(5)当a是非负数时, (其中a≥0)本身也是一个非负数.
必做题:1.下列各式中:① ;② ;③ ;④ ;
⑤ ,其中是二次根式的有 . (写序号)
选做题:1.已知 ,则 的值为 .
2.若式子 有意义,则P(a,b)在第 象限.
作业设计
2.代数式 有意义,则字母x的取值范围是 .
3.代数式 的值为0,则a= .
小组合作题:
1.已知m,n满足 ,求:(1)m,n的值.
(2)将m,n的值代入并化简:
(3)请选一个你喜欢的x的值代入求值.
16.1.1二次根式的概念
1)了解二次根式的概念
重点:了解二次根式的概念,二次根式有意义的条件与含字母的取值范围
难点:二次根式的双重非负性
理解二次根式有意义的条件,并会求二次根式含字母的取值范围
教学目标
理解二次根式的非负性
温故而知新
(1)3的平方根是______
(2)3的算术平方根是____
(3) 有意义吗?为什么?
(4)一个非负数 的算术平方根应表示为_____
温故而知新
平方根的性质:正数有两个平方根且互为相反数;0有一个平方根就是0;负数没有平方根.
算术平方根的性质:正数和0都有算术平方根;负数没有算术平方根.
确吗?
想一想
(1)如左图所示,礼盒的上面是正方形,其面积为3,则它的边长是 .
如果其面积为S,则它的边长是 .
2)如左图所示,一个长方形的围 栏,长是宽的2倍,面积为130 ,则它的宽为 m.
(3)一个物体从高处自由落下,落到地面所用的时间ts,与开始落下时离地面的高度hm。满足关系式 如果用含有h的式子表示t,那么为 .
问题1 上面问题的结果分别是
学 习 新 知
(1)这些式子分别是表示什么意义?
分别表示 的算术平方根
(2)这些式子有什么共同特征?
1.根指数都是2
2.被开方数为非负数 ,a≥0
二次根式的定义
形如 (a≥0)的式子叫做二次根式,“ ” 称为二次根式, 叫做被开方数。
3
游戏规则:5个金蛋中任选一个,如果出现金花,你不需要回答问题,直接加5分,不出现金花则判断给出的式子是不是二次根式.
2
5
1
4
探究一:砸金蛋
判断给出的式子是不是二次根式.
判断给出的式子是不是二次根式.
判断给出的式子是不是二次根式.
恭喜你,加5分
判断给出的式子是不是二次根式.
例:下列各式中,哪些是二次根式?并指出二次根式中的被开方数.
解: >0)
是二次根式.其中被开方数依次是7,x-3,(x+1)2,
【变式训练】下列各式中,一定是二次根式的是 ( )
A. B. C. D. (a<0)
〔解析〕 的被开方数-9<0, 的被开方数m-1可能是负数, 的根指数是3,所以选项A,B,C中的式子都不是二次根式. 含有二次根号,并且无论a取什么负数,被开方数a2+8都是正数,所以 一定是二次根式.故选D.
D
例:(教材例1)当x是怎样的实数时,
在实数范围内有意义?
解:由x-2≥0,得x≥2.
当x≥2时, 在实数范围内有意义.
【变式训练】若式子1+ 有意义,则x的取值范围是 .?
〔解析〕根据二次根式的性质可知:x+1≥0,即x≥-1;又因为分式的分母不能为0,所以x的取值范围是x≥-1且x≠0.故填x≥-1且x≠0.
[易错分析]容易产生只考虑到x+1≥0,
而忽略了x≠0的错误.
x≥-1且x≠0
(1)二次根式的定义是从代数式的结果和形式上界定的,必须含有二次根号“ ”,如 , 都是二次根式,而
就不是二次根式了.
(2)在二次根式中,被开方数可以是具体的数,也可以是含有字母的单项式、多项式、分式等代数式.
(3)形如b (a≥0)的式子也是二次根式,其表示的是b与的乘积,如3 表示3× .
(4)当a≥0时, 表示a的算术平方根.也就是说, 有意义的条件是a≥0.
(5)当a是非负数时, (其中a≥0)本身也是一个非负数.
必做题:1.下列各式中:① ;② ;③ ;④ ;
⑤ ,其中是二次根式的有 . (写序号)
选做题:1.已知 ,则 的值为 .
2.若式子 有意义,则P(a,b)在第 象限.
作业设计
2.代数式 有意义,则字母x的取值范围是 .
3.代数式 的值为0,则a= .
小组合作题:
1.已知m,n满足 ,求:(1)m,n的值.
(2)将m,n的值代入并化简:
(3)请选一个你喜欢的x的值代入求值.
