2020-2021学年北师大版七年级数学下册第四章《三角形》回顾与思考(一)课件(32张)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第四章《三角形》回顾与思考(一)课件(32张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 665.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 00:00:00 | ||
图片预览


文档简介
第四章三角形
回顾与思考(一)
三
角
形
图
形
的
全
等
丰
富
的
情
境
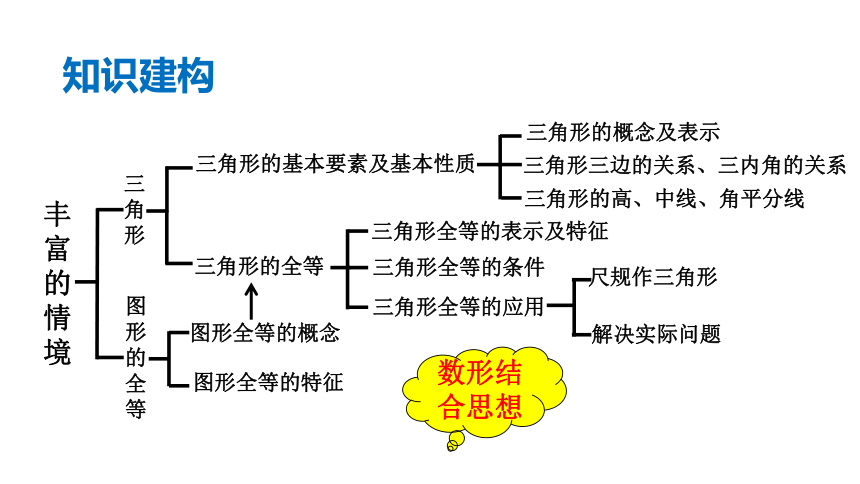
三角形三边的关系、三内角的关系
三角形的基本要素及基本性质
三角形的概念及表示
三角形的高、中线、角平分线
图形全等的概念
图形全等的特征
三角形的全等
三角形全等的表示及特征
三角形全等的条件
三角形全等的应用
解决实际问题
尺规作三角形
数形结合思想
知识建构
(一)概念及表示
1.由不在同一直线上的三条线段首尾 所组成的图形叫做三角形. 上图三角形记作 ,读作“三角形ABC ”.
2.三角形的基本元素有 、 、 .
(二)三角形三个内角的和等于 .
顺次相接
△ABC
180°
A
B
C
三条边
三个内角
三个顶点
要点梳理
一、三角形的基本要素及基本性质
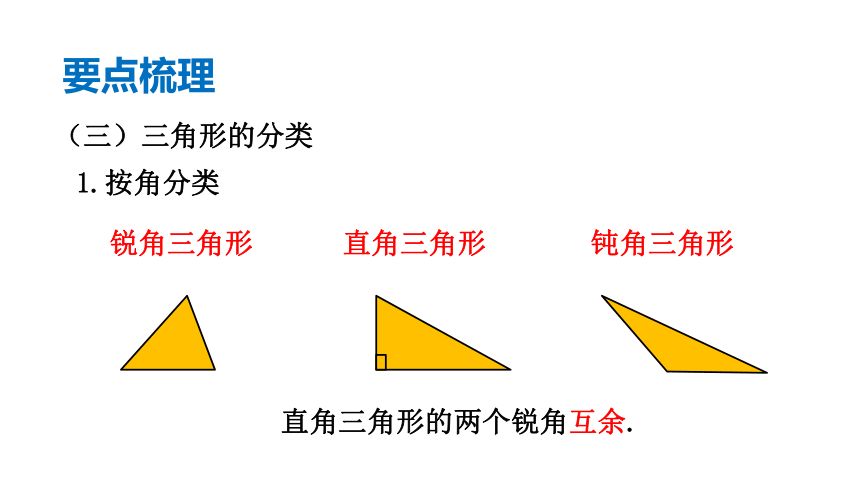
1.按角分类
(三)三角形的分类
直角三角形
钝角三角形
锐角三角形
直角三角形的两个锐角互余.
要点梳理
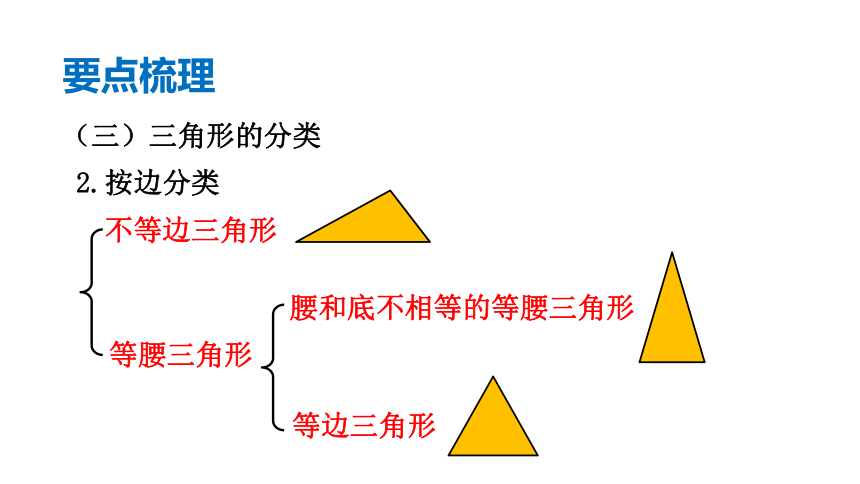
(三)三角形的分类
2.按边分类
等腰三角形
腰和底不相等的等腰三角形
等边三角形
不等边三角形
要点梳理
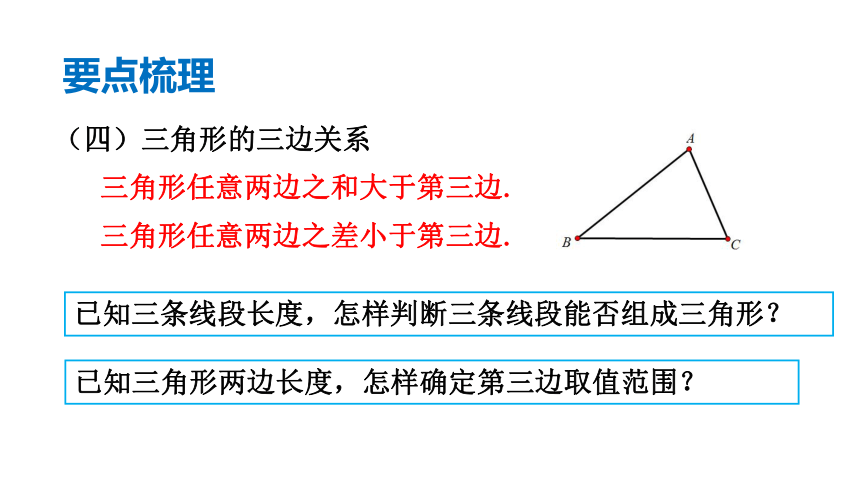
(四)三角形的三边关系
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
已知三角形两边长度,怎样确定第三边取值范围?
已知三条线段长度,怎样判断三条线段能否组成三角形?
要点梳理
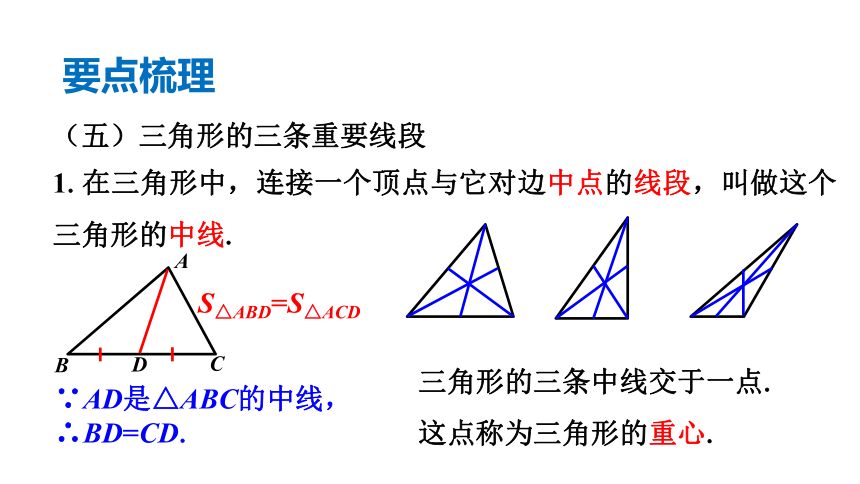
三角形的三条中线交于一点.
这点称为三角形的重心.
(五)三角形的三条重要线段
1.在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.
B
C
D
∵AD是△ABC的中线,
∴BD=CD.
S△ABD=S△ACD
要点梳理
A
B
A
C
E
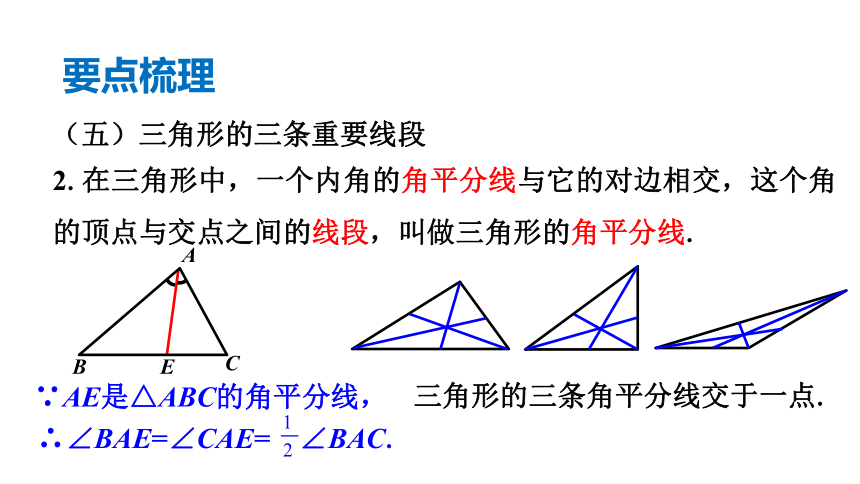
∴∠BAE=∠CAE= ∠BAC.
2.在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
三角形的三条角平分线交于一点.
要点梳理
(五)三角形的三条重要线段
∵AE是△ABC的角平分线,
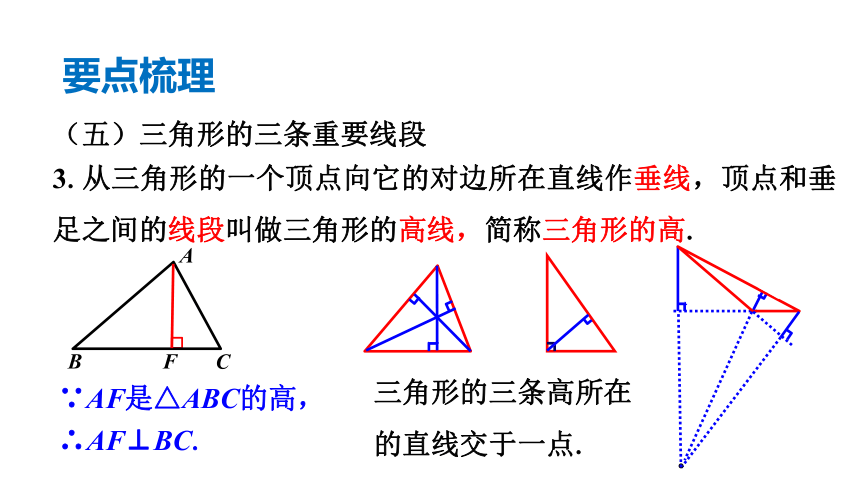
∵AF是△ABC的高,
3.从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
A
B
C
F
要点梳理
(五)三角形的三条重要线段
∴AF⊥BC.
三角形的三条高所在
的直线交于一点.
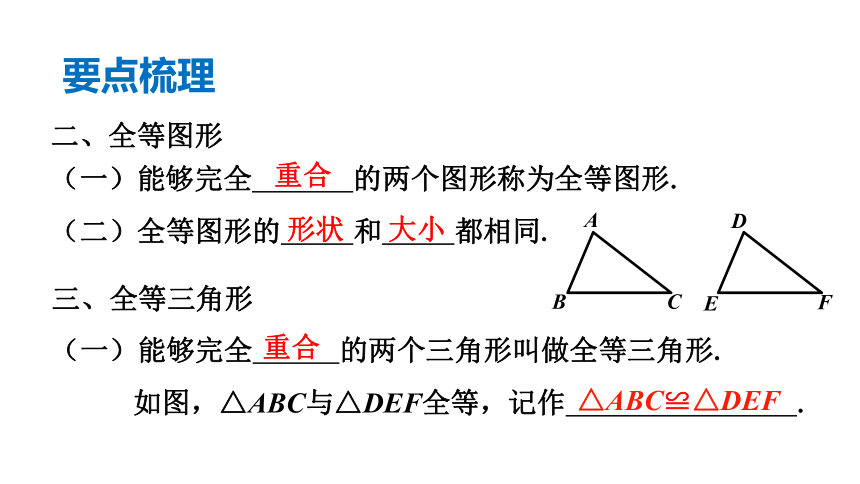
(一)能够完全 的两个图形称为全等图形.
(二)全等图形的 和 都相同.
形状
大小
二、全等图形
重合
三、全等三角形
(一)能够完全 的两个三角形叫做全等三角形.
重合
? 如图,△ABC与△DEF全等,记作 .
A
B
C
D
E
F
△ABC≌△DEF
要点梳理
A
B
C
D
E
F
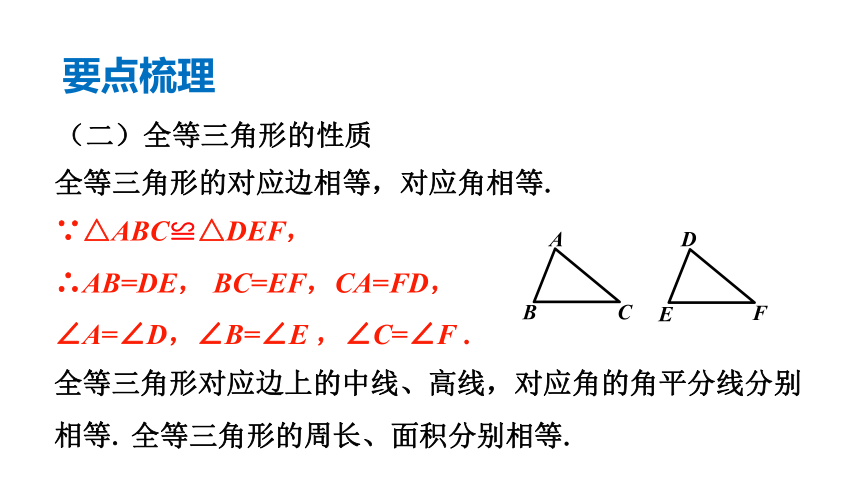
全等三角形的对应边相等,对应角相等.
(二)全等三角形的性质
∵△ABC≌△DEF,
∴AB=DE, BC=EF,CA=FD,
∠A=∠D,∠B=∠E ,∠C=∠F .
全等三角形对应边上的中线、高线,对应角的角平分线分别相等.
要点梳理
全等三角形的周长、面积分别相等.
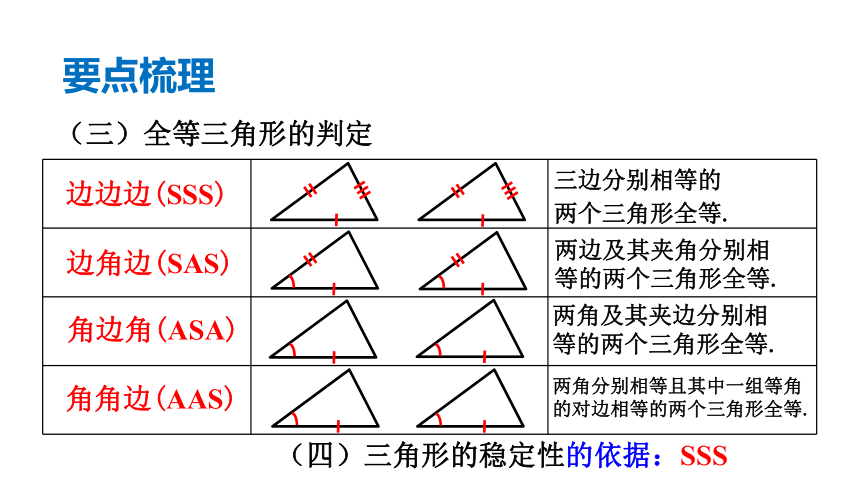
(三)全等三角形的判定
边边边(SSS)
三边分别相等的
两个三角形全等.
边角边(SAS)
两边及其夹角分别相
等的两个三角形全等.
角边角(ASA)
两角及其夹边分别相等的两个三角形全等.
(四)三角形的稳定性的依据:SSS
要点梳理
角角边(AAS)
两角分别相等且其中一组等角的对边相等的两个三角形全等.
例1:已知三角形两边长分别为3和8,第三边a的长为奇数,
问第三边应取多长?
解:由三角形任意两边之和大于第三边,任意两边之差小于第三边,得
8-3<a<8+3, 所以5<a<11.
又因为第三边的长为奇数,所以第三边长为7或9.
典例分析
考点一 三角形的三边关系、三角关系
2.△ABC中,三个内角∠A、∠B、∠C满足∠A比∠B大20o,
∠C为∠B的2倍,则∠B= °
1.已知等腰三角形两边长分别为10和4,则三角形周长是 .
24
40
设∠B=xo,则∠A=(x+20)o,∠C=2xo
(x+20)+x+2x=180
分类讨论思想
方程
思想
10、10、4
( √ )
4、4、10
(×)
针对训练一
例2:如图1,CD是∠ACB的平分线,DE∥BC,∠A=50°,
∠B=70°,求∠EDC、∠BDC的度数.
解:∵∠A+∠B +∠ACB =180°,
∴∠ACB=180°-∠A-∠B.
∵∠A=50°,∠B=70°,
∴∠ACB =180°-50°-70°=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB= ×60°=30°.
图1
典例分析
考点二 三角形的中线、角平分线、高线
数形结合思想
∵DE∥BC,
∴∠EDC=∠BCD=30°.
∵∠BCD+∠BDC+∠B=180°,
∴ ∠BDC=180°- ∠B -∠BCD
=180°-70°-30°
=80°.
3.如图2,在△ABC中,两条角平分线BD和CE相交于点O,∠BOC=116°,则∠A= °.
4.如图3,在△ABC中,CE、BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF= °,
∠FBC= °.
5.如图4,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC、△ADF和
△BEF的面积分别为S△ABC 、S△ADF和S△BEF,且S△ABC=12,则S△ADF - S△BEF = .
20
40
52
图3
图2
针对训练二
图4
5.如图4,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设
△ABC、△ADF和△BEF的面积分别为S△ABC 、S△ADF和S△BEF,且
S△ABC=12,则S△ADF - S△BEF = .
解:∵点D是AC的中点,所以AD= AC,
∵S△ABC=12,
∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE= S△ABC= ×12=4.
2
∵S△ABD - S△ABE
=(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF - S△BEF,
∴S△ADF - S△BEF
=S△ABD - S△ABE
=6-4=2.
转化
思想
图4
针对训练二
说明: ∵AE=CF,
∴AE - EF=CF - EF.
即AF=CE.
在△AFD和△CEB中,
A
D
B
C
F
E
例3:如图5,AE=CF,∠AFD=∠CEB,DF=BE.说明△AFD≌△CEB.
∴△AFD≌△CEB .
(SAS)
转化“间接条件”判全等
归纳总结:
解题思路
(1)需要得出什么结论
(2)题目已有什么条件
(3)还缺什么条件
(4)创造条件(添加辅助线)
图5
典例分析
考点三 全等三角形的判定和性质
归纳总结
A
B
C
D
找全等三角形的对应元素时一般有什么规律?
(1)有公共边的,公共边是对应边.
A
B
C
D
图6
图7
归纳总结
C
D
A
B
E
(2)有公共角的,公共角是对应角.
(3)有对顶角的,对顶角是对应角.
B
D
A
C
找全等三角形的对应元素时一般有什么规律?
图8
图9
O
找全等三角形的对应元素时一般有什么规律?
归纳总结
(4)一对最长的边是对应边,
(5)一对最大的角是对应角,
P
A
B
D
C
A
B
C
D
E
F
图10
图11
一对最短的边是对应边.
一对最小的角是对应角.
6.挖掘“隐含条件”判全等
(1)如图12,AB=DC,AC=DB,△ABC与△DCB全等吗?
A
D
B
C
图12
(2)如图13,点D在AB上,点E在AC上,CD与BE相交于点O,AD=AE,AB=AC.
若∠B=20°,CD=5cm,则∠C= ,BE= .
B
C
O
D
E
A
图13
(3)如图14,AC与BD相交于点O,OB=OD,∠A=∠C,若AB=3cm,则CD= .
图14
20°
5cm
3cm
A
D
B
C
O
△ABC≌△DCB
针对训练三
(1)平行——角相等; (2)对顶角——角相等;
(3)公共角——角相等; (4)角平分线——角相等;
(5)垂直——角相等; (6)中点——边相等;
(7)公共边——边相等;
(8)折叠、旋转——角相等,边相等.
归纳总结
解读已知条件中相等的边和角:
如图15,已知AD平分∠BAC,要使△ABD≌△ACD,可添加什么条件?
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
AB=AC
∠BDA=∠CDA
7.开放性问题:添条件判全等
A
B
C
D
归纳总结:添加条件的题目,首先要找到已具备的条件.这些条件有些是题目已知条件,有些是图中隐含条件.
∠B=∠C
分类讨论思想
图15
AS
针对训练三
找任一角
→AAS
→找任一边
说明两个三角形全等时,要认真分析条件和图形结构,理清已知与未知之间的内在联系,从而选择恰当的方法,一般的思路有:
已知两边
已知一角一边
找角的另一邻边→SAS
找夹角→SAS
边为角的对边
已知两角
→ASA
边为角的邻边
归纳总结
分类讨
论思想
数形结
合思想
找第三边→SSS
→找任一角→AAS
→AAS
→ASA
已知两边分别相等
找夹角或第三边
已知一角一边分别相等
可找任一角(当边为角的邻边时,也可找另一邻边)
已知两角分别相等
找任一边
8.已知△ABC为等腰三角形,AB=AC,点D为直线BC上一动点(点D不与点B、
点C重合).以AD为边作△ADE,且AD=AE,连接CE,∠BAC=∠DAE.
(1)如图16,当点D在边BC上时,试说明:①△ABD≌△ACE;②BC=DC+CE;
(2)如图17,当点D在边BC的延长线上时,其他条件不变,探究线段BC、DC、
CE之间存在的数量关系,并说明理由.
图16
图17
针对训练三
(1)①说明:∵∠BAC=∠DAE,
∴∠BAC -∠CAD=∠DAE - ∠CAD.
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
②说明:∵△ABD≌△ACE,
∴BD=CE.
∴BC=DC+BD=DC+CE.
图16
图17
(2)解:BC=CE - DC.
理由如下:
∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD.
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∴BC=BD - DC=CE - DC.
针对训练三
一、能运用三角形基本要素及基本性质解决问题.
二、能运用三角形全等的条件和性质解决问题.
数形结合思想
分类讨论思想
转化
思想
方程
思想
综合建模
(C层)
(B层)
(A层)
当堂检测
2.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS”为依据,需添加条件 ;
若要以“ASA”为依据,需添加条件 ;
若要以“AAS”为依据,需添加条件 .
3.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线
BD、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
1.如图,在△ABC中,∠B=63°,∠C=46°,AD和AE分别是它的高和角平分线,
则∠DAE的度数为______.
A
B
C
D
E
F
第2题图
第3题图
第1题图
当堂检测答案
1.8.5o
2.AB=DE;
∠ACB=∠F或AC∥DF;
∠A=∠D .
3.解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵BD⊥DE,
∴∠D=90°.
∴∠BAD+∠ABD=90°.
∴∠ABD=∠CAE.
∴△BDA≌△AEC(AAS).
∴DA=EC=2,AE=BD=3.
∴DE=DA+AE=5.
∵CE⊥DE,
∴∠E=90°.
∴∠D=∠E.
在△BDA和△AEC中,
(C层)
(B层)
(A层)
3.如图,等腰直角△ABC中,AB=AC,∠BAC=90°,过点B、C作过A点的直线l的垂
线,垂足分别为M、N.(1)你能找到一对全等三角形吗?并说明理由.
(2)线段BM、CN、MN之间有何关系?请说明理由.
(3)若将直线l旋转到右图的位置,其他条件不变,(2)中结论是否成立?若不成
立,线段BM、CN、MN之间有何关系?请说明理由.
2.如图,在△ABC中,AC⊥BC,AE为∠BAC的角平分线,ED⊥AB于点D,AB=7cm,
AC=3cm,求BD的长.
1.如图,AD是△ABC的高,BE是△ABC的角平分线,BE、AD相交于点F,已知
∠BAD=42°,则∠BFD的度数为______.
作业布置
第2题图
第1题图
第3题图
回顾与思考(一)
三
角
形
图
形
的
全
等
丰
富
的
情
境
三角形三边的关系、三内角的关系
三角形的基本要素及基本性质
三角形的概念及表示
三角形的高、中线、角平分线
图形全等的概念
图形全等的特征
三角形的全等
三角形全等的表示及特征
三角形全等的条件
三角形全等的应用
解决实际问题
尺规作三角形
数形结合思想
知识建构
(一)概念及表示
1.由不在同一直线上的三条线段首尾 所组成的图形叫做三角形. 上图三角形记作 ,读作“三角形ABC ”.
2.三角形的基本元素有 、 、 .
(二)三角形三个内角的和等于 .
顺次相接
△ABC
180°
A
B
C
三条边
三个内角
三个顶点
要点梳理
一、三角形的基本要素及基本性质
1.按角分类
(三)三角形的分类
直角三角形
钝角三角形
锐角三角形
直角三角形的两个锐角互余.
要点梳理
(三)三角形的分类
2.按边分类
等腰三角形
腰和底不相等的等腰三角形
等边三角形
不等边三角形
要点梳理
(四)三角形的三边关系
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
已知三角形两边长度,怎样确定第三边取值范围?
已知三条线段长度,怎样判断三条线段能否组成三角形?
要点梳理
三角形的三条中线交于一点.
这点称为三角形的重心.
(五)三角形的三条重要线段
1.在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线.
B
C
D
∵AD是△ABC的中线,
∴BD=CD.
S△ABD=S△ACD
要点梳理
A
B
A
C
E
∴∠BAE=∠CAE= ∠BAC.
2.在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
三角形的三条角平分线交于一点.
要点梳理
(五)三角形的三条重要线段
∵AE是△ABC的角平分线,
∵AF是△ABC的高,
3.从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.
A
B
C
F
要点梳理
(五)三角形的三条重要线段
∴AF⊥BC.
三角形的三条高所在
的直线交于一点.
(一)能够完全 的两个图形称为全等图形.
(二)全等图形的 和 都相同.
形状
大小
二、全等图形
重合
三、全等三角形
(一)能够完全 的两个三角形叫做全等三角形.
重合
? 如图,△ABC与△DEF全等,记作 .
A
B
C
D
E
F
△ABC≌△DEF
要点梳理
A
B
C
D
E
F
全等三角形的对应边相等,对应角相等.
(二)全等三角形的性质
∵△ABC≌△DEF,
∴AB=DE, BC=EF,CA=FD,
∠A=∠D,∠B=∠E ,∠C=∠F .
全等三角形对应边上的中线、高线,对应角的角平分线分别相等.
要点梳理
全等三角形的周长、面积分别相等.
(三)全等三角形的判定
边边边(SSS)
三边分别相等的
两个三角形全等.
边角边(SAS)
两边及其夹角分别相
等的两个三角形全等.
角边角(ASA)
两角及其夹边分别相等的两个三角形全等.
(四)三角形的稳定性的依据:SSS
要点梳理
角角边(AAS)
两角分别相等且其中一组等角的对边相等的两个三角形全等.
例1:已知三角形两边长分别为3和8,第三边a的长为奇数,
问第三边应取多长?
解:由三角形任意两边之和大于第三边,任意两边之差小于第三边,得
8-3<a<8+3, 所以5<a<11.
又因为第三边的长为奇数,所以第三边长为7或9.
典例分析
考点一 三角形的三边关系、三角关系
2.△ABC中,三个内角∠A、∠B、∠C满足∠A比∠B大20o,
∠C为∠B的2倍,则∠B= °
1.已知等腰三角形两边长分别为10和4,则三角形周长是 .
24
40
设∠B=xo,则∠A=(x+20)o,∠C=2xo
(x+20)+x+2x=180
分类讨论思想
方程
思想
10、10、4
( √ )
4、4、10
(×)
针对训练一
例2:如图1,CD是∠ACB的平分线,DE∥BC,∠A=50°,
∠B=70°,求∠EDC、∠BDC的度数.
解:∵∠A+∠B +∠ACB =180°,
∴∠ACB=180°-∠A-∠B.
∵∠A=50°,∠B=70°,
∴∠ACB =180°-50°-70°=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB= ×60°=30°.
图1
典例分析
考点二 三角形的中线、角平分线、高线
数形结合思想
∵DE∥BC,
∴∠EDC=∠BCD=30°.
∵∠BCD+∠BDC+∠B=180°,
∴ ∠BDC=180°- ∠B -∠BCD
=180°-70°-30°
=80°.
3.如图2,在△ABC中,两条角平分线BD和CE相交于点O,∠BOC=116°,则∠A= °.
4.如图3,在△ABC中,CE、BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF= °,
∠FBC= °.
5.如图4,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC、△ADF和
△BEF的面积分别为S△ABC 、S△ADF和S△BEF,且S△ABC=12,则S△ADF - S△BEF = .
20
40
52
图3
图2
针对训练二
图4
5.如图4,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设
△ABC、△ADF和△BEF的面积分别为S△ABC 、S△ADF和S△BEF,且
S△ABC=12,则S△ADF - S△BEF = .
解:∵点D是AC的中点,所以AD= AC,
∵S△ABC=12,
∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE= S△ABC= ×12=4.
2
∵S△ABD - S△ABE
=(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF - S△BEF,
∴S△ADF - S△BEF
=S△ABD - S△ABE
=6-4=2.
转化
思想
图4
针对训练二
说明: ∵AE=CF,
∴AE - EF=CF - EF.
即AF=CE.
在△AFD和△CEB中,
A
D
B
C
F
E
例3:如图5,AE=CF,∠AFD=∠CEB,DF=BE.说明△AFD≌△CEB.
∴△AFD≌△CEB .
(SAS)
转化“间接条件”判全等
归纳总结:
解题思路
(1)需要得出什么结论
(2)题目已有什么条件
(3)还缺什么条件
(4)创造条件(添加辅助线)
图5
典例分析
考点三 全等三角形的判定和性质
归纳总结
A
B
C
D
找全等三角形的对应元素时一般有什么规律?
(1)有公共边的,公共边是对应边.
A
B
C
D
图6
图7
归纳总结
C
D
A
B
E
(2)有公共角的,公共角是对应角.
(3)有对顶角的,对顶角是对应角.
B
D
A
C
找全等三角形的对应元素时一般有什么规律?
图8
图9
O
找全等三角形的对应元素时一般有什么规律?
归纳总结
(4)一对最长的边是对应边,
(5)一对最大的角是对应角,
P
A
B
D
C
A
B
C
D
E
F
图10
图11
一对最短的边是对应边.
一对最小的角是对应角.
6.挖掘“隐含条件”判全等
(1)如图12,AB=DC,AC=DB,△ABC与△DCB全等吗?
A
D
B
C
图12
(2)如图13,点D在AB上,点E在AC上,CD与BE相交于点O,AD=AE,AB=AC.
若∠B=20°,CD=5cm,则∠C= ,BE= .
B
C
O
D
E
A
图13
(3)如图14,AC与BD相交于点O,OB=OD,∠A=∠C,若AB=3cm,则CD= .
图14
20°
5cm
3cm
A
D
B
C
O
△ABC≌△DCB
针对训练三
(1)平行——角相等; (2)对顶角——角相等;
(3)公共角——角相等; (4)角平分线——角相等;
(5)垂直——角相等; (6)中点——边相等;
(7)公共边——边相等;
(8)折叠、旋转——角相等,边相等.
归纳总结
解读已知条件中相等的边和角:
如图15,已知AD平分∠BAC,要使△ABD≌△ACD,可添加什么条件?
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
AB=AC
∠BDA=∠CDA
7.开放性问题:添条件判全等
A
B
C
D
归纳总结:添加条件的题目,首先要找到已具备的条件.这些条件有些是题目已知条件,有些是图中隐含条件.
∠B=∠C
分类讨论思想
图15
AS
针对训练三
找任一角
→AAS
→找任一边
说明两个三角形全等时,要认真分析条件和图形结构,理清已知与未知之间的内在联系,从而选择恰当的方法,一般的思路有:
已知两边
已知一角一边
找角的另一邻边→SAS
找夹角→SAS
边为角的对边
已知两角
→ASA
边为角的邻边
归纳总结
分类讨
论思想
数形结
合思想
找第三边→SSS
→找任一角→AAS
→AAS
→ASA
已知两边分别相等
找夹角或第三边
已知一角一边分别相等
可找任一角(当边为角的邻边时,也可找另一邻边)
已知两角分别相等
找任一边
8.已知△ABC为等腰三角形,AB=AC,点D为直线BC上一动点(点D不与点B、
点C重合).以AD为边作△ADE,且AD=AE,连接CE,∠BAC=∠DAE.
(1)如图16,当点D在边BC上时,试说明:①△ABD≌△ACE;②BC=DC+CE;
(2)如图17,当点D在边BC的延长线上时,其他条件不变,探究线段BC、DC、
CE之间存在的数量关系,并说明理由.
图16
图17
针对训练三
(1)①说明:∵∠BAC=∠DAE,
∴∠BAC -∠CAD=∠DAE - ∠CAD.
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
②说明:∵△ABD≌△ACE,
∴BD=CE.
∴BC=DC+BD=DC+CE.
图16
图17
(2)解:BC=CE - DC.
理由如下:
∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD.
∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∴BC=BD - DC=CE - DC.
针对训练三
一、能运用三角形基本要素及基本性质解决问题.
二、能运用三角形全等的条件和性质解决问题.
数形结合思想
分类讨论思想
转化
思想
方程
思想
综合建模
(C层)
(B层)
(A层)
当堂检测
2.已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,
若要以“SAS”为依据,需添加条件 ;
若要以“ASA”为依据,需添加条件 ;
若要以“AAS”为依据,需添加条件 .
3.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线
BD、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
1.如图,在△ABC中,∠B=63°,∠C=46°,AD和AE分别是它的高和角平分线,
则∠DAE的度数为______.
A
B
C
D
E
F
第2题图
第3题图
第1题图
当堂检测答案
1.8.5o
2.AB=DE;
∠ACB=∠F或AC∥DF;
∠A=∠D .
3.解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°.
∵BD⊥DE,
∴∠D=90°.
∴∠BAD+∠ABD=90°.
∴∠ABD=∠CAE.
∴△BDA≌△AEC(AAS).
∴DA=EC=2,AE=BD=3.
∴DE=DA+AE=5.
∵CE⊥DE,
∴∠E=90°.
∴∠D=∠E.
在△BDA和△AEC中,
(C层)
(B层)
(A层)
3.如图,等腰直角△ABC中,AB=AC,∠BAC=90°,过点B、C作过A点的直线l的垂
线,垂足分别为M、N.(1)你能找到一对全等三角形吗?并说明理由.
(2)线段BM、CN、MN之间有何关系?请说明理由.
(3)若将直线l旋转到右图的位置,其他条件不变,(2)中结论是否成立?若不成
立,线段BM、CN、MN之间有何关系?请说明理由.
2.如图,在△ABC中,AC⊥BC,AE为∠BAC的角平分线,ED⊥AB于点D,AB=7cm,
AC=3cm,求BD的长.
1.如图,AD是△ABC的高,BE是△ABC的角平分线,BE、AD相交于点F,已知
∠BAD=42°,则∠BFD的度数为______.
作业布置
第2题图
第1题图
第3题图
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
