1.2直角三角形 基础训练-2020-2021学年北师大版八年级数学下册(Word版 含答案)
文档属性
| 名称 | 1.2直角三角形 基础训练-2020-2021学年北师大版八年级数学下册(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 328.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 16:50:19 | ||
图片预览



文档简介
北师版八年级下册数学第一章
三角形的证明
第2节《直角三角形》同步基础训练
选择。
1.△ABC中,∠ACB=90°,∠A=30°,CD为高,若BD=2cm,则AD等于(
)
A.2cm
B.4cm
C.6cm
D.8cm.
2.将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
A.
B.3
C.
D.
3.已知中,,为高,,则(
)
A.6
B.12
C.6或12
D.10
4.将一个有45°角的三角板的直角顶点放在一张宽为的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边沿所在的直线成30°角,如图所示,则三角板的直角边的长为(
)
A.
B.
C.
D.
5.ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定ABC为直角三角形的是(
)
A.∠A+∠B=∠C
B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2
D.a:b:c=3:4:6
6.已知的三个顶点,,,则的形状是(
).
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰直角三角形
7.一个三角形三边之比为,它的周长为60,则它的面积是(
).
A.144
B.120
C.196
D.60
8.在Rt△ABC中,斜边长BC=3,AB2+AC2+BC2的值为( )
A.18
B.9
C.6
D.无法计算
9.给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若,,是勾股数,且最大,则一定有;
④若三个整数,,是直角三角形的三边长,则,,一定是勾股数.
其中正确的是
(
)
A.①②
B.②③
C.③④
D.①④
10.如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出( )
A.2个
B.3个
C.4个
D.6个
填空。
11.在Rt△ABC中,∠C=90°,(1)若a=5,b=12,则c=_______;(2)b=8,c=17
,则=
___________
12.是的高且,,则____.
13.中,斜边BC=2,则AB2+AC2+BC2的值为_____.
14.在中,若,,,垂足为D,CD=2,则AB的长为______.
15.已知:,是钝角,,,则__________度.
三、解答。
16.证明命题:直角三角形30°角所对的边是斜边的一半,请写已知,求证,并证明.
已知: ;
求证: ;
证明过程:
17.如图所示,在中,,,AD与BE相交于点P,于点Q.
求证:(1).
(2).
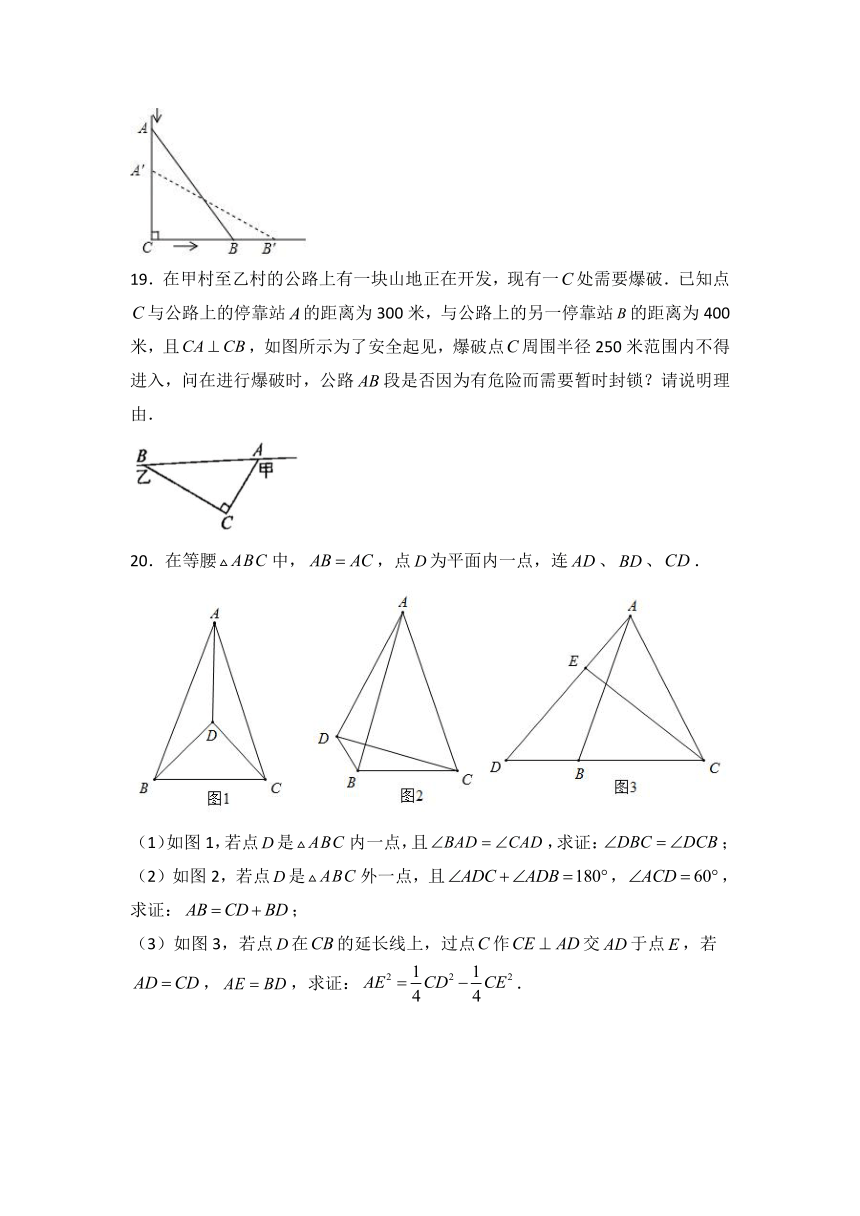
18.如图,一个长为10米的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端下滑1米,那么它的底端也滑动1米吗?试说明理由.
19.在甲村至乙村的公路上有一块山地正在开发,现有一处需要爆破.已知点与公路上的停靠站的距离为300米,与公路上的另一停靠站的距离为400米,且,如图所示为了安全起见,爆破点周围半径250米范围内不得进入,问在进行爆破时,公路段是否因为有危险而需要暂时封锁?请说明理由.
20.在等腰中,,点为平面内一点,连、、.
(1)如图1,若点是内一点,且,求证:;
(2)如图2,若点是外一点,且,,求证:;
(3)如图3,若点在的延长线上,过点作交于点,若,,求证:.
答案
1-5:CDCBD
6-10:CBACD
11.13
60
12.
13.8
14.
15.30
16.△ABC中,∠C=90°,∠A=30°;BC=AB,
证明:
延长BC到D,使CD=BC,连接AD,
∵∠ACB=90°,
∴AC⊥BD,
∴AD=AB,
∵∠ACB=90°,∠C=30°,
∴∠B=60°,
∴△ADB是等边三角形,
∴BD=AB,
∵BC=CD=BD,
∴BC=AB.
17.(1),
是等边三角形.
.
,
.
(2),
,
.
.
,
.
.
18.不是,底端B滑动距离为米
19.公路段需要暂时封锁.理由如下:
如图,过点作于点.
因为米,米,,
所以由勾股定理知,即米.
因为,
所以(米).
由于240米<250米,故有危险,因此公路段需要暂时封锁.
20.(1)证明:如图1,延长AD交BC于点G,
AB=AC,
(2)证明:如图2,延长CD至点H,使DH=BD,连接AH,
在和中
为等边三角形
又
(3)证明:如图3,延长EA至点F,使AF=AE,连接CF,
,
在和中
在中,
即
三角形的证明
第2节《直角三角形》同步基础训练
选择。
1.△ABC中,∠ACB=90°,∠A=30°,CD为高,若BD=2cm,则AD等于(
)
A.2cm
B.4cm
C.6cm
D.8cm.
2.将等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′,若AC=1,则图中阴影部分面积为( )
A.
B.3
C.
D.
3.已知中,,为高,,则(
)
A.6
B.12
C.6或12
D.10
4.将一个有45°角的三角板的直角顶点放在一张宽为的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边沿所在的直线成30°角,如图所示,则三角板的直角边的长为(
)
A.
B.
C.
D.
5.ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定ABC为直角三角形的是(
)
A.∠A+∠B=∠C
B.∠A:∠B:∠C=1:2:3
C.a2=c2﹣b2
D.a:b:c=3:4:6
6.已知的三个顶点,,,则的形状是(
).
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰直角三角形
7.一个三角形三边之比为,它的周长为60,则它的面积是(
).
A.144
B.120
C.196
D.60
8.在Rt△ABC中,斜边长BC=3,AB2+AC2+BC2的值为( )
A.18
B.9
C.6
D.无法计算
9.给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若,,是勾股数,且最大,则一定有;
④若三个整数,,是直角三角形的三边长,则,,一定是勾股数.
其中正确的是
(
)
A.①②
B.②③
C.③④
D.①④
10.如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出( )
A.2个
B.3个
C.4个
D.6个
填空。
11.在Rt△ABC中,∠C=90°,(1)若a=5,b=12,则c=_______;(2)b=8,c=17
,则=
___________
12.是的高且,,则____.
13.中,斜边BC=2,则AB2+AC2+BC2的值为_____.
14.在中,若,,,垂足为D,CD=2,则AB的长为______.
15.已知:,是钝角,,,则__________度.
三、解答。
16.证明命题:直角三角形30°角所对的边是斜边的一半,请写已知,求证,并证明.
已知: ;
求证: ;
证明过程:
17.如图所示,在中,,,AD与BE相交于点P,于点Q.
求证:(1).
(2).
18.如图,一个长为10米的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端下滑1米,那么它的底端也滑动1米吗?试说明理由.
19.在甲村至乙村的公路上有一块山地正在开发,现有一处需要爆破.已知点与公路上的停靠站的距离为300米,与公路上的另一停靠站的距离为400米,且,如图所示为了安全起见,爆破点周围半径250米范围内不得进入,问在进行爆破时,公路段是否因为有危险而需要暂时封锁?请说明理由.
20.在等腰中,,点为平面内一点,连、、.
(1)如图1,若点是内一点,且,求证:;
(2)如图2,若点是外一点,且,,求证:;
(3)如图3,若点在的延长线上,过点作交于点,若,,求证:.
答案
1-5:CDCBD
6-10:CBACD
11.13
60
12.
13.8
14.
15.30
16.△ABC中,∠C=90°,∠A=30°;BC=AB,
证明:
延长BC到D,使CD=BC,连接AD,
∵∠ACB=90°,
∴AC⊥BD,
∴AD=AB,
∵∠ACB=90°,∠C=30°,
∴∠B=60°,
∴△ADB是等边三角形,
∴BD=AB,
∵BC=CD=BD,
∴BC=AB.
17.(1),
是等边三角形.
.
,
.
(2),
,
.
.
,
.
.
18.不是,底端B滑动距离为米
19.公路段需要暂时封锁.理由如下:
如图,过点作于点.
因为米,米,,
所以由勾股定理知,即米.
因为,
所以(米).
由于240米<250米,故有危险,因此公路段需要暂时封锁.
20.(1)证明:如图1,延长AD交BC于点G,
AB=AC,
(2)证明:如图2,延长CD至点H,使DH=BD,连接AH,
在和中
为等边三角形
又
(3)证明:如图3,延长EA至点F,使AF=AE,连接CF,
,
在和中
在中,
即
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
