2020-2021学年人教版八年级数学下册专题复习16.4二次根式单元复习提升训练(Word版,附答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册专题复习16.4二次根式单元复习提升训练(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 314.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 20:04:15 | ||
图片预览


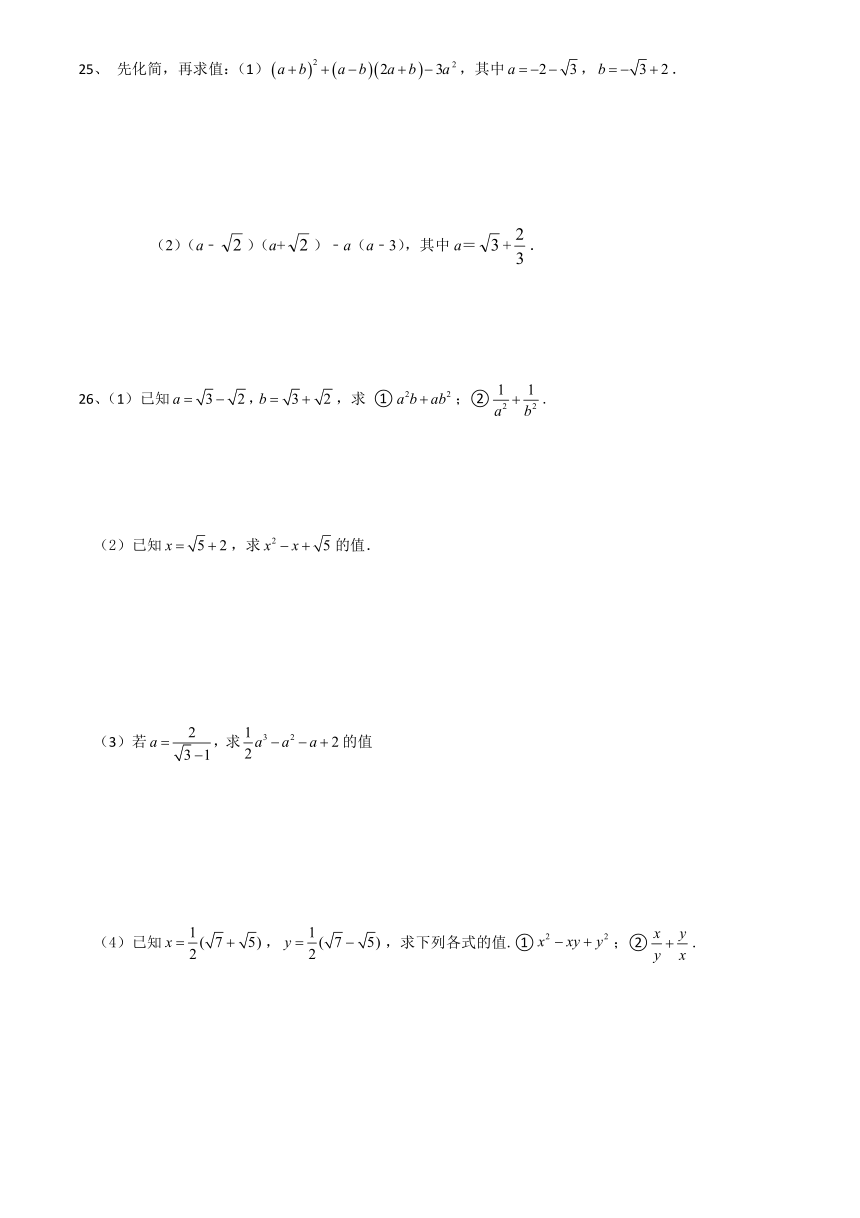
文档简介
专题复习提升训练卷16.4《二次根式》单元训练(1)-20-21人教版八年级数学下册
一、选择题
1、下列根式中,与3是同类二次根式的是
(
)
A.
B.
C.
D.
2、下列根式:中,最简二次根式的个数是
(
)
A.2个
B.3个
C.4个
D.5个
3、若,则的取值范围是
(
)
A.一4≤≤4
B.>一4
C.≤4
D.一4<<4
4、下列运算正确的是(
)
A.
B.
C.
D.
5、化简的结果是
(
)
A.
B.
C.
D.
6、计算(
)
A.7
B.-5
C.5
D.-7
7、实数在数轴上的位置如图,则
化简后为
(
)
A.7
B.一7
C.
D.无法确定
8、已知实数a,b在数轴上的位置如图所示,化简|a﹣1|+为( )
A.b﹣a
B.a﹣b
C.a+b﹣2
D.2﹣a﹣b
9、已知,若是整数,则的值可能是(
)
A.
B.
C.
D.
10、已知:a+b=﹣5,ab=1,则的值为( )
A.5
B.﹣5
C.25
D.5或﹣5
11、化简且、均不为0),
甲的解法:;
乙的解法:.下列判断中,正确的是(
)
A.甲的解法正确,乙的解法不正确
B.甲的解法不正确,乙的解法正确
C.甲、乙的解法都正确
D.甲、乙的解法都不正确
12、在数学课上,老师将一长方形纸片的长增加,宽增加,就成为了一个面积为192cm2的正方形,则原长方形纸片的面积为( )
A.18cm2
B.20cm2
C.36cm2
D.48cm2
二、填空题
13、若式子有意义,则的取值范围是
14、填空.(1)=
.(2)=
.
15、计算:=_________
16、如果,那么m的值是
.
17、当a=
时,最简二次根式与可以合并.
18、已知1<x<2,=7,则的值是_____.
19、一个长方形的长和面积分别是和,则这个长方形的宽为
.
20、若a>a+1,化简=
.
21、已知:x=,y=.那么=
.
22、观察下列各式:,…请你将猜想到的规律用含有自然数(≥1)的式子表示出来:
三、解答题
23、先阅读,后回答问题:x为何值时,有意义?
解:要使该二次根式有意义,需x(x-3)0,
由乘法法则得或,
解得x或,
即当x或有意义.
体会解题思想后,解答:x为何值时,有意义?
24、计算:
(1)
(2)
(3)
(4)
(5)
(6)
25、
先化简,再求值:(1),其中,.
(2)(a﹣)(a+)﹣a(a﹣3),其中a=+.
26、(1)已知,求
①;②.
(2)已知,求的值.
(3)若求的值
(4)已知,,求下列各式的值.①;②.
专题复习提升训练卷16.4《二次根式》单元训练(1)-20-21人教版八年级数学下册(答案)
一、选择题
1、下列根式中,与3是同类二次根式的是
(
B
)
A.
B.
C.
D.
2、下列根式:中,最简二次根式的个数是
(
A
)
A.2个
B.3个
C.4个
D.5个
3、若,则的取值范围是
(
A
)
A.一4≤≤4
B.>一4
C.≤4
D.一4<<4
4、下列运算正确的是(
D
)
A.
B.
C.
D.
5、化简的结果是
(
C
)
A.
B.
C.
D.
6、计算(
C
)
A.7
B.-5
C.5
D.-7
7、实数在数轴上的位置如图,则
化简后为
(
A
)
A.7
B.一7
C.
D.无法确定
8、已知实数a,b在数轴上的位置如图所示,化简|a﹣1|+为( )
A.b﹣a
B.a﹣b
C.a+b﹣2
D.2﹣a﹣b
解:由题可得,a﹣1<0,b﹣1>0,
∴|a﹣1|+=﹣a+1+b﹣1=﹣a+b,
故选A.
9、已知,若是整数,则的值可能是(
C
)
A.
B.
C.
D.
10、已知:a+b=﹣5,ab=1,则的值为( )
A.5
B.﹣5
C.25
D.5或﹣5
解:∵a+b=﹣5,ab=1,
∴a<0,b<0,
+=﹣﹣=﹣,
又∵a+b=﹣5,ab=1,
∴原式=﹣=5;
故选:A.
11、化简且、均不为0),
甲的解法:;
乙的解法:.下列判断中,正确的是(
C
)
A.甲的解法正确,乙的解法不正确
B.甲的解法不正确,乙的解法正确
C.甲、乙的解法都正确
D.甲、乙的解法都不正确
12、在数学课上,老师将一长方形纸片的长增加,宽增加,就成为了一个面积为192cm2的正方形,则原长方形纸片的面积为( )
A.18cm2
B.20cm2
C.36cm2
D.48cm2
解:∵一个面积为192cm2的正方形纸片,边长为:8cm,
∴原矩形的长为:8﹣2=6(cm),宽为:8﹣7=(cm),
∴则原长方形纸片的面积为:(cm2).
故选:A.
二、填空题
13、若式子有意义,则的取值范围是
且
14、填空.(1)=
.(2)=
.
解:(1);
(2);
答案为:(1)2;(2).
15、计算:=_________
解答:原式;
16、如果,那么m的值是
.
解:∵()2=3,∴m=3,答案为:3.
17、当a=
时,最简二次根式与可以合并.
解:∵最简二次根式与可以合并,∴a+2=5﹣2a,解得a=1.答案为:1.
18、已知1<x<2,=7,则的值是___-2__.
19、一个长方形的长和面积分别是和,则这个长方形的宽为
.
解:由题意知:长方形的宽为:===2,答案为:2.
20、若a>a+1,化简=
.
解:∵a>a+1,
∴(1﹣)a>1,
则a<,即a<﹣1﹣,
∴a+<﹣1,a++1<0,
原式=﹣a﹣+a++1=1,
故答案为:1.
21、已知:x=,y=.那么=
.
解:∵x==5﹣2,y==5+2,
∴原式===98,
故答案为:98
22、观察下列各式:,…请你将猜想到的规律用含有自然数(≥1)的式子表示出来:
三、解答题
23、先阅读,后回答问题:x为何值时,有意义?
解:要使该二次根式有意义,需x(x-3)0,
由乘法法则得或,
解得x或,
即当x或有意义.
体会解题思想后,解答:x为何值时,有意义?
答案:x或.
24、计算:
(1)
(2)
(3)
(4)
(5)
(6)
解:(1)原式==2-3+4=-1+4
(2)原式=3-2+=
(3)
(4)
(5)
(6)
25、
先化简,再求值:(1),其中,.
(2)(a﹣)(a+)﹣a(a﹣3),其中a=+.
解答:(1).
当,时,
(2)原式=a2﹣2﹣a2+3a=3a﹣2,
当a=+时,原式=3(+)﹣2
=3.
原式
26、(1)已知,求
①;②.
(2)已知,求的值.
(3)若求的值
(4)已知,,求下列各式的值.①;②.
解答:(1)由题意得
①原式
②原式
(2)当时,
原式
.
(3)由得即两边平方,得
∴原式=
(4)∵,,∴,.
①.
②.
一、选择题
1、下列根式中,与3是同类二次根式的是
(
)
A.
B.
C.
D.
2、下列根式:中,最简二次根式的个数是
(
)
A.2个
B.3个
C.4个
D.5个
3、若,则的取值范围是
(
)
A.一4≤≤4
B.>一4
C.≤4
D.一4<<4
4、下列运算正确的是(
)
A.
B.
C.
D.
5、化简的结果是
(
)
A.
B.
C.
D.
6、计算(
)
A.7
B.-5
C.5
D.-7
7、实数在数轴上的位置如图,则
化简后为
(
)
A.7
B.一7
C.
D.无法确定
8、已知实数a,b在数轴上的位置如图所示,化简|a﹣1|+为( )
A.b﹣a
B.a﹣b
C.a+b﹣2
D.2﹣a﹣b
9、已知,若是整数,则的值可能是(
)
A.
B.
C.
D.
10、已知:a+b=﹣5,ab=1,则的值为( )
A.5
B.﹣5
C.25
D.5或﹣5
11、化简且、均不为0),
甲的解法:;
乙的解法:.下列判断中,正确的是(
)
A.甲的解法正确,乙的解法不正确
B.甲的解法不正确,乙的解法正确
C.甲、乙的解法都正确
D.甲、乙的解法都不正确
12、在数学课上,老师将一长方形纸片的长增加,宽增加,就成为了一个面积为192cm2的正方形,则原长方形纸片的面积为( )
A.18cm2
B.20cm2
C.36cm2
D.48cm2
二、填空题
13、若式子有意义,则的取值范围是
14、填空.(1)=
.(2)=
.
15、计算:=_________
16、如果,那么m的值是
.
17、当a=
时,最简二次根式与可以合并.
18、已知1<x<2,=7,则的值是_____.
19、一个长方形的长和面积分别是和,则这个长方形的宽为
.
20、若a>a+1,化简=
.
21、已知:x=,y=.那么=
.
22、观察下列各式:,…请你将猜想到的规律用含有自然数(≥1)的式子表示出来:
三、解答题
23、先阅读,后回答问题:x为何值时,有意义?
解:要使该二次根式有意义,需x(x-3)0,
由乘法法则得或,
解得x或,
即当x或有意义.
体会解题思想后,解答:x为何值时,有意义?
24、计算:
(1)
(2)
(3)
(4)
(5)
(6)
25、
先化简,再求值:(1),其中,.
(2)(a﹣)(a+)﹣a(a﹣3),其中a=+.
26、(1)已知,求
①;②.
(2)已知,求的值.
(3)若求的值
(4)已知,,求下列各式的值.①;②.
专题复习提升训练卷16.4《二次根式》单元训练(1)-20-21人教版八年级数学下册(答案)
一、选择题
1、下列根式中,与3是同类二次根式的是
(
B
)
A.
B.
C.
D.
2、下列根式:中,最简二次根式的个数是
(
A
)
A.2个
B.3个
C.4个
D.5个
3、若,则的取值范围是
(
A
)
A.一4≤≤4
B.>一4
C.≤4
D.一4<<4
4、下列运算正确的是(
D
)
A.
B.
C.
D.
5、化简的结果是
(
C
)
A.
B.
C.
D.
6、计算(
C
)
A.7
B.-5
C.5
D.-7
7、实数在数轴上的位置如图,则
化简后为
(
A
)
A.7
B.一7
C.
D.无法确定
8、已知实数a,b在数轴上的位置如图所示,化简|a﹣1|+为( )
A.b﹣a
B.a﹣b
C.a+b﹣2
D.2﹣a﹣b
解:由题可得,a﹣1<0,b﹣1>0,
∴|a﹣1|+=﹣a+1+b﹣1=﹣a+b,
故选A.
9、已知,若是整数,则的值可能是(
C
)
A.
B.
C.
D.
10、已知:a+b=﹣5,ab=1,则的值为( )
A.5
B.﹣5
C.25
D.5或﹣5
解:∵a+b=﹣5,ab=1,
∴a<0,b<0,
+=﹣﹣=﹣,
又∵a+b=﹣5,ab=1,
∴原式=﹣=5;
故选:A.
11、化简且、均不为0),
甲的解法:;
乙的解法:.下列判断中,正确的是(
C
)
A.甲的解法正确,乙的解法不正确
B.甲的解法不正确,乙的解法正确
C.甲、乙的解法都正确
D.甲、乙的解法都不正确
12、在数学课上,老师将一长方形纸片的长增加,宽增加,就成为了一个面积为192cm2的正方形,则原长方形纸片的面积为( )
A.18cm2
B.20cm2
C.36cm2
D.48cm2
解:∵一个面积为192cm2的正方形纸片,边长为:8cm,
∴原矩形的长为:8﹣2=6(cm),宽为:8﹣7=(cm),
∴则原长方形纸片的面积为:(cm2).
故选:A.
二、填空题
13、若式子有意义,则的取值范围是
且
14、填空.(1)=
.(2)=
.
解:(1);
(2);
答案为:(1)2;(2).
15、计算:=_________
解答:原式;
16、如果,那么m的值是
.
解:∵()2=3,∴m=3,答案为:3.
17、当a=
时,最简二次根式与可以合并.
解:∵最简二次根式与可以合并,∴a+2=5﹣2a,解得a=1.答案为:1.
18、已知1<x<2,=7,则的值是___-2__.
19、一个长方形的长和面积分别是和,则这个长方形的宽为
.
解:由题意知:长方形的宽为:===2,答案为:2.
20、若a>a+1,化简=
.
解:∵a>a+1,
∴(1﹣)a>1,
则a<,即a<﹣1﹣,
∴a+<﹣1,a++1<0,
原式=﹣a﹣+a++1=1,
故答案为:1.
21、已知:x=,y=.那么=
.
解:∵x==5﹣2,y==5+2,
∴原式===98,
故答案为:98
22、观察下列各式:,…请你将猜想到的规律用含有自然数(≥1)的式子表示出来:
三、解答题
23、先阅读,后回答问题:x为何值时,有意义?
解:要使该二次根式有意义,需x(x-3)0,
由乘法法则得或,
解得x或,
即当x或有意义.
体会解题思想后,解答:x为何值时,有意义?
答案:x或.
24、计算:
(1)
(2)
(3)
(4)
(5)
(6)
解:(1)原式==2-3+4=-1+4
(2)原式=3-2+=
(3)
(4)
(5)
(6)
25、
先化简,再求值:(1),其中,.
(2)(a﹣)(a+)﹣a(a﹣3),其中a=+.
解答:(1).
当,时,
(2)原式=a2﹣2﹣a2+3a=3a﹣2,
当a=+时,原式=3(+)﹣2
=3.
原式
26、(1)已知,求
①;②.
(2)已知,求的值.
(3)若求的值
(4)已知,,求下列各式的值.①;②.
解答:(1)由题意得
①原式
②原式
(2)当时,
原式
.
(3)由得即两边平方,得
∴原式=
(4)∵,,∴,.
①.
②.
