2020-2021学年苏科版七年级数学下册7.2节探索平行线的性质同步练习(Word版,附答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册7.2节探索平行线的性质同步练习(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 234.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-25 00:00:00 | ||
图片预览



文档简介
苏科版初中数学七年级下册第七章平面图形的认识(二)7.2节探索平行线的性质同步练习
一、单选题
1.一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为(??
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?55°???????????????????????????????????????D.?60°
2.如图,已知直线l1∥l2
,
将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于(??
)
A.?39°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?51°
3.如图所示,一辆汽车经过一段公路两次拐弯后,和原来的行驶方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于142°,第二次拐的角∠C的度数为
(???
)
A.?38°?????????????????????????????????????B.?142°?????????????????????????????????????C.?130°?????????????????????????????????????D.?140°
4.下列四个图中,
一定成立的是(?????
)
A.????????????????????B.????????????????????C.????????????????????D.?
5.如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为(???
)
A.?55°??????????????????????????????????????B.?50°??????????????????????????????????????C.?45”??????????????????????????????????????D.?40°
6.如图,直线
,折线
交
于M,交
于N,点F在
与
之间,设
,
,则
的度数是
?????
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
7.如图,直线
∥
,将一块含
角的直角三角尺按图中方式放置,其中点A和点B两点分别落在直线a和b???
上.若
,则
的度数为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
8.如图,
中,∠ACB=90°,DE
过点C
,
且DE∥AB,若∠ACD=65°,则∠B的度数是(???
)
A.?25°???????????????????????????????????????B.?35°???????????????????????????????????????C.?45°???????????????????????????????????????D.?55°
9.已知a,b,c是三条直线,下列结论正确的是(???
)
A.?若a∥b,b∥c,则a∥c?????????????????????????????????????????B.?若a⊥b,b⊥c,则a⊥c
C.?若a∥b,b⊥c,则a∥c????????????????????????????????????????D.?若a⊥b,b∥c,则a∥c
10.如图所示,∠A0B
=
40°,OC平分∠AOB,直尺与OC垂直,则∠1等于(??
)
A.?60°???????????????????????????????????????B.?70°???????????????????????????????????????C.?50°???????????????????????????????????????D.?40°
11.如图,
,
,则
,
,
之间的关系是(???
)
A.?
B.?
C.?
D.?
12.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是(??
)
A.?①②③??????????????????????????B.?①②④??????????????????????????C.?①③④??????????????????????????D.?①②③④???????
图4
二、填空题
13.如图,∠1=∠2,∠A=70°,则∠ADC=________度;
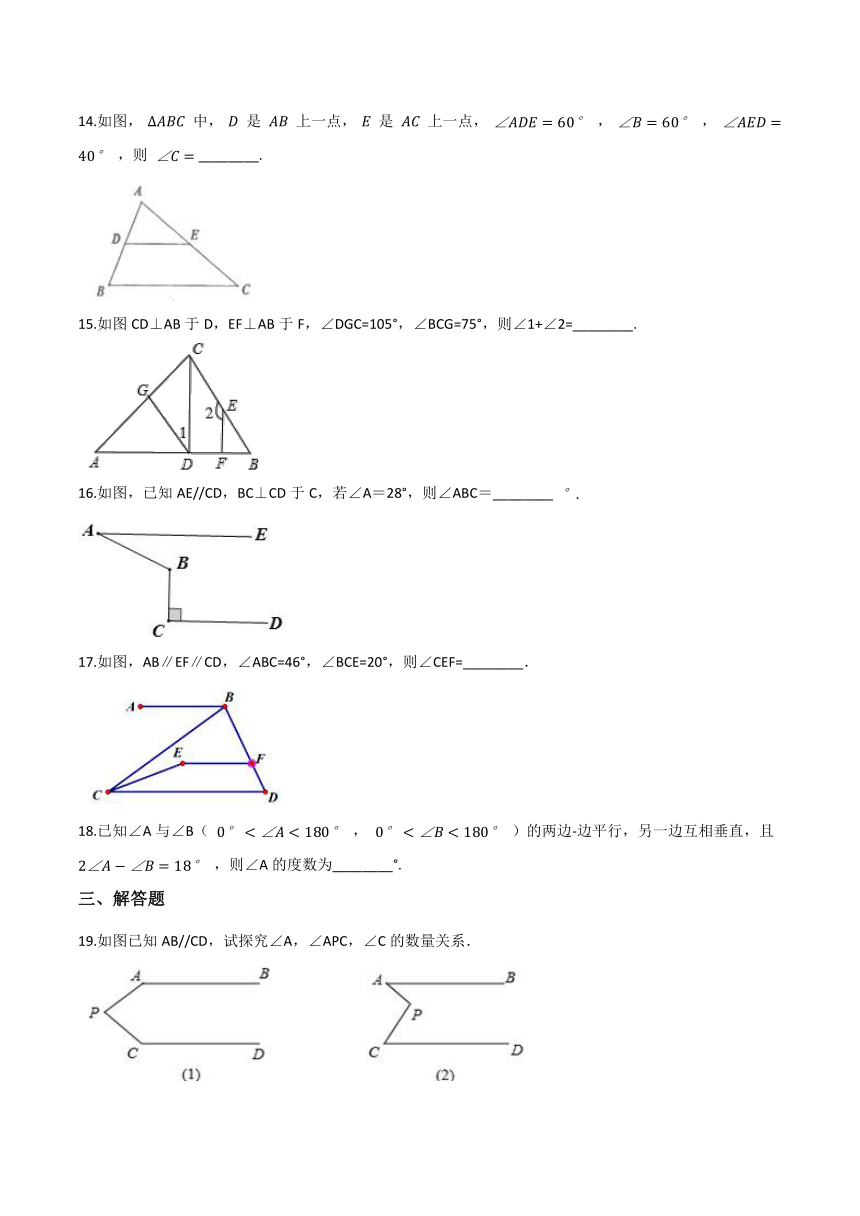
14.如图,
中,
是
上一点,
是
上一点,
,
,
,则
________.
15.如图CD⊥AB于D,EF⊥AB于F,∠DGC=105°,∠BCG=75°,则∠1+∠2=________.
16.如图,已知AE//CD,BC⊥CD于C,若∠A=28°,则∠ABC=________
17.如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=________.
?
18.已知∠A与∠B(
,
)的两边-边平行,另一边互相垂直,且
,则∠A的度数为________°.
三、解答题
19.如图已知AB//CD,试探究∠A,∠APC,∠C的数量关系.
?
20.如图,已知AB∥CD,CD∥EF,
∠A=105°,
∠ACE=51°.求
∠E.
21.如图,已知AB∥CD∥EF,PS
⊥
GH交GH于P.在
∠FRG=110°时,求
∠PSQ.
22.如图,已知直线l1∥l2
,
l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
?
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系
参考答案
1.
B
2.
D
3.
B
4.
B
5.
A
6.
D
7.
A
8.
A
9.
A
10.
B
11.
C
12.
D
13.
110
14.
40
15.
180°
16.
118
17.
154°
18.
36或96
19.
解:(1)作
,如图所示,
,
,
∴
,
∴
.
;(2)延长CP交AB于点N,
,
,
∴
,
∴
,
∴
.
20.解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=105°,
∴∠ACD=75°,
又∵∠ACE=51°,
∴∠DCE=∠ACD-∠ACE=75°-51°=24°,
∵CD∥EF,
∠E=∠DCE=24°.
21.解:∵AB∥EF,
∴∠FRG=∠APR,
∵∠FRG=110°,
∴∠APR=110°,
又∵PS⊥GH,
∴∠SPR=90°,
∴∠APS=∠APR-∠SPR=20°,
∵AB∥CD,
∴∠PSQ=∠APS=20°.
22.
(1)证明:过P作PQ∥l1∥l2
,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)解:
∠3=∠2﹣∠1;
证明:过P作直线PQ∥l1∥l2
,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
?
(3)解:
∠3=360°﹣∠1﹣∠2.
证明:过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
(4)解:
过P作PQ∥l1∥l2;
①当P在C点上方时,
同(2)可证:∠3=∠DFP﹣∠CEP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠DFP﹣∠CEP+∠2﹣∠1=0,
即∠3=∠1﹣∠2.
②当P在D点下方时,
∠3=∠2﹣∠1,解法同上.
综上可知:当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.
?
一、单选题
1.一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为(??
)
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?55°???????????????????????????????????????D.?60°
2.如图,已知直线l1∥l2
,
将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于(??
)
A.?39°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?51°
3.如图所示,一辆汽车经过一段公路两次拐弯后,和原来的行驶方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于142°,第二次拐的角∠C的度数为
(???
)
A.?38°?????????????????????????????????????B.?142°?????????????????????????????????????C.?130°?????????????????????????????????????D.?140°
4.下列四个图中,
一定成立的是(?????
)
A.????????????????????B.????????????????????C.????????????????????D.?
5.如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为(???
)
A.?55°??????????????????????????????????????B.?50°??????????????????????????????????????C.?45”??????????????????????????????????????D.?40°
6.如图,直线
,折线
交
于M,交
于N,点F在
与
之间,设
,
,则
的度数是
?????
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
7.如图,直线
∥
,将一块含
角的直角三角尺按图中方式放置,其中点A和点B两点分别落在直线a和b???
上.若
,则
的度数为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
8.如图,
中,∠ACB=90°,DE
过点C
,
且DE∥AB,若∠ACD=65°,则∠B的度数是(???
)
A.?25°???????????????????????????????????????B.?35°???????????????????????????????????????C.?45°???????????????????????????????????????D.?55°
9.已知a,b,c是三条直线,下列结论正确的是(???
)
A.?若a∥b,b∥c,则a∥c?????????????????????????????????????????B.?若a⊥b,b⊥c,则a⊥c
C.?若a∥b,b⊥c,则a∥c????????????????????????????????????????D.?若a⊥b,b∥c,则a∥c
10.如图所示,∠A0B
=
40°,OC平分∠AOB,直尺与OC垂直,则∠1等于(??
)
A.?60°???????????????????????????????????????B.?70°???????????????????????????????????????C.?50°???????????????????????????????????????D.?40°
11.如图,
,
,则
,
,
之间的关系是(???
)
A.?
B.?
C.?
D.?
12.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是(??
)
A.?①②③??????????????????????????B.?①②④??????????????????????????C.?①③④??????????????????????????D.?①②③④???????
图4
二、填空题
13.如图,∠1=∠2,∠A=70°,则∠ADC=________度;
14.如图,
中,
是
上一点,
是
上一点,
,
,
,则
________.
15.如图CD⊥AB于D,EF⊥AB于F,∠DGC=105°,∠BCG=75°,则∠1+∠2=________.
16.如图,已知AE//CD,BC⊥CD于C,若∠A=28°,则∠ABC=________
17.如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=________.
?
18.已知∠A与∠B(
,
)的两边-边平行,另一边互相垂直,且
,则∠A的度数为________°.
三、解答题
19.如图已知AB//CD,试探究∠A,∠APC,∠C的数量关系.
?
20.如图,已知AB∥CD,CD∥EF,
∠A=105°,
∠ACE=51°.求
∠E.
21.如图,已知AB∥CD∥EF,PS
⊥
GH交GH于P.在
∠FRG=110°时,求
∠PSQ.
22.如图,已知直线l1∥l2
,
l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
?
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系
参考答案
1.
B
2.
D
3.
B
4.
B
5.
A
6.
D
7.
A
8.
A
9.
A
10.
B
11.
C
12.
D
13.
110
14.
40
15.
180°
16.
118
17.
154°
18.
36或96
19.
解:(1)作
,如图所示,
,
,
∴
,
∴
.
;(2)延长CP交AB于点N,
,
,
∴
,
∴
,
∴
.
20.解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=105°,
∴∠ACD=75°,
又∵∠ACE=51°,
∴∠DCE=∠ACD-∠ACE=75°-51°=24°,
∵CD∥EF,
∠E=∠DCE=24°.
21.解:∵AB∥EF,
∴∠FRG=∠APR,
∵∠FRG=110°,
∴∠APR=110°,
又∵PS⊥GH,
∴∠SPR=90°,
∴∠APS=∠APR-∠SPR=20°,
∵AB∥CD,
∴∠PSQ=∠APS=20°.
22.
(1)证明:过P作PQ∥l1∥l2
,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)解:
∠3=∠2﹣∠1;
证明:过P作直线PQ∥l1∥l2
,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
?
(3)解:
∠3=360°﹣∠1﹣∠2.
证明:过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
(4)解:
过P作PQ∥l1∥l2;
①当P在C点上方时,
同(2)可证:∠3=∠DFP﹣∠CEP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠DFP﹣∠CEP+∠2﹣∠1=0,
即∠3=∠1﹣∠2.
②当P在D点下方时,
∠3=∠2﹣∠1,解法同上.
综上可知:当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.
?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
